时间序列预测 — LSTM实现多变量多步负荷预测(Tensorflow):多输入多输出
?专栏链接:https://blog.csdn.net/qq_41921826/category_12495091.html
专栏内容
?所有文章提供源代码、数据集、效果可视化
?文章多次上领域内容榜、每日必看榜单、全站综合热榜
时间序列预测存在的问题
?现有的大量方法没有真正的预测未来值,只是用历史数据做验证
?利用时间序列分解算法存在信息泄露的问题:有人用emd+lstm对时间序列进行预测,是否存在原理上的问题? - 知乎
目录
1?数据处理
1.1 导入库文件
import time
import datetime
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sampen import sampen2 # sampen库用于计算样本熵
from vmdpy import VMD # VMD分解库
from itertools import cycle
import tensorflow as tf
from sklearn.cluster import KMeans
from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error, mean_absolute_percentage_error
from sklearn.preprocessing import MinMaxScaler
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Activation, Dropout, LSTM, GRU, Reshape, BatchNormalization
from tensorflow.keras.callbacks import ReduceLROnPlateau, EarlyStopping, ModelCheckpoint
from tensorflow.keras.optimizers import Adam
# 忽略警告信息
import warnings
warnings.filterwarnings('ignore')) plt.rcParams['font.sans-serif'] = ['SimHei'] # 显示中文
plt.rcParams['axes.unicode_minus'] = False # 显示负号
plt.rcParams.update({'font.size':18}) #统一字体字号1.2 导入数据集
实验数据集采用数据集6:澳大利亚电力负荷与价格预测数据(下载链接),包括数据集包括日期、小时、干球温度、露点温度、湿球温度、湿度、电价、电力负荷特征,时间间隔30min。
from itertools import cycle
# 可视化数据
def visualize_data(data, row, col):
cycol = cycle('bgrcmk')
cols = list(data.columns)
fig, axes = plt.subplots(row, col, figsize=(16, 4))
fig.tight_layout()
if row == 1 and col == 1: # 处理只有1行1列的情况
axes = [axes] # 转换为列表,方便统一处理
for i, ax in enumerate(axes.flat):
if i < len(cols):
ax.plot(data.iloc[:,i], c=next(cycol))
ax.set_title(cols[i])
else:
ax.axis('off') # 如果数据列数小于子图数量,关闭多余的子图
plt.subplots_adjust(hspace=0.6)
plt.show()
visualize_data(data_raw.iloc[:,2:], 2, 3)
?
单独查看部分负荷数据,发现有较强的规律性。
?
?1.3 缺失值分析
首先查看数据的信息,发现并没有缺失值
data_raw.info()
进一步统计缺失值
data_raw.isnull().sum()
2 构造训练数据
构造数据前先将数据变为数值类型
data_load = data_raw.iloc[:,2:].values构造训练数据,也是真正预测未来的关键。首先设置预测的timesteps时间步、predict_steps预测的步长(预测的步长应该比总的预测步长小),length总的预测步长,参数可以根据需要更改。
timesteps = 48*7 #构造x,为72个数据,表示每次用前72个数据作为一段
predict_steps = 6 #构造y,为12个数据,表示用后12个数据作为一段
length = 48 #预测多步,预测96个数据,每次预测96个,想想要怎么构造预测才能满足96?
feature_num = 6 #特征个数通过前timesteps行历史数据预测后面predict_steps个数据,需要对数据集进行滚动划分(也就是前timesteps行的数据和后predict_steps行的数据训练,后面预测时就可通过timesteps行数据预测未来的predict_steps行数据)。这里需要注意的是,因为是多变量预测多变量,特征就是标签(例如,前5行[干球温度、露点温度、湿球温度、电价、电力负荷]预测第6行[干球温度、露点温度、湿球温度、电价、电力负荷],划分数据集时,就用前5行当做train_x,第6行作为train_y,此时的train_y有多列,而不是只有1列)。
# 构造数据集,用于真正预测未来数据
# 整体的思路也就是,前面通过前timesteps个数据训练后面的predict_steps个未来数据
# 预测时取出前timesteps个数据预测未来的predict_steps个未来数据。
def create_dataset(datasetx, datasety=None, timesteps=96*7, predict_size=12):
datax = [] # 构造x
datay = [] # 构造y
for each in range(len(datasetx) - timesteps - predict_size):
x = datasetx[each:each + timesteps]
# 判断是否是单变量分解还是多变量分解
if datasety is not None:
y = datasety[each + timesteps:each + timesteps + predict_size]
else:
y = datasetx[each + timesteps:each + timesteps + predict_size]
datax.append(x)
datay.append(y)
return datax, datay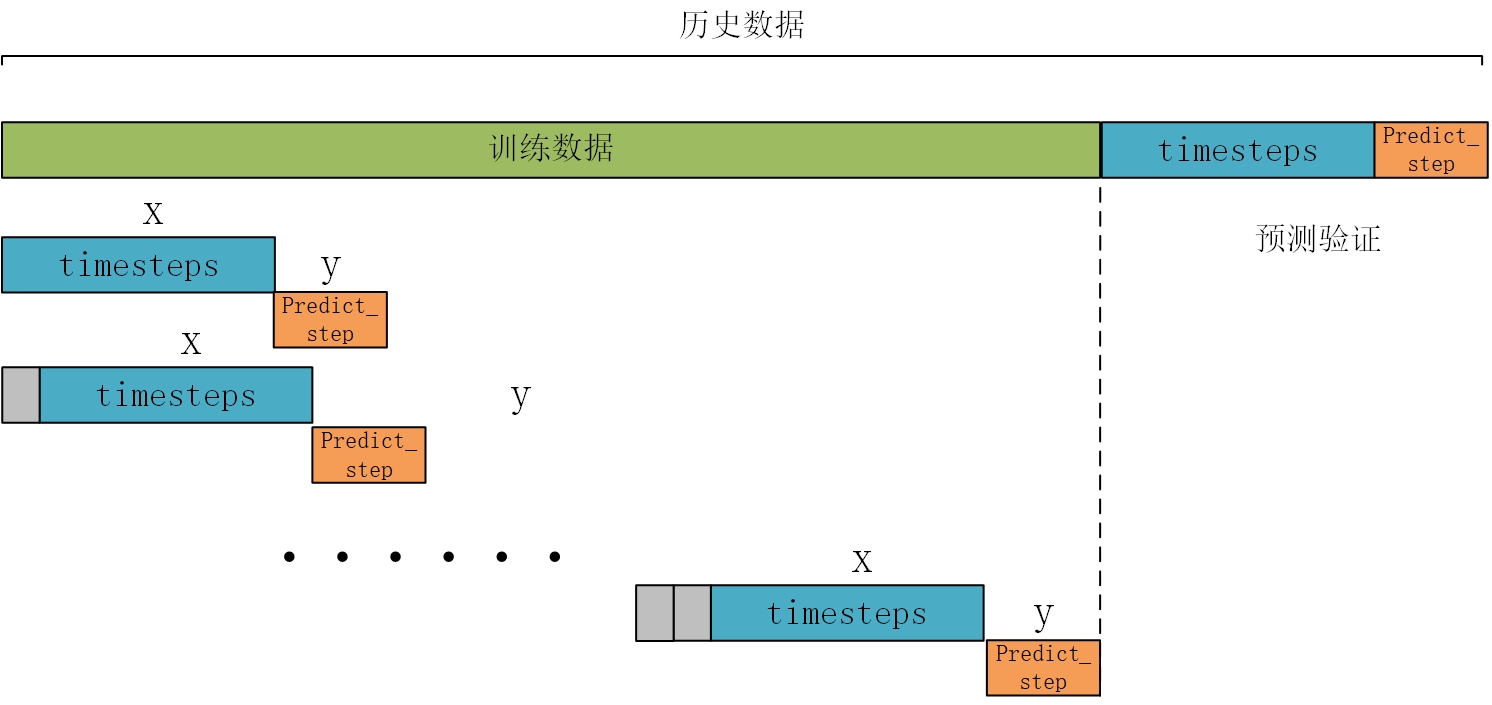
?数据处理前,需要对数据进行归一化,按照上面的方法划分数据,这里返回划分的数据和归一化模型(变量和多变量的归一化不同,多变量归一化需要将X和Y分开归一化,不然会出现信息泄露的问题),此时的归一化相当于是单变量归一化,函数的定义如下:
# 数据归一化操作
def data_scaler(datax, datay=None, timesteps=36, predict_steps=6):
# 数据归一化操作
scaler1 = MinMaxScaler(feature_range=(0, 1))
datax = scaler1.fit_transform(datax)
# 用前面的数据进行训练,留最后的数据进行预测
# 判断是否是单变量分解还是多变量分解
if datay is not None:
scaler2 = MinMaxScaler(feature_range=(0, 1))
datay = scaler2.fit_transform(datay)
trainx, trainy = create_dataset(datax, datay, timesteps, predict_steps)
trainx = np.array(trainx)
trainy = np.array(trainy)
return trainx, trainy, scaler1, scaler2
else:
trainx, trainy = create_dataset(datax, timesteps=timesteps, predict_size=predict_steps)
trainx = np.array(trainx)
trainy = np.array(trainy)
return trainx, trainy, scaler1, None然后分解的数据进行划分和归一化。通过前7天的48*7行数据预测后1天的数据48个,需要对数据集进行滚动划分(也就是前48*7行的数据和后6行的数据训练,后面预测时就可通过48*7行数据测未来的6行标签,然后将6行预测值添加到历史数据中,历史数据变为48*7+6个,再取出后48*7行数据进行预测,得到6行预测值,滚动进行预测直到预测完成,注意此时的预测值是行而不是个)
trainx, trainy, scalerx, scalery = data_scaler(data_load, timesteps=timesteps, predict_steps=predict_steps)?
3 LSTM模型训练
首先划分训练集、测试集、验证数据:
train_x = trainx[:int(trainx.shape[0] * 0.8)]
train_y = trainy[:int(trainy.shape[0] * 0.8)]
test_x = trainx[int(trainx.shape[0] * 0.8):]
test_y = trainy[int(trainy.shape[0] * 0.8):]
test_x.shape, test_y.shape, train_x.shape, train_y.shape首先搭建模型的常规操作,然后使用训练数据trainx和trainy进行训练,进行50个epochs的训练,每个batch包含64个样本(建议使用GPU进行训练)。
# 搭建LSTM训练函数
def LSTM_model_train(trainx, trainy, valx, valy, timesteps, predict_steps):
# 调用GPU加速
gpus = tf.config.experimental.list_physical_devices(device_type='GPU')
for gpu in gpus:
tf.config.experimental.set_memory_growth(gpu, True)
# 搭建LSTM模型
start_time = datetime.datetime.now()
model = Sequential()
model.add(LSTM(128, input_shape=(timesteps, trainx.shape[2]), return_sequences=True))
model.add(BatchNormalization()) # 添加BatchNormalization层
model.add(Dropout(0.2))
model.add(LSTM(64, return_sequences=False))
model.add(Dense(predict_steps * trainy.shape[2]))
model.add(Reshape((predict_steps, trainy.shape[2])))
# 使用自定义的Adam优化器
opt = Adam(learning_rate=0.001)
model.compile(loss="mean_squared_error", optimizer=opt)
# 添加早停和模型保存的回调函数
es = EarlyStopping(monitor='val_loss', mode='min', verbose=1, patience=10)
mc = ModelCheckpoint('best_model.h5', monitor='val_loss', mode='min', save_best_only=True)
# 训练模型,这里我假设你有一个验证集(valx, valy)
history = model.fit(trainx, trainy, validation_data=(valx, valy), epochs=50, batch_size=64, callbacks=[es, mc])
# 记录训练损失
loss_history = history.history['loss']
end_time = datetime.datetime.now()
running_time = end_time - start_time
return model, loss_history, running_time然后进行训练,将训练的模型、损失和训练时间保存。
#模型训练
model, loss_history, running_time = LSTM_model_train(train_x, train_y, test_x, test_y, timesteps, predict_steps)
# 将模型保存为文件
model.save('lstm_model.h5')训练损失可视化
plt.figure(dpi=100, figsize=(14, 5))
plt.plot(loss_history, markevery=5)
4 LSTM模型预测
4.1 分量预测
下面介绍文章中最重要,也是真正没有未来特征的情况下预测未来标签的方法。整体的思路也就是取出预测前48*7行数据预测未来的6行数据,然后见6行数据添加进历史数据,再预测6行数据,滚动预测。因为每次只能预测6行数据,但是我要预测48个数据,所以采用的就是循环预测的思路。每次预测的6行数据,添加到数据集中充当预测x,然后在预测新的6行y,再添加到预测x列表中,如此往复,最终预测出48行。(注意多变量预测多变量预测的是多列,预测单变量只有一列)
# #滚动predict
# #因为每次只能预测6个数据,但是我要预测6个数据,所以采用的就是循环预测的思路。
# #每次预测的6个数据,添加到数据集中充当预测x,然后在预测新的6个y,再添加到预测x列表中,如此往复,最终预测出48个点。
def predict_using_LSTM(model, data, timesteps, predict_steps, feature_num, length, scaler):
predict_xlist = np.array(data).reshape(1, timesteps, feature_num)
predict_y = np.array([]).reshape(0, feature_num) # 初始化为空的二维数组
print('predict_xlist', predict_xlist.shape)
while len(predict_y) < length:
# 从最新的predict_xlist取出timesteps个数据,预测新的predict_steps个数据
predictx = predict_xlist[:,-timesteps:,:]
# 变换格式,适应LSTM模型
predictx = np.reshape(predictx, (1, timesteps, feature_num))
print('predictx.shape', predictx.shape)
# 预测新值
lstm_predict = model.predict(predictx)
print('lstm_predict.shape', lstm_predict.shape)
# 滚动预测
# 将新预测出来的predict_steps个数据,加入predict_xlist列表,用于下次预测
print('predict_xlist.shape', predict_xlist.shape)
predict_xlist = np.concatenate((predict_xlist, lstm_predict), axis=1)
print('predict_xlist.shape', predict_xlist.shape)
# 预测的结果y,每次预测的6行数据,添加进去,直到预测length个为止
lstm_predict = scaler.inverse_transform(lstm_predict.reshape(predict_steps, feature_num))
predict_y = np.concatenate((predict_y, lstm_predict), axis=0)
print('predict_y', predict_y.shape)
return predict_y然后对数据进行预测,得到预测结果。
from tensorflow.keras.models import load_model
model = load_model('best_model.h5')
pre_x = scalerx.fit_transform(data_load[-48*8:-48])
pre_y = data_load[-48:,-1]
y_predict = predict_using_LSTM(model, pre_x, timesteps, predict_steps, feature_num, length, scalerx)4.2 可视化
对预测的结果进行可视化并计算误差。
# 预测并计算误差和可视化
def error_and_plot(y_true,y_predict):
# 计算误差
r2 = r2_score(y_true, y_predict)
rmse = mean_squared_error(y_true, y_predict, squared=False)
mae = mean_absolute_error(y_true, y_predict)
mape = mean_absolute_percentage_error(y_true, y_predict)
print("r2: %.2f\nrmse: %.2f\nmae: %.2f\nmape: %.2f" % (r2, rmse, mae, mape))
# 预测结果可视化
cycol = cycle('bgrcmk')
plt.figure(dpi=100, figsize=(14, 5))
plt.plot(y_true, c=next(cycol), markevery=5)
plt.plot(y_predict, c=next(cycol), markevery=5)
plt.legend(['y_true', 'y_predict'])
plt.xlabel('时间')
plt.ylabel('功率(kW)')
plt.show()
return 0error_and_plot(pre_y, y_predict[:,-1]) 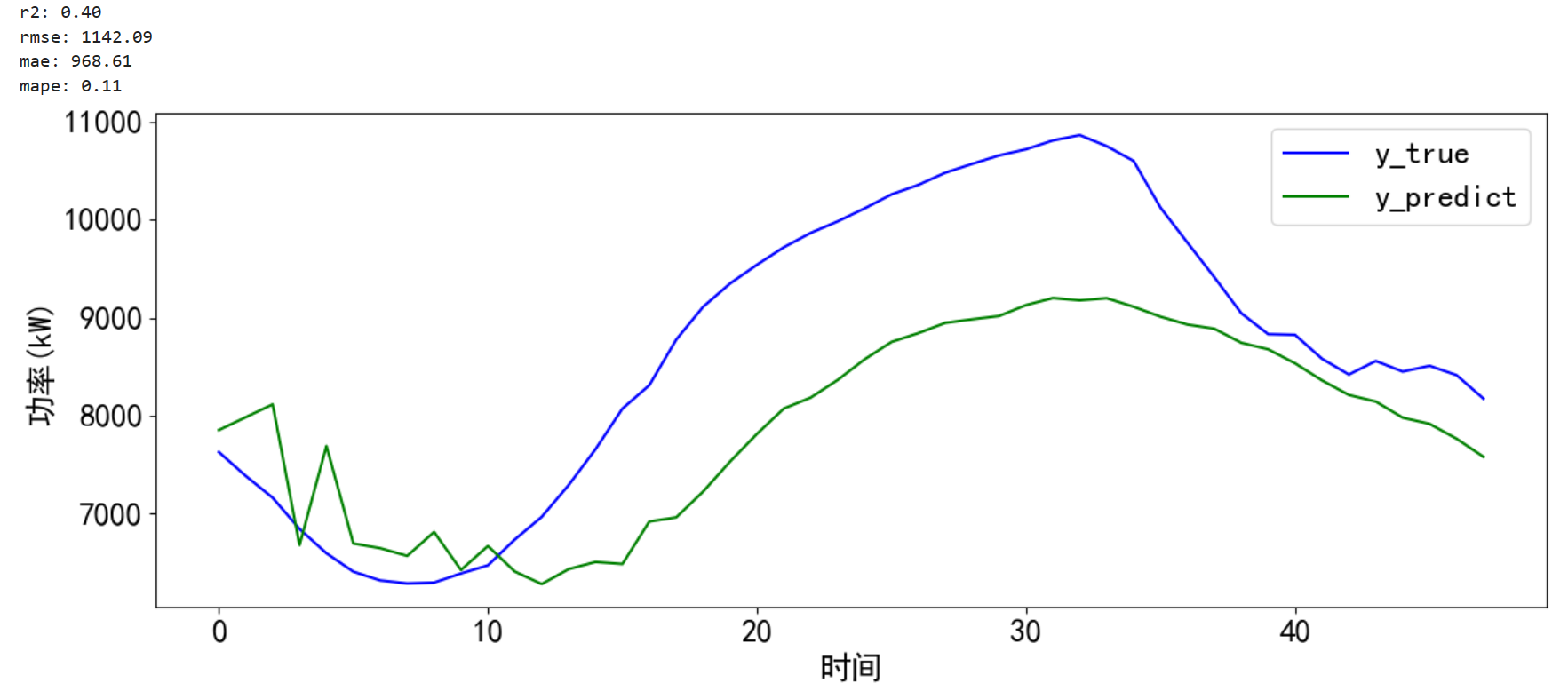
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!






