12.27重构二叉树，插入排序，队列（股票，模拟），后缀表达式求值，括号匹配，验证栈序列，选择题部分

重构二叉树

误

string in, post;
struct node {
    char a;
    node* lchild, * rchild;
    node(char x='\0') :a(x), lchild(nullptr), rchild(nullptr) {}
};
void so(node* r, int il, int ir, int pl, int pr) {
    if (il > ir)return;
    int root;
    for (root = il; root <= ir; root++) {
        if (in[root] == post[pr])break;
    }//找到根节点在中序序列中的位置
    r->a = in[root];
    int lsize = root - il;//只含一个端点，不包含根节点root
    so(r->lchild,il, root - 1, pl, pl + lsize - 1);//左子树
    so(r->rchild,root + 1, ir, pl + lsize, pr - 1);//右子树
}
void pre(node* root) {
    if (!root)return;
    cout << root->a;
    pre(root->lchild);
    pre(root->rchild);
}
cin >> in >> post;
node* root = new node;
so(root, 0, in.length() - 1, 0, in.length() - 1);
pre(root);

一点基本常识，给你一个后序遍历，那么最后一个就是根（如ABCD，则根为D）?

substr与find，由后序与中序

substr返回的是截取后的子串，第一个参数为开始截取的下标，第二个参数为截取的元素个数

find返回下标，

#include <iostream>
#include <vector>
#include <algorithm>
#include<stack>
#include<queue>
#include <map>
#include<string>
#include<cstdio>
using namespace std;
void b(string in, string a) {
    if (in.size() > 0) {//同理对后序，第k个数下标为k-1,那么第k+1个，下标为k的数，是右子树的第一个数
        char ch = a[a.size() - 1];//从0截取k个，那么最后一个的下标就是k-1,对于中序而言，下标为k的是第k+1个数，是根节点，那么右子树第一个为k+2,下标为k-1
        cout << ch;//如果没有第二个参数，就默认从这个起点截取到末尾
        int k = in.find(ch);//substr第一个参数是截取的起点，第二个参数是截取元素的个数，第二个参数不是截取的终点
        b(in.substr(0, k), a.substr(0, k));//find返回的是下标，恰好就是左子树里的元素个数
        b(in.substr(k + 1), a.substr(k, in.size() - 1 - k));//k代表的恰好是左子树里的元素个数，整个数量由一个根节点，左右子树大小构成，所以右子树大小就是减去
    }
}
int main() {
    string in, a;
    cin >> in >> a;
    b(in, a);
    return 0;
}

由中序与先序——?P1827 [USACO3.4] 美国血统 American Heritage

void so(string in, string pre) {
    if (in.size() < 1)return;
    char ch = pre[0];
    int index = in.find(ch);//index代表根节点在中序序列中的下标位置，恰好代表左子树大小,因为左子树的最后一个元素下标为index-1,中有元素数量为index-1+1
    so(in.substr(0, index), pre.substr(1, index));//左子树
    so(in.substr(index + 1, in.size() - 1 - index), pre.substr(index + 1, in.size() - 1 - index));//右子树
    cout << ch;
}//先序为根左右，中序为左根右
string in, pre;
cin >> in >> pre;
so(in, pre);

s.find(c);
//在字符串s中查找第一个字符c的位置，返回下标，如果没有返回string::npos

s.erase(it);
//在字符串中删除指针it所指向的字符

s.begin();
//返回s的首字符的指针（迭代器）

void b(string in, string a) {
    if (in.size() > 0) {
        char ch = a[a.size() - 1];
        cout << ch;//中序为左根右，后序为左右根
        int k = in.find(ch);//在中序里找根节点的下标,也代表左子树的大小
        b(in.substr(0, k), a.substr(0, k));//左子树
        b(in.substr(k + 1), a.substr(1, in.size() - 1 - k));//0是左子树的第一个元素，那么加上左子树大小，指向的是左子树后的第一个元素，即根节点，而不是左子树的最后一个元素，所以要加个1才是右子树的第一个元素
    }
}
void so(string in, string pre) {
    if (in.size() > 0) {
        char ch = pre[0];
        int index = in.find(ch);
        so(in.substr(0, index), pre(1, index));//截取第二个参数个元素，从节点开始，所以是不包含右端点的
        so(in.substr(index + 1, in.size() - 1 - index), pre.substr(1 + index, in.size() - 1 - index));
        cout << ch;
    }
}

另一种风格?

前序和后序构建

必要条件为左右子树里都得有元素或者都没有，如果孩子里只有一个元素，因为前序后序的左右孩子都在根节点的一侧，所以就无法区分出这个孩子到底是左孩子还是右孩子，就会产生两种情况，有多少个只有一个孩子的情况，就会有1<<n的情况。即有多少个度为1的节点，就会有1<<n的情况

如果每个节点都有左右孩子或者没有，就不会有其它的情况，情况就是唯一的

重构二叉树干的就几件事，第一件是确定本层的节点，本层的根节点；然后划分出左右子树区间，递归解决

int nfind(char* inorder, int size, char v) {
    for (int i = 0; i < size; i++) {
        if (inorder[i] == v)return i;
    }
}
node* build(char* preorder, char* inorder, int size) {//用char*的话，就是数组，只传数组名，即首个元素的下标接口
    if (!size)return nullptr;
    char rd = preorder[0];
    int leftsize = nfind(inorder, size, rd);
    node* root = new node(rd);
    root->lchild = build(preorder + 1, inorder, leftsize);
    root->rchild = build(preorder + 1 + leftsize, inorder + 1 + leftsize, size - 1 - leftsize);
    return root;
}
node* buildpre(char* inorder, char* postorder, int size) {
    if (!size)return nullptr;
    char rd = postorder[size - 1];
    int leftsize = nfind(inorder, size, rd);
    node* root = new node(rd);
    root->lchild = buildpre(inorder, postorder, leftsize);//加上的数代表差距，从头位置加上左子树的大小，那么最后指向的恰好是左子树后的第一个数，而不是左子树的最后一个数，因为起点不是0，而是1，是左子树里的第一个数
    root->rchild = buildpre(inorder + 1 + leftsize, postorder + leftsize, size - 1 - leftsize);
    return root;
}
node* buildin(char* preorder, char* postorder, int size) {
    if (!size)return nullptr;
    char rd = preorder[0];
    node* root = new node(rd);//其它不用特判，因为可以构建出度为1的节点
    if (size == 1)return root;//由于为满二叉树，此时每个序列要么为叶子节点，要么为出度为2的节点，这里检测前一种情况，即此时序列被拆的都只剩一个元素,不然序列里根本就不存后面的元素
    int leftsize = nfind(postorder, size, preorder[1]);//由于根节点的位置在前序后序里的位置都是确定的，所以去找左子树的根节点
    root->lchild = buildin(preorder + 1, postorder, leftsize);
    root->rchild = buildin(preorder + 1 + leftsize, postorder, size - 1 - leftsize);//这里前一个参数要加1才是右子树的起点，因为要越过根节点和左子树，起点为左子树第一个元素，只加左子树大小时，指向根节点位置，再加1才是右子树的第一个元素位置
    return root;//这里第一个为根节点，不是左子树的第一个元素，所以加完后指向的是左子树的最后一个元素，再加1就是右子树的第一个元素
}

TreeNode* buildTree(vector<int>& preorder, vector<int>& postorder, int preStart, int preEnd, int postStart, int postEnd) {
    // 递归终止条件
    if (preStart > preEnd) {
        return nullptr;
    }
    
    // 创建当前节点
    TreeNode* root = new TreeNode(preorder[preStart]);
    
    // 在后序序列中找到当前节点的位置
    int index = postStart;
    while (postorder[index] != preorder[preStart]) {
        index++;
    }
    
    // 计算左子树的节点个数
    int leftCount = index - postStart;
    
    // 构建左子树
    root->left = buildTree(preorder, postorder, preStart + 1, preStart + leftCount, postStart, index - 1);
    
    // 构建右子树
    root->right = buildTree(preorder, postorder, preStart + leftCount + 1, preEnd, index, postEnd - 1);
    
    return root;
}

TreeNode* buildTree(vector<int>& preorder, vector<int>& postorder) {
    int preStart = 0;
    int preEnd = preorder.size() - 1;
    int postStart = 0;
    int postEnd = postorder.size() - 1;
    
    return buildTree(preorder, postorder, preStart, preEnd, postStart, postEnd);
}

层序重构树

void level(node*& t) {
    queue<node*>q;
    int x;
    cin >> x;
    if (!x)return;
    node* t = new node(x);
    q.push(t);
    while (!q.empty()) {
        node* cur = q.front();
        q.pop();
        cin >> x;
        if (x) {
            cur->lchild = new node(x);
            q.push(cur->lchild);
        }
        cin >> x;
        if (x) {
            cur->rchild = new node(x);
            q.push(cur->rchild);
        }
    }
}
void create(node& tree) {
    char t;
    cin >> t;
    if (t == '#') { tree = nullptr; }
    else {
        tree = new node;
        tree->data = t;
        create(tree->lchild);
        create(tree->rchild);
    }
}

?P3884 [JLOI2009] 二叉树问题

这个距离，就是说先向上找最近公共祖先，找的路径乘2，然后找到公共祖先再下来，就不用乘2

#include<bits/stdc++.h>

排序

插入排序

    for (int i = 2; i <= n; i++) {
        int temp = arr[i], j;
        for ( j = i - 1; arr[j] > temp && j >= 1; j--) {
            arr[j + 1] = arr[j];//向后移动这张牌
        }
        arr[j + 1] = temp;
    }

    for (int i = 2; i <= n; i++) {
        int temp = arr[i], j;
        for (j = i - 1; arr[j] > temp && j >= 1; j--) {//j代表的是此时比对的位置，从插入的牌的后面第一个开始
            arr[j + 1] = arr[j];//向后移动这张牌
        }//由于终止时要么不满足j<1,要么不满足arr[j]>temp,即arr[j]<temp或者已越界，所以此时j所指的是这张牌应在的后一个位置
        arr[j + 1] = temp;//此一步比这张牌小，后一步就比这张牌大,但是后一步的牌已经覆盖住了后后一步，所以直接覆盖掉它即可
    }//主要就是因为此时j指向的是，要么比它小的牌，要么越界的第一个，后一步是一定比这张牌大的，所以可以直接赋给下一个指针

归并排序

快速排序

?冒泡排序就是在一个序列当中，从起点开始，不断地往后冒泡交换，每次迭代确定一个最大值，随着冒泡次数的增多，然后最大值确定的也越来越多，需要相邻交换的次数越来越少

即外层循环n次，内层循环n-i次，整体是个n^2的复杂度

选择排序是从0开始保证序列的有序性，每次扩张序列的后一个数，然后和序列的最后一个数作比较，如果比序列的最后一个数大，那么就直接放着；不然，就往前移动，直到前一个数比它小，后一个数比它大，这个数就在有序序列中找到了自己的位置。

队列

7-1 模拟队列 分数 15

要么直接用queue,要么用数组模拟，用数组的话，一个指针表示队头指针，一个指针表示队尾，添加元素时，队尾增加，所以队尾指针增加；出队时，队头出，队头指针++

int p = 1, l = 0;
void push(int num) {
    q[++l] = num;
}
void pop() {
    p++;
}
bool empty() {
    if (l >= p) {
        return false;
    }
    else {
        return true;
    }
}
int query() {
    return q[p];
}

7-3 大師と仙人との奇遇 分数 20

就是队列里记录已经加入的每支股票的价格，然后先比较队头，直到队列为空或者不大于今天的价格就停止，操作完成后再入队今天的

    priority_queue<int, vector<int>, greater<int>>q;
    int n, num, ans = 0;
    cin >> n;
    for (int i = 1; i < n; i++) {
        cin >> num;
        if (q.empty()) {
            q.push(num);
        }
        else {
            while (!q.empty() && q.top() < num) {
                ans += (num - q.top());
                q.pop();
            }
            q.push(num);
        }
    }
    cin >> num;
    while (!q.empty()) {
        int cur = q.top();
        q.pop();
        ans += (num - cur);
    }

    priority_queue<int, vector<int>, greater<int>>q;
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> num;
        int cnt = 0;
        if (i != n) {
            while (!q.empty()) {
                if (num > q.top()) {
                    q.pop();
                    cnt++;
                }
                else {
                    break;
                }
            }
        }
        else {
            cnt = q.size();
        }
        pin += cnt * num;
        if (i != n) {
            pout += num;
            q.push(num);
        }
    }
    cout << pin - pout << endl;

?

线性表、链表

7-2 后缀表达式求值

    string s1;
    stack<int>s;
    int sum, top = 0, num1, num2;
    getline(cin, s1);//getline函数可以保证输入空格时不中断
    for (int i = 0; s1[i] != '#'; i++) {
        if (s1[i] >= '0' && s1[i] <= '9') {
            sum = s1[i] - '0';//字符数字减去字符0，即可得到正常数字，因为在ASC里是连续的
            int j;
            for (j = i + 1; s1[i] != '#'; j++) {
                if (s1[j] >= '0' && s1[j] <= '9') {
                    sum = sum * 10 + (s1[j] - '0');
                }
                else { break; }
            }
            if (i > 0 && s1[i - 1] == '-') {
                sum = -sum;
            }
            i = j - 1;
            s.push(sum);
            top++;
        }
        else if (s1[i] == ' ') { continue; }
        else if (s1[i] == '-' && s1[i + 1] != ' ') { continue; }
        else {
            if (top < 2) {
                cout << "Expression Error" << s.top() << endl;
                return 0;
            }
            num1 = s.top();
            s.pop();
            top--;
            num2 = s.top();
            s.pop();
            top()--;
            switch (s1[i]) {
            case '+':s.push(num2 + num1); top++; break;
            case'-':s.push(num2 - num1); top++; break;
            case'*':s.push(num2 * num1); top++; break;
            case'/':
                if (num1 == 0) {
                    cout << "Error: " << num2 << "/0" << endl;
                }
                s.push(num2 / num1);
                top++;
                break;
            }
        }
    }
    if (top != 1) {
        cout << "Expression Error: " << s.top() << endl;
    }
    else {
        cout << s.top();
    }

    string s;
    stack<int>st;
    int sum, top = 0, num1, num2;
    getline(cin, s);
    for (int i = 0; s[i] != '#'; i++) {
        if (s[i] >= '0' && s[i] <= '9') {
            sum = s[i] - '0';
            int j;
            for (j = i + 1; s[i] != '#'; j++) {
                if (s[j] >= '0' && s[j] <= '9') {
                    sum = sum * 10 + (s[j] - '0');
                }
                else { break; }
            }
            if (i > 0 && s[i - 1] == '-') {
                sum = -sum;
            }
            i = j - 1;
            st.push(sum);
            top++;
        }
        else if (s[i] == ' ')continue;
        else if (s[i] == '-' && s[i + 1] != ' ')continue;
        else {
            if (top < 2) {
                cout << "E:" << st.top() << endl;
                return 0;
            }
            num1 = st.top();
            st.pop();
            top--;
            num2 = st.top();
            st.pop();
            top--;
            switch (s[i]) {
            case'+':s.push(num2 + num1); top++; break;
            case'-':s.push(num2 - num1); top++; break;
            case'*':s.push(num2 * num1); top++; break;
            case'/':if (num1 == 0) { cout << "E" << num2 << "/0" << endl; return 0; }
                   s.push(num2 / num1);
                   top++;
                   break;
            }
        }
    }
    if (top != 1)cout << "E" << s.top() << endl;
    else cout << s.top();

7-1 字符串匹配问题(strs)

遇到左括号入栈，遇到右括号出栈，

还有就是要注意括号的次序问题，就是把括号

    char a[] = { '{','[','(','<','}',']',')','>' };
    int b[300], n;
    cin >> n;
    while (n--) {
        string s;
        cin >> s;
        stack<int>st;
        bool flag = true;
        for (int i = 0; i < s.size(); i++) {
            for (int j = 0; j < 8; j++) {
                if (s[i] == a[j]) {
                    b[i] = j;
                    break;//就是把原来的括号字符串转换为B里的数字数组
                }
            }
        }
        for (int i = 0; i < s.size(); i++) {
            if (b[i] <= 3) {
                if (!st.empty() && b[i] < st.top()) {//用数字代表括号的优先次序，那么能不能继续插入，就是看堆顶的元素的编号和此时自己的关系
                    flag = false;//也就是必须要保证一个递增的顺序，不然就不能继续插入
                    break;
                }
                else {
                    st.push(b[i]);
                }//正常插入
            }
            else if (b[i] >= 4) {
                if (st.empty() || (st.top() + 4) != b[i]) {
                    flag = false;
                    break;
                }
                else {
                    st.pop();//正常的匹配，删除
                }
            }
        }
        if (!st.empty())cout << "no" << endl;
        else if (flag)cout << "yes" << endl;
        else cout << "no" << endl;
    }

检验栈序列

    cin >> q;
    while (q--) {
        cin >> n;
        stack<int>s;
        int cnt = 1;
        for (int i = 1; i <= n; i++)cin >> push[i];
        for (int i = 1; i <= n; i++)cin >> pop[i];
        for (int i = 1; i <= n; i++) {
            s.push(push[i]);//先入
            while (!s.empty() && s.top() == pop[cnt]) {//然后一直出队列，要求队列不空而且栈顶元素和Pop此时指向元素相同
                s.pop();
                cnt++;
            }
        }
        if (s.empty())cout << "Yes" << endl;
        else cout << "No" << endl;
    }

6-2 寻找链表元素的前驱结点

ptr pre(ptr h,int x){
    ptr res=new node();
    if(h==nullptr||h->data==x){return NULL;}
    else{
        res->next=h;
        while(h!=NULL){
            if(h->data==x){return res;}
            res=h;
            h=h->next;
        }
    }
    return NULL;
    /*if(h==NULL){return nullptr;}else{
        return res;
    }*/
  
}

线性表删除

List Delete( List &L, ElementType minD, ElementType maxD ){
        int left=0;
    int length=L.last;
        for(int i=0;i<=length;i++){
            if(L.Data[i]<minD||L.Data[i]>maxD){
                //L.last--;
                continue;//这样就表示删掉了
            }
            L.Data[left++]=L.Data[i];
        }
    L.last=left;
    return L;
}

栈?

7-3 胡同

    cin >> t;
    while (t--) {
        cin >> n;
        for (int i = 1; i <= n; i++)cin >> a[i];
        for (int i = 1; i <= n; i++)cin >> b[i];
        stack<int>st;
        int cnt = 1;
        for (int i = 1; i <= n; i++) {
            st.push(a[i]);
            while (!st.empty() && st.top() == b[cnt]) {
                st.pop();
                cnt++;
            }
        }
        if (st.empty())cout << "yes";
        else cout << "no";
    }

括弧匹配，弱化版

    string s;
    stack<char>ch;
    bool flag = true;
    cin >> s;
    for (int i = 0; i < s.length(); i++) {
        if (s[i] == '(')ch.push(')');
        if (s[i] == '[')ch.push(']');
        if (s[i] == ']') {
            if (ch.empty()||ch.top()!=']') {
                flag = false;
                break;
            }
            else {
                ch.pop();
            }
        }
        if (s[i] == ')') {
            if (ch.empty() || ch.top() != ')') {
                flag = false;
                break;
            }
            else {
                ch.pop();
            }
        }
    }
    if (ch.empty() && flag) { cout << "ok" << endl; }
    else {
        cout << "no" << endl;
    }

选择题复习

Ologn

看重复执行次数，为1+2+4+……+n，那么最后就是等比数列求和，N可以被视为2的指数次，用等比求和公式算，算完是On的复杂度

链表结点定义为(data,next},在P指向的结点之后插入结点S的代码是?S->next=P->next; P->next=S;

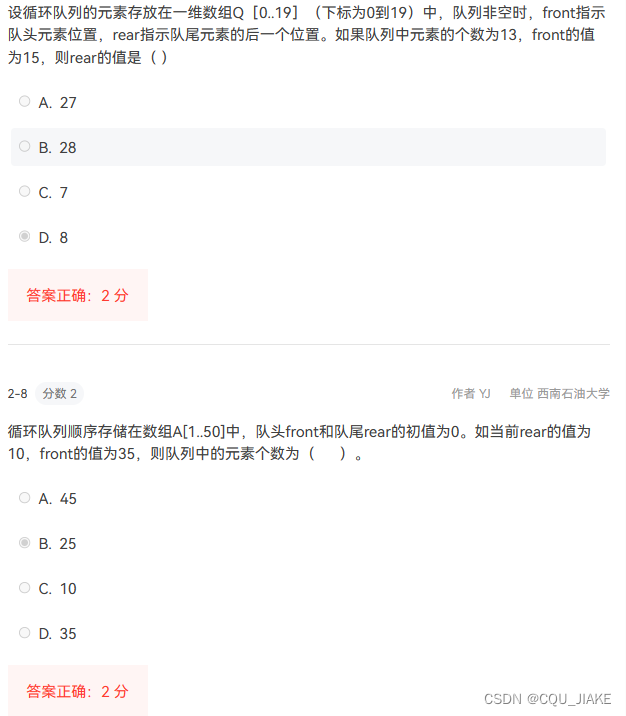
即遍历一次数组，但不需要做任何操作