数据结构学习笔记（六）集合

---

1. 前言

本系列笔记基于 清华大学出版社的《数据结构：用面向对象方法与C++语言描述》第二版进行学习。

2. 概念

集合是成员的一个群集，集合中成员可以是原子（单元素）也可以是集合。集合的成员必须是互不相同的，即同一个成员不能在集合中出现多次。

2.1 位向量实现集合抽象数据类型

文字有点抽象，大概就是用二进位（0，1）数组来实现集合。

还是看代码吧。。太抽象了！

并：两个中有一个是1就是1
交：两个中都是1才是1
差：在第一个是1，第二个没有的就是1

#include <iostream>
#include<assert.h>

using namespace std;

const int DefaultSize = 50;

class bitSet {
public:
    bitSet(int sz = DefaultSize);
    bitSet(const bitSet& R);
    ~bitSet() { delete[] bitVector; }
    void makeEmpty() {
        for (int i = 0; i < vectorSize; i++) bitVector[i] = 0;
    }
    int getMember(const int x);     // 读取集合元素x
    void putMember(const int x, int v);  // 将v赋给集合元素x
    bool addMember(const int x);        // 加入新成员x
    bool delMember(const int x);         // 删除老成员x
    bitSet& operator = (const bitSet& R);   // 将集合R赋给集合this
    bitSet operator+(const bitSet& R);         // 集合的并运算
    bitSet operator*(const bitSet& R);          //集合的交运算
    bitSet operator-(const bitSet& R);          // 集合的差运算
    bool Contains(const int x);                     // 判断x是否是集合中元素
    bool subSet(bitSet& R);                         // 判断this是否是R的子集
    bool operator == (bitSet& R);               // 判断集合this与R是否相等
    friend istream& operator>>(istream& in, bitSet& R);
    friend ostream& operator<<(ostream& out, bitSet& R);
private:
    int setSize;                    // 集合大小
    int vectorSize;               // 位数组大小
    unsigned short* bitVector;     // 存储元素的位数组
};

bitSet::bitSet(int sz) :setSize(sz) {
    assert(setSize > 0);
    vectorSize = (setSize + 15) >> 4;           // 存储数组大小
    bitVector = new  unsigned short[vectorSize];             // 
    assert(bitVector != NULL);
    for (int i = 0; i < vectorSize; i++)
        bitVector[i] = 0;
}

bitSet::bitSet(const bitSet& R)
{
    setSize = R.setSize;
    vectorSize = R.vectorSize;
    bitVector = new unsigned short[vectorSize];
    assert(bitVector != NULL);
    for (int i = 0; i < vectorSize; i++) {
        bitVector[i] = R.bitVector[i];
    }

}

int bitSet::getMember(const int x)
{
    int ad = x / 16;
    int id = x % 16;
    unsigned short elem = bitVector[ad];                        // 取x所在的数组元素
    return int((elem >> (15 - id) & 1));                             // 取第id位的值            
}

void bitSet::putMember(const int x, int v)
{
    int ad = x / 16;
    int id = x % 16;
    unsigned short elem = bitVector[ad];
    unsigned short temp = elem >> (15 - id);                  //    右移至末尾
    elem = elem << (id + 1);                                            
    if (temp % 2 == 0 && v == 1) temp = temp + 1;       // 根据V的值修改该位
    else if (temp % 2 == 1 && v == 0) temp = temp - 1;
    bitVector[ad] = (temp << (15 - id)) || (elem >> (id + 1));      // 送回
}

bool bitSet::addMember(const int x)
{
    assert(x >= 0 && x < setSize);                      // 检查x的合理性
    if (getMember(x) == 0) {
        putMember(x, 1); 
        return true;
    }
    return false;
}

bool bitSet::delMember(const int x)
{
    assert(x >= 0 && x < setSize);
    if (getMember(x) == 1) { putMember(x, 0); return true; }
    return false;
}

bitSet bitSet::operator+(const bitSet& R)
{
    assert(vectorSize == R.vectorSize);
    bitSet temp(vectorSize);
    for (int i = 0; i < vectorSize; i++) {
        temp.bitVector[i] = bitVector[i] | R.bitVector[i];
        return temp;
    }
}

bitSet bitSet::operator*(const bitSet& R)
{
    assert(vectorSize == R.vectorSize);
    bitSet temp(vectorSize);
    for (int i = 0; i < vectorSize; i++)
        temp.bitVector[i] = bitVector[i] & R.bitVector[i];
    return temp;
}

bitSet bitSet::operator-(const bitSet& R)
{
    assert(vectorSize == R.vectorSize);
    bitSet temp(vectorSize);
    for (int i = 0; i < vectorSize; i++)
        temp.bitVector[i] = bitVector[i] & !R.bitVector[i];
    return temp;
}

bool bitSet::Contains(const int x)
{               // 判断x是否是集合中的元素
    assert(x >= 0 && x <= setSize);
    return (getMember(x) == 1) ? true : false;
}

bool bitSet::subSet(bitSet& R)
{                                                                   // 判断this是否是R的子集
    assert(setSize == R.setSize);
    for (int i = 0; i < vectorSize; i++)
        if (bitVector[i] && !R.bitVector[i]) return false;          // 如果有一位不相同，则返回false；
    return true;
}

bool bitSet::operator==(bitSet& R)
{
    if (vectorSize != R.vectorSize) return false;
    for (int i = 0; i < vectorSize; i++)
        if (bitVector[i] != R.bitVector[i]) return false;
    return true;
}

2.2 有序链表实现集合的抽象数据类型

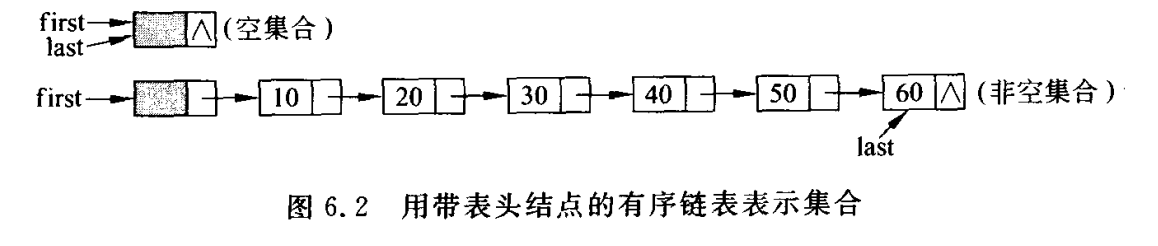
链表中每个结点表示集合的一个成员,各个结点在链表中升序排列.

实现

#include <iostream>

struct SetNode {
    int data;
    SetNode* link;                              // 链接指针
    SetNode() :link(NULL) {};
    SetNode(const int x, SetNode* next = NULL) :data(x), link(next) {};
};

class LinkedSet {
public:
    LinkedSet() { first = last = new SetNode; }             
    LinkedSet(LinkedSet& R);
    ~LinkedSet() { makeEmpty(); delete first; }
    void makeEmpty();
    bool addMember(int& x);                             // 增加x到集合
    bool delMember(int& x);                              // 删去x
    void operator = (LinkedSet& R);       // 赋值R到this
    LinkedSet& operator +(LinkedSet& R);        // this与R的并
    LinkedSet& operator *(LinkedSet& R);        // this与R的交
    LinkedSet& operator -(LinkedSet& R);        // this与R的差
    bool Contains(const int x);                          // 判断x是否是集合的成员
    bool operator==(LinkedSet& R);                 // 判断R是否和this相等
    bool Min(int& x);                                           // 返回最小元素的值
    bool Max(int& x);                                           // 返回最大元素的值
    bool subSet(LinkedSet& R);                          // 判断this是否是R的子集

private:
    SetNode* first, * last;
};

int main() 
{
    std::cout << "Hello World!\n";
}

LinkedSet::LinkedSet(LinkedSet& R)
{
    SetNode* srcptr = R.first->link;                    // 和单链表的复制构造函数一样
    first = last = new SetNode;                             
    while (srcptr != NULL) {
        last->link = new SetNode(srcptr->data);
        last = last->link;
        srcptr = srcptr->link;
    }
    last->link = NULL;
}

bool LinkedSet::addMember(int& x)
{
    // 增加新元素x到集合之中
    SetNode* p = first->link;
    SetNode* pre = first;
    while (p != NULL && p->data < x) {
        pre = p;
        p = p->link;
    }
    while (p != NULL && p->data == x) return false;
    SetNode* s = new SetNode(x);                                    // 创建值位x的结点
    s->link = p;
    pre->link = s;
    if (p == NULL) last = s;
    return false;
}

bool LinkedSet::delMember(int& x)
{
    SetNode* p = first->link;
    SetNode* pre = first;
    while (p != NULL && p->data < x) {
        pre = p;
        p = p->link;
    }
    if (p != NULL && p->data == x) {
        pre->link = p->link;             //前面的结点的指针指向后面的结点
        if (p == last) last = pre;
        delete p;
        return true;
    }
    else return false;
}

void LinkedSet::operator=(LinkedSet& R)
{
    // 复制集合R到this
    
    SetNode* pb = R.first->link;    // 先找到要复制的集合R
    SetNode* pa = first = new SetNode;          // 复制目标集合，创建头结点
    while (pb != NULL) 
    {
        pa->link = new SetNode(pb->data);
        pa = pa->link;
        pb = pb->link;                                                              // 遍历集合
    }
    pa->link = NULL;
    last = pa;
}

LinkedSet& LinkedSet::operator+(LinkedSet& R)
{
    SetNode* pb = R.first->link;                        // R集合的指针
    SetNode* pa = first->link;                          // this集合的指针
    LinkedSet temp;                                         // 存放空结果链表
    SetNode* p, * pc = temp.first;                                                 // 结果链的存放指针
    while (pa != NULL && pb != NULL)
    {
        if (pa->data == pb->data) {                             // 如果两个集合的这个元素相同，存入新集合中后指向下一个元素
            pc->link = new SetNode(pa->data);
            pa = pa->link; pb = pb->link;
        }
        else if (pa->data < pb->data) {                     // this集合元素值小
            pc->link = new SetNode(pa->data);
            pa = pa->link;                                            // 把this集合的这个元素存入，并且指向下一个元素
        }
        else {      // R集合的元素值小
            pc->link = new SetNode(pb->data);
            pb = pb->link;
        }
        pc = pc->link;   // 存了就指向下一个元素
    }

    if (pa != NULL) p = pa;                                     // pa集合没扫完
    else p = pb;                                                      // pb集合没扫完
    while (p != NULL) {
        pc->link = new SetNode(p->data);
        pc = pc->link;
        p = p->link;
    }

    pc->link = NULL;
    temp.last = pc;
    return temp;                                    // 链表收尾

}

LinkedSet& LinkedSet::operator*(LinkedSet& R)
{   // 计算R和this集合的相交
    SetNode* pb = R.first->link;  
    SetNode* pa = first->link;
    LinkedSet temp;
    SetNode* pc = temp.first;           // 存放结果的集合
    while (pa != NULL && pb!= NULL)
    {
        if (pa->data = pb->data)
        {                      // 两集合公有的元素
            pc->link = new SetNode(pa->data);
            pc = pc->link;
            pa = pa->link;
            pb = pb->link;
        }
        else if (pa->data < pb->data) pa = pa->link;            // 如果元素不相等，则不付给新的集合，根据data大小决定指向哪个集合
        else pb = pb->link;
    }
    pc->link = NULL;
    temp.last = pc;
    return temp;
}

LinkedSet& LinkedSet::operator-(LinkedSet& R)
{
    SetNode* pb = R.first->link;
    SetNode* pa = first->link;
    LinkedSet temp;
    SetNode* pc = temp.first;           // 指向结果集合
    while (pa!=NULL&&pb!=NULL)
    {
        if (pa->data == pb->data)        // 两集合均有的元素，直接跳过
        {
            pa = pa->link;
            pb = pb->link;
        }
        else if (pa->data < pb->data)
        {   // 第一个集合有，第二个集合没有
            pc->link = new SetNode(pa->data);
            pc = pc->link;
            pa = pa->link;
        }
        else pb = pb->link;
    }

    // 有个集合遍历完成
    while (pa != NULL) {
        // pb 还剩就不管，pa还剩就全存进去
        pc->link = new SetNode(pa->data);
        pc = pc->link;
        pa = pa->link;
    }
    pc->link = NULL;
    temp.last = pc;
    return temp;
}

bool LinkedSet::Contains(const int x)
{
    SetNode* temp = first->link;                
    while (temp != NULL && temp->data < x)                      // 搜索到大于x为止，因为是升序排序
        temp = temp->link;
    if (temp != NULL && temp->data == x) return true;
    else return false;
}

bool LinkedSet::operator==(LinkedSet& R)
{
    // 判断this集合和R集合是否相等
    
    SetNode* pb = R.first->link;                // R集合的链扫描指针
    SetNode* pa = first->link;                  // this集合的链扫描指针
    while (pa !=NULL && pb != NULL)
    {
        if (pa->data == pb->data)
        {
            pa = pa->link;
            pb = pb->link;
        }
        else return false;
    }
    if (pa != NULL || pb != NULL) return false;

    return true;
}

3 并查集与等价类

将n个不同的元素划分成一组不相交的集合.插入集合时需要查询该元素归属于哪个集合的运算.

3.1 概念

并查集中需要集合名类型和集合元素类型。很多情况可以使用整数作为集合名，如果有n个元素，可以用1~n内的整数来表示元素。
实现方法一般用树形结构。树的每一个结点代表集合的一个单元素。所有集合的全集和构成一个森林，并用树和森林的父指针表示。其下标代表元素名。
如

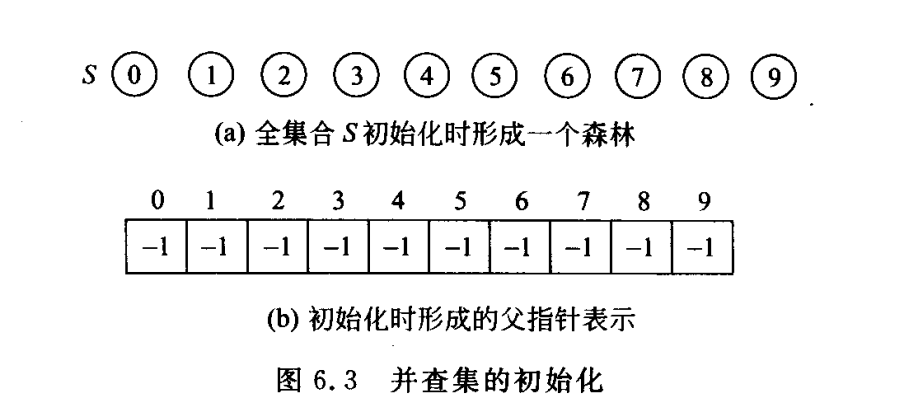
根节点必是复数，子结点存的是其父结点的下标。

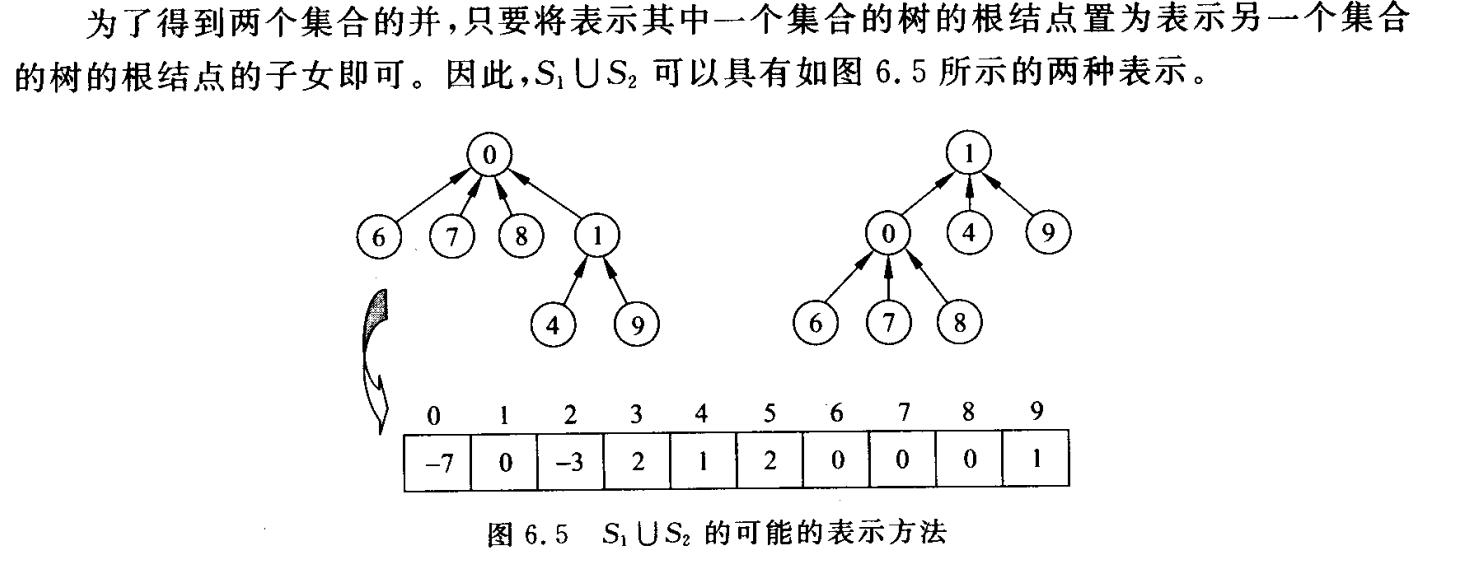
实现

#include <iostream>


const int DefaultSize = 10;

class UFSets {
public:
    UFSets(int sz = DefaultSize);
    ~UFSets() { delete[] parent; }
    UFSets& operator = (UFSets& R);         // 集合赋值
    void Union(int Root1, int Root2);           // 两个子集合并
    int Find(int x);                                        // 寻找根
    void WeightedUnion(int Root1, int Root2);       // 加权的合并算法
    int CollapsingFind(int i);
private:
    int* parent;        // 集合元素数组
    int size;               // 集合元素数目
};


int main()
{
    std::cout << "Hello World!\n";
}

UFSets::UFSets(int sz)
{
    size = sz;
    parent = new int[size];
    for (int i = 0; i < size; i++) parent[i] = -1;          // 初始化时每个结点自成一棵树
}

void UFSets::Union(int Root1, int Root2)
{
    parent[Root1] += parent[Root2];         
    parent[Root2] = Root1;                        // 这两部就是把root2变成root1的子结点
}

int UFSets::Find(int x)
{
    if (parent[x] < 0) return x;
    else return Find(parent[x]);
}

void UFSets::WeightedUnion(int Root1, int Root2)
{
    int r1 = Find(Root1);
    int r2 = Find(Root2);
    int temp;
    if (r1 != r2) {
        temp = parent[r1] + parent[r2];
        if (parent[r2] < parent[r1]) {
            parent[r1] = r2;
            parent[r2] = temp;
        }
        else { parent[r2] = r1; parent[r1] = temp; }

    }
}

int UFSets::CollapsingFind(int i)
{
    int j;
    for (j = i; parent[j] >= 0; j = parent[j]);             // 搜索根j
    while (i!=j)
    {
        int temp = parent[i];
        parent[i] = j;
        i = temp;
    }
    return i;
}

// 非递归方法
//int UFSets::Find(int x)
//{   
//    // 寻找包含元素x的树的根
//    while (parent[x] >=0) 
//    {
//        x = parent[x];
//    }
//    return x;
//}

4 字典

字典简单来说，定义为键值对**<名字-属性>**的集合。

4.1 字典的线性表描述

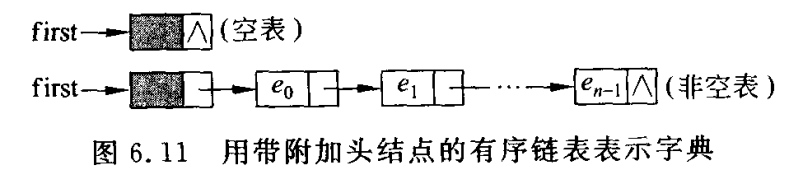
#include <iostream>
#include <assert.h>

using namespace std;

struct ChainNode
{
    int data;
    ChainNode* link;
    ChainNode() :link(NULL) {};
    ChainNode(int& e1, ChainNode* next = NULL) :data(e1), link(next) {};
};

class SortedChain {
public:
    SortedChain() {
        first = new ChainNode;
        assert(first != NULL);
    }
    ~SortedChain() { delete first; }
    ChainNode* Search(const int k1)const;               // 搜索
    void Insert(const int k1, int& e1);                         // 插入
    bool Remove(const int k1, int& e1);                      // 删除
    ChainNode* Begin() { return first->link; }
    ChainNode* Next(ChainNode* current)const {
        if (current != NULL) return current->link;
        else return NULL;
    }
private:
    ChainNode* first;
};

int main()
{
    std::cout << "Hello World!\n";
}

ChainNode* SortedChain::Search(const int k1) const
{
    ChainNode* p = first->link;
    while (p != NULL && p->data < k1) p = p->link;      
    if (p != NULL && p->data == k1) return p;
    else return NULL;
}

void SortedChain::Insert(const int k1, int& e1)
{
    ChainNode* p = first->link;         // 前面的指针
    ChainNode* pre = first;                 // 后面的指针 （用于插入在前面和后面指针之间
    ChainNode* newNode;
    while (p != NULL && p->data < k1) {
        pre = p;
        p = p->link;
    }
    if (p != NULL && p->data == k1) { p->data = e1; return; }       // 如果有键相同，换值
    newNode = new ChainNode(e1);
    if (newNode == NULL) {
        cout << "error when allocate memory" << endl;
        exit(1);
    }
    newNode->link = p;
    pre->link = newNode;
}

bool SortedChain::Remove(const int k1, int& e1)
{
    ChainNode* p = first->link;
    ChainNode* pre = first;
    while (p != NULL && p->data < k1) 
    {
        pre = p;
        p = p->link;
    }
    if (p != NULL && p->data == k1) 
    {
        pre->link = p->link;
        e1 = p->data;
        delete p;
        return true;
    }
    else return false;
}

5 跳表

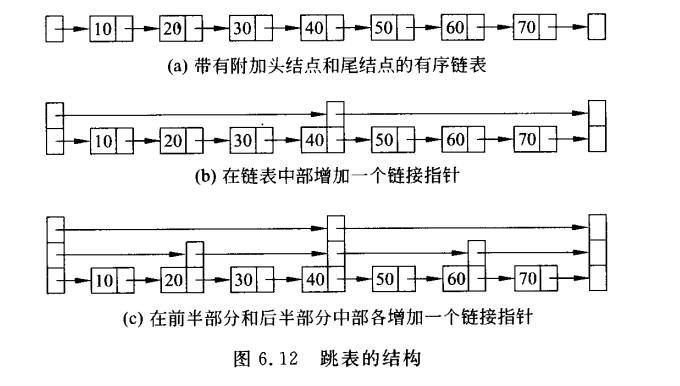
方便查找，在表的中间添加指针，在查找的时候在中间指针处开始，节省搜索时间。

6. 散列表

通过关键码计算得到键，随后获得到值的表。元素的存储位置与他的关键码之间建立一个确定的对应函数关系Hash()，使得每个关键码与结构的唯一存储位置相对应，相当于函数。

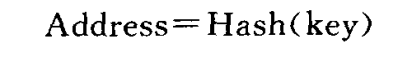
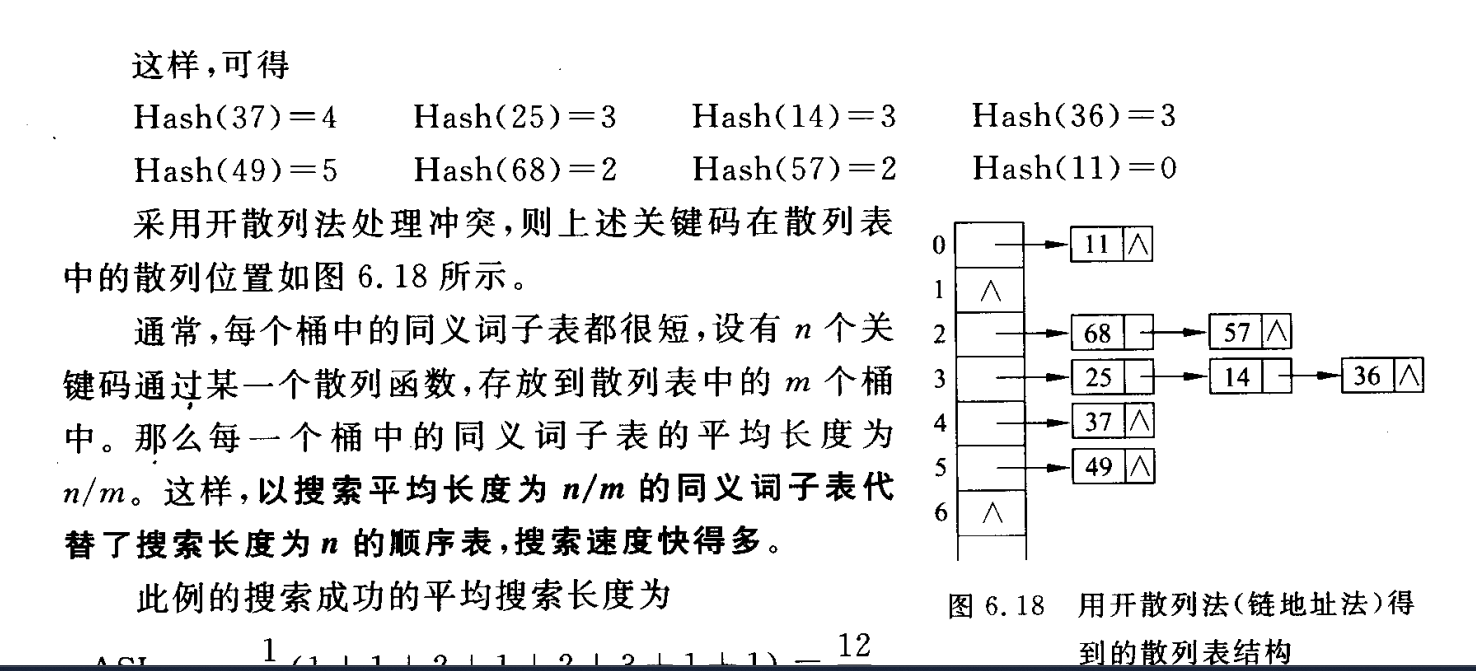
在计算散列函数时，不同的关键码对应相同的散列值，此时需要解决冲突。一般通过指定一个分布较均匀的散列函数，或者拟定解决冲突的方案。

6.1 散列函数

关于散列函数，书上举了几个例子

其实散列表中的散列函数不是很需要探讨的问题，解决冲突才是比较需要探讨的。

6.2 解决冲突的方法

6.2.1 线性探查法

简单来讲，如果有冲突，则找到下一个装数据的位置装这个数据。

#include <iostream>
using namespace std;

const int DefaultSize = 100;
enum KindOfStatus {
    Active,
    Empty,
    Deleted,
};

class HashTable {
public:
    HashTable(const int d, int sz = DefaultSize);
    ~HashTable() { delete[]ht; delete[]info; }
    HashTable& operator = (const HashTable& ht2);
    bool Search(const int k1, int& e1)const;    // 在散列表中搜索k1
    bool Insert(const int& e1);                         // 插入e1
    bool Remove(const int k1, int& e1);          // 散列表中删除e1
    void makeEmpty();
private:
    int divitor;        // 散列函数的除数（用来算散列值的）
    int CurrentSize;        // 当前存的数量
    int TableSize;          // 最大存的数量
    int* ht;            // 散列表存储数组
    KindOfStatus* info;     // 状态数组
    int FindPos(const int k1)const;
    int operator == (int& e1) { return *this == e1; }
    int operator !=(int& e1) { return *this != e1; }
};

HashTable::HashTable(const int d, int sz)
{
    divitor = d;
    TableSize = sz;
    CurrentSize = 0;
    ht = new int[TableSize];
    info = new KindOfStatus[TableSize];
    for (int i = 0; i < TableSize; i++)
        info[i] = Empty;
}

HashTable& HashTable::operator=(const HashTable& ht2)
{
    if (this != &ht2) { //   防止自我复制
        delete[] ht;
        delete[]info;
        TableSize = ht2.TableSize;
        ht = new int[TableSize];
        info = new KindOfStatus[TableSize];
        for (int i = 0; i < TableSize; i++) {
            ht[i] = ht2.ht[i];
            info[i] = ht2.info[i];
        }
        CurrentSize = ht2.CurrentSize;
    }
    return *this;
}

bool HashTable::Search(const int k1, int& e1) const
{
    int i = FindPos(k1);
    if (info[i] != Active || ht[i] != k1) return false;
    e1 = ht[i];
    return true;
}

bool HashTable::Insert(const int& e1)
{
    int k1 = e1;
    int i = FindPos(k1);
    if (info[i] != Active) {

        ht[i] = e1;
        info[i] = Active;
        CurrentSize++;
        return true;
    }
    if (info[i] == Active && ht[i] == e1) {
        cout << "already exist, can not insert!" << endl;
        return false;
    }
    cout << "full memory, can not insert!" << endl;
            return false;
}

bool HashTable::Remove(const int k1, int& e1)
{
    int i = FindPos(k1);
    if (info[i] == Active) {
        info[i] = Deleted;
        CurrentSize--;
        return true;
    }
    else return false;
}

int HashTable::FindPos(const int k1) const
{
    // 查找散列表中关键码与k1匹配的元素
    int i = k1 % divitor;
    int j = i;
    do {
        if (info[j] == Empty || info[j] == Active && ht[j] == k1) return j;
        j = (j + 1) % TableSize;
    } while (j != i);

    return j;
}

void HashTable::makeEmpty()
{
    for (int i = 0; i < TableSize; i++) info[i] = Empty;
    CurrentSize = 0;
}

int main()
{
    std::cout << "Hello World!\n";
}

6.2.2 二次探查法

有点难理解，看代码

int HashTable::FindPos(const int k1) const
{
    int i = k1 % divitor;
    int k = 0;                  // k是探查次数
    int odd = 0;            // odd是控制加减标志
    int j;
    int save = 0;
    while (info[i] == Active && ht[i] != k1) {
        if (odd == 0) {          // 上图中odd =0，即 (H0+i^2)%TableSize 的情形
            k++;
            save = i;
            i = (i + 2 * k - 1) % TableSize;            // 求下一个存储空间
            odd = 1;
        }
        else {
            i = (save - 2 * k + 1) % TableSize;       // 上图中odd =1，即 (H0-i^2)%TableSize 的情形
            odd = 0;
            if (i < 0)i = i + TableSize;                    // 求下一个存储空间
        }
    }

    return i;
}

bool HashTable::Insert(const int& e1)
{
    int k1 = e1;
    int i = FindPos(k1), j, k;      // 计算函数
    if (info[i] == Active) return false;        // 搜索成功，不插入
    ht[i] = e1;
    info[i] = Active;
    if (++CurrentSize < TableSize / 2) return true;         // 不超过表长的一半返回true
    int* OldHt = ht;
    KindOfStatus* oldInfo = info;
    int OldTableSize = TableSize;
    CurrentSize = 0;
    TableSize = NextPrime(2 * OldTableSize);        // 原表大小的两倍，取质数
    divitor = TableSize;
    ht = new int[TableSize];
    if (ht == NULL) {
        cout << "error when allocate memory!" << endl;
        return false;
    }
    info = new KindOfStatus[TableSize];
    if (info == NULL) {
        cout << "error when allocate memory!" << endl;
        return false;
    }
    for (j = 0; j < TableSize; j++) info[j] = Empty;
    for (i = 0; i < TableSize; i++)
        if (oldInfo[i] == Active) Insert(OldHt[i]);
    delete[] OldHt;
    delete[] oldInfo;
    return true;

}

还有个双散列表的方法，就不介绍了

6.2.3 开散列方法