【Datawhale 大模型基础】第一章：引言

第一章 引言

Large Language Model (LLM) has gradually attracted the attention of researchers in both the academic and industrial fields due to its outstanding performance in Natural Language Processing (NLP) and other domains.

Many beginners want to delve into the principles and related knowledge of LLMs. And thanks to datawhale, an open-source learning organization, I will follow the repo from the github and combine it with a general survey about LLMs to make some notes.

Before systematically studying LLMs, it is necessary to know what is Language Model (LM), a cornerstone of LLM.

In general, LM aims to model the generative likelihood of word sequences, so as to predict the probabilities of future (or missing) tokens.

For example, considering two sentences: “mouse the the cheese ate” and “the mouse ate the cheese”, for humans, we know that the second one is consistent with our syntax knowledge. Therefore, we naturally want to assign a higher value to the latter.

Mathematically, the definition of LM can be written as:

p ( x 1 , … , x L ) , { x 1 , . . . , x L } ∈ V p(x_1, \dots, x_L), \{x_{1},...,x_{L}\} \in \mathbb{V} p(x1?,…,xL?),{x1?,...,xL?}∈V

where $\mathbb{V}$ is the set of tokens while $x_i$ stands for the token of a target sentence.

The common way to express the joint distribution of a sequence is to use the chain rule of probability, which can be formulated as,

$$p(x_{1:L})=p(x_1)p(x_2\mid x_1)p(x_3\mid x_1,x_2)?p(x_L\mid x_{1:L?1})=\prod _{i=1}^{L}p(x_i\mid x_{1:i?1}).$$

where $p(x_1:x_L)$ is equal to $p(x_1,\dots ,x_L)$ aforementioned.

A vital notion, $p(x_L\mid x_{1:L?1})$, is the possibility of $x_L$ as the next token after the sequence $x_{1:L?1}$.

The research of LM has received extensive attention, which can be divided into four major development stages:

1. Statistical language models (SLM). SLMs are based on statistical learning methods whose basic idea is to build the word prediction model. As mentioned in the equation before, a canonical LM use $p(x_L\mid x_{1:L?1})$ to judge the next token, and this method is time-consuming when the sequence gets longer. Therefore, n-gram model was invented, the prediction about $x_i$ depends only on the last $n?1$ characters $x_{i?(n?1):i?1}$, not the entire history. For example, $p(cheese|the,mouse,ate,the)=p(cheese\mid ate,the)$.
2. Neural language models (NLM). NLMs represent the likelihood of word sequences using neural networks, such as multi-layer perceptron (MLP) and recurrent neural networks (RNNs).
3. Pre-trained language models (PLM). The pre-trained context-aware word representations have proven highly effective as general-purpose semantic features. This research has sparked numerous subsequent studies, establishing the “pre-training and fine-tuning” learning approach. In line with this approach, a multitude of studies on PLMs have emerged, introducing various architectures, like BERT.
4. Large language models (LLM). Researchers have observed that increasing the scale of PLMs (e.g., by scaling model size or data size) frequently results in enhanced model capacity for downstream tasks. So several studies have investigated the performance ceiling by training increasingly larger PLMs. And recently, there is a trend to study LLMs, regardless of the researchers from academic or industrial fields.

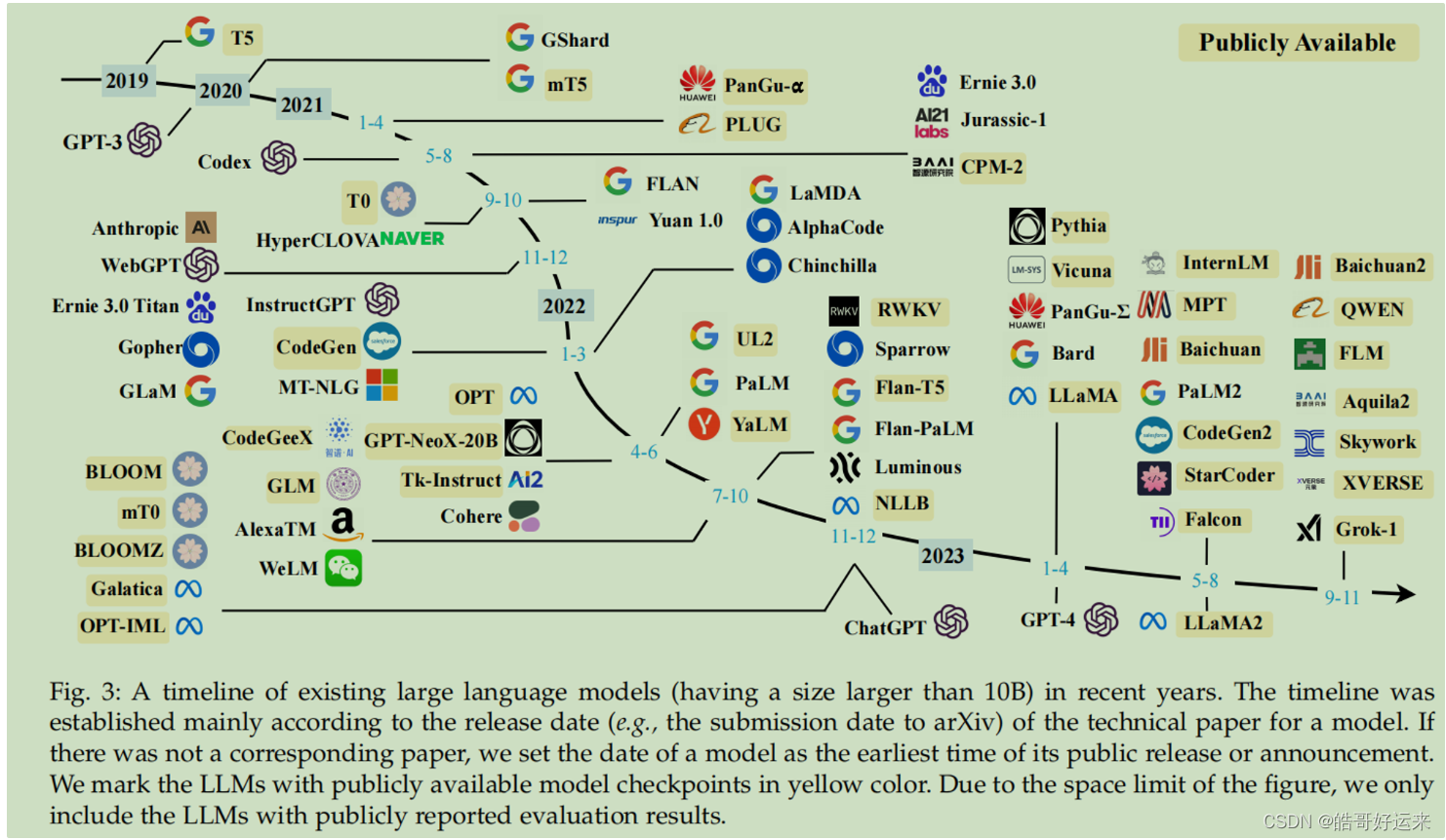
Figures are cited from the general survey.
For LLMs, they have competitive power in many domains, such as title generation, knowledge Q&A. At the same time, they also bring some potential risks, like bias and hallucination. Also, as a LLM can have 7B or more parameters, cost (both training cost and fine-tune cost) is a major barrier to widespread access. As a result, efficient tuning is becoming a research hotspot.

END