【数据结构】布隆过滤器原理详解及其代码实现
???《博主简介》
小伙伴们好,我是阿旭。专注于人工智能AI、python、计算机视觉相关分享研究。
?更多学习资源,可关注公-仲-hao:【阿旭算法与机器学习】,共同学习交流~
👍感谢小伙伴们点赞、关注!
《------往期经典推荐------》
一、AI应用软件开发实战专栏【链接】
二、机器学习实战专栏【链接】,已更新31期,欢迎关注,持续更新中~~
三、深度学习【Pytorch】专栏【链接】
四、【Stable Diffusion绘画系列】专栏【链接】
布隆过滤器(Bloom Filter)是一个占用空间很小、效率很高的随机数据结构,它由一个bit数组和一组Hash算法构成。可用于判断一个元素是否在一个集合中,查询效率很高(1-N,最优能逼近于1)。
在很多场景下,我们都需要一个能迅速判断一个元素是否在一个集合中。譬如:
网页爬虫对URL的去重,避免爬取相同的URL地址;
反垃圾邮件,从数十亿个垃圾邮件列表中判断某邮箱是否垃圾邮箱(同理,垃圾短信);
缓存击穿,将已存在的缓存放到布隆中,当黑客访问不存在的缓存时迅速返回避免缓存及DB挂掉。
可能有人会问,我们直接把这些数据都放到数据库或者redis之类的缓存中不就行了,查询时直接匹配不就OK了?
是的,当这个集合量比较小,你内存又够大时,是可以这样做,你可以直接弄个HashSet、HashMap就OK了。但是当这个量以数十亿计,内存装不下,数据库检索极慢时该怎么办。
以垃圾邮箱为例
方案比较
1.将所有垃圾邮箱地址存到数据库,匹配时遍历
2.用HashSet存储所有地址,匹配时接近O(1)的效率查出来
3.将地址用MD5算法或其他单向映射算法计算后存入HashSet,无论地址多大,保存的只有MD5后的固定位数
4.布隆过滤器,将所有地址经过多个Hash算法,映射到一个bit数组;怎么判断一个外来的元素是否已经在集合里呢?如果映射的元素的中包含0,则该元素一定不在集合里,如果该元素映射的都为1,那么该元素可能在数组里。
优缺点
方案1和2都是保存完整的地址,占用空间大。一个地址16字节,10亿即可达到上百G的内存。HashSet效率逼近O(1),数据库就不谈效率了,不在一个数量级。
方案3保存部分信息,占用空间小于存储完整信息,存在冲突的可能(非垃圾邮箱可能MD5后和某垃圾邮箱一样,概率低)
方案4将所有地址经过Hash后映射到?同一个bit数组,看清了,只有一个超大的bit数组,保存所有的映射,占用空间极小,冲突概率高。
大家知道,java中的HashMap有个扩容参数默认是0.75,也就是你想存75个数,至少需要一个100的数组,而且还会有不少的冲突。实际上,Hash的存储效率是0.5左右,存5个数需要10个的空间。算起来占用空间还是挺大的。
而布隆过滤器就不用为每个数都分配空间了,而是直接把所有的数通过算法映射到同一个数组,带来的问题就是冲突上升,只要概率在可以接受的范围,用时间换空间,在很多时候是好方案。布隆过滤器需要的空间仅为HashMap的1/8-1/4之间,而且它不会漏掉任何一个在黑名单的可疑对象,问题只是会误伤一些非黑名单对象。
原理
经过K个哈希算法将每个算法将元素映射到数组中的位置标1;
初始化状态是一个全为0的bit数组
![]()
?
为了表达存储N个元素的集合,使用K个独立的函数来进行哈希运算。x1,x2……xk为k个哈希算法。
如果集合元素有N1,N2……NN,N1经过x1运算后得到的结果映射的位置标1,经过x2运算后结果映射也标1,已经为1的1保持不变。经过k次散列后,对N1的散列完成。
依次对N2,NN等所有数据进行散列,最终得到一个部分为1,部分位为0的字节数组。当然了,这个字节数组会比较长,不然散列效果不好。

那么怎么判断一个外来的元素是否已经在集合里呢,譬如已经散列了10亿个垃圾邮箱,现在来了一个邮箱,怎么判断它是否在这10亿里面呢?
很简单,就拿这个新来的也依次经历x1,x2……xk个哈希算法即可。
在任何一个哈希算法譬如到x2时,得到的映射值有0,那就说明这个邮箱肯定不在这10亿内。
如果是一个黑名单对象,那么可以肯定的是所有映射都为1,肯定跑不了它。也就是说是坏人,一定会被抓。
那么误伤是为什么呢,就是指一些非黑名单对象的值经过k次哈希后,也全部为1,但它确实不是黑名单里的值,这种概率是存在的,但是是可控的。
什么情况下需要布隆过滤器?
先来看几个比较常见的例子
- 字处理软件中,需要检查一个英语单词是否拼写正确
- 在 FBI,一个嫌疑人的名字是否已经在嫌疑名单上
- 在网络爬虫里,一个网址是否被访问过
- yahoo, gmail等邮箱垃圾邮件过滤功能
这几个例子有一个共同的特点:?如何判断一个元素是否存在一个集合中?
常规思路
- 数组
- 链表
- 树、平衡二叉树、Trie
- Map (红黑树)
- 哈希表
虽然上面描述的这几种数据结构配合常见的排序、二分搜索可以快速高效的处理绝大部分判断元素是否存在集合中的需求。但是当集合里面的元素数量足够大,如果有500万条记录甚至1亿条记录呢?这个时候常规的数据结构的问题就凸显出来了。数组、链表、树等数据结构会存储元素的内容,一旦数据量过大,消耗的内存也会呈现线性增长,最终达到瓶颈。有的同学可能会问,哈希表不是效率很高吗?查询效率可以达到O(1)。但是哈希表需要消耗的内存依然很高。使用哈希表存储一亿 个垃圾 email 地址的消耗?哈希表的做法:首先,哈希函数将一个email地址映射成8字节信息指纹;考虑到哈希表存储效率通常小于50%(哈希冲突);因此消耗的内存:8 * 2 * 1亿 字节 = 1.6G 内存,普通计算机是无法提供如此大的内存。这个时候,布隆过滤器(Bloom Filter)就应运而生。在继续介绍布隆过滤器的原理时,先讲解下关于哈希函数的预备知识。
哈希函数
哈希函数的概念是:将任意大小的数据转换成特定大小的数据的函数,转换后的数据称为哈希值或哈希编码。下面是一幅示意图:

可以明显的看到,原始数据经过哈希函数的映射后称为了一个个的哈希编码,数据得到压缩。哈希函数是实现哈希表和布隆过滤器的基础。
布隆过滤器介绍
- 巴顿.布隆于一九七零年提出
- 一个很长的二进制向量 (位数组)
- 一系列随机函数 (哈希)
- 空间效率和查询效率高
- 有一定的误判率(哈希表是精确匹配)
布隆过滤器原理
布隆过滤器(Bloom Filter)的核心实现是一个超大的位数组和几个哈希函数。假设位数组的长度为m,哈希函数的个数为k
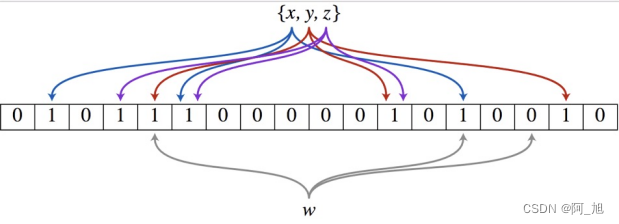
以上图为例,具体的操作流程:假设集合里面有3个元素{x, y, z},哈希函数的个数为3。首先将位数组进行初始化,将里面每个位都设置位0。对于集合里面的每一个元素,将元素依次通过3个哈希函数进行映射,每次映射都会产生一个哈希值,这个值对应位数组上面的一个点,然后将位数组对应的位置标记为1。查询W元素是否存在集合中的时候,同样的方法将W通过哈希映射到位数组上的3个点。如果3个点的其中有一个点不为1,则可以判断该元素一定不存在集合中。反之,如果3个点都为1,则该元素可能存在集合中。注意:此处不能判断该元素是否一定存在集合中,可能存在一定的误判率。可以从图中可以看到:假设某个元素通过映射对应下标为4,5,6这3个点。虽然这3个点都为1,但是很明显这3个点是不同元素经过哈希得到的位置,因此这种情况说明元素虽然不在集合中,也可能对应的都是1,这是误判率存在的原因。
布隆过滤器添加元素
- 将要添加的元素给k个哈希函数
- 得到对应于位数组上的k个位置
- 将这k个位置设为1
布隆过滤器查询元素
- 将要查询的元素给k个哈希函数
- 得到对应于位数组上的k个位置
- 如果k个位置有一个为0,则肯定不在集合中
- 如果k个位置全部为1,则可能在集合中
布隆过滤器实现
| import?mmh3 from?bitarray import?bitarray # zhihu_crawler.bloom_filter # Implement a simple bloom filter with murmurhash algorithm. # Bloom filter is used to check wether an element exists in a collection, and it has a good performance in big data situation. # It may has positive rate depend on hash functions and elements count. BIT_SIZE =?5000000 class?BloomFilter: ???? ????def?__init__(self): ????????# Initialize bloom filter, set size and all bits to 0 ????????bit_array =?bitarray(BIT_SIZE) ????????bit_array.setall(0) ????????self.bit_array =?bit_array ???????? ????def?add(self,?url): ????????# Add a url, and set points in bitarray to 1 (Points count is equal to hash funcs count.) ????????# Here use 7 hash functions. ????????point_list =?self.get_postions(url) ????????for?b in?point_list: ????????????self.bit_array[b]?=?1 ????def?contains(self,?url): ????????# Check if a url is in a collection ????????point_list =?self.get_postions(url) ????????result =?True ????????for?b in?point_list: ????????????result =?result and?self.bit_array[b] ???? ????????return?result ????def?get_postions(self,?url): ????????# Get points positions in bit vector. ????????point1 =?mmh3.hash(url,?41)?%?BIT_SIZE ????????point2 =?mmh3.hash(url,?42)?%?BIT_SIZE ????????point3 =?mmh3.hash(url,?43)?%?BIT_SIZE ????????point4 =?mmh3.hash(url,?44)?%?BIT_SIZE ????????point5 =?mmh3.hash(url,?45)?%?BIT_SIZE ????????point6 =?mmh3.hash(url,?46)?%?BIT_SIZE ????????point7 =?mmh3.hash(url,?47)?%?BIT_SIZE ????????return?[point1,?point2,?point3,?point4,?point5,?point6,?point7] |
关于本篇文章大家有任何建议或意见,欢迎在评论区留言交流!
觉得不错的小伙伴,感谢点赞、关注加收藏哦!
欢迎关注下方GZH:阿旭算法与机器学习,共同学习交流~
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!