[足式机器人]Part2 Dr. CAN学习笔记-自动控制原理Ch1-7Lead Compensator超前补偿器（调节根轨迹）

2024-01-03 17:38:15

本文仅供学习使用
本文参考：
B站：DR_CAN

Dr. CAN学习笔记-自动控制原理Ch1-7Lead Compensator超前补偿器（调节根轨迹）

在这里插入图片描述

1. Plot Rootlocus 绘制根轨迹

G ( s ) = 1 s ( s + 2 ) G\left( s \right) =\frac{1}{s\left( s+2 \right)} G(s)=s(s+2)1?
在这里插入图片描述

2. System Performance 系统表现

输入Input —— δ ( t ) \delta \left( t \right) δ(t) 单位冲激

  • K K K 较小时， p 1 , p 2 p_1,p_2 p1?,p2? ： x ( t ) = c 1 e p 1 t + c 2 e p 2 t , p 1 < 0 , p 2 < 0 x\left( t \right) =c_1e^{p_1t}+c_2e^{p_2t},p_1<0,p_2<0 x(t)=c1?ep1?t+c2?ep2?t,p1?<0,p2?<0
    在这里插入图片描述
  • K K K 较大时，根在复平面： p 1 , p 2 p_1,p_2 p1?,p2? ： x ( t ) = c e ? t sin ? ω n t x\left( t \right) =ce^{-t}\sin \omega _{\mathrm{n}}t x(t)=ce?tsinωn?t - 无论如何改变 K K K值，都无法改变收敛速度
    -在这里插入图片描述

3. 改善/加快收敛速度

——改变根轨迹，希望根在 ? 2 + 2 3 -2+2\sqrt{3} ?2+23 ?
G ( s ) = 1 s ( s + 2 ) G\left( s \right) =\frac{1}{s\left( s+2 \right)} G(s)=s(s+2)1?
在根轨迹上的点满足： ∠ K G ( s ) = ? π \angle KG\left( s \right) =-\pi ∠KG(s)=?π （零点到根的夹角和 - 极点到根的夹角和）
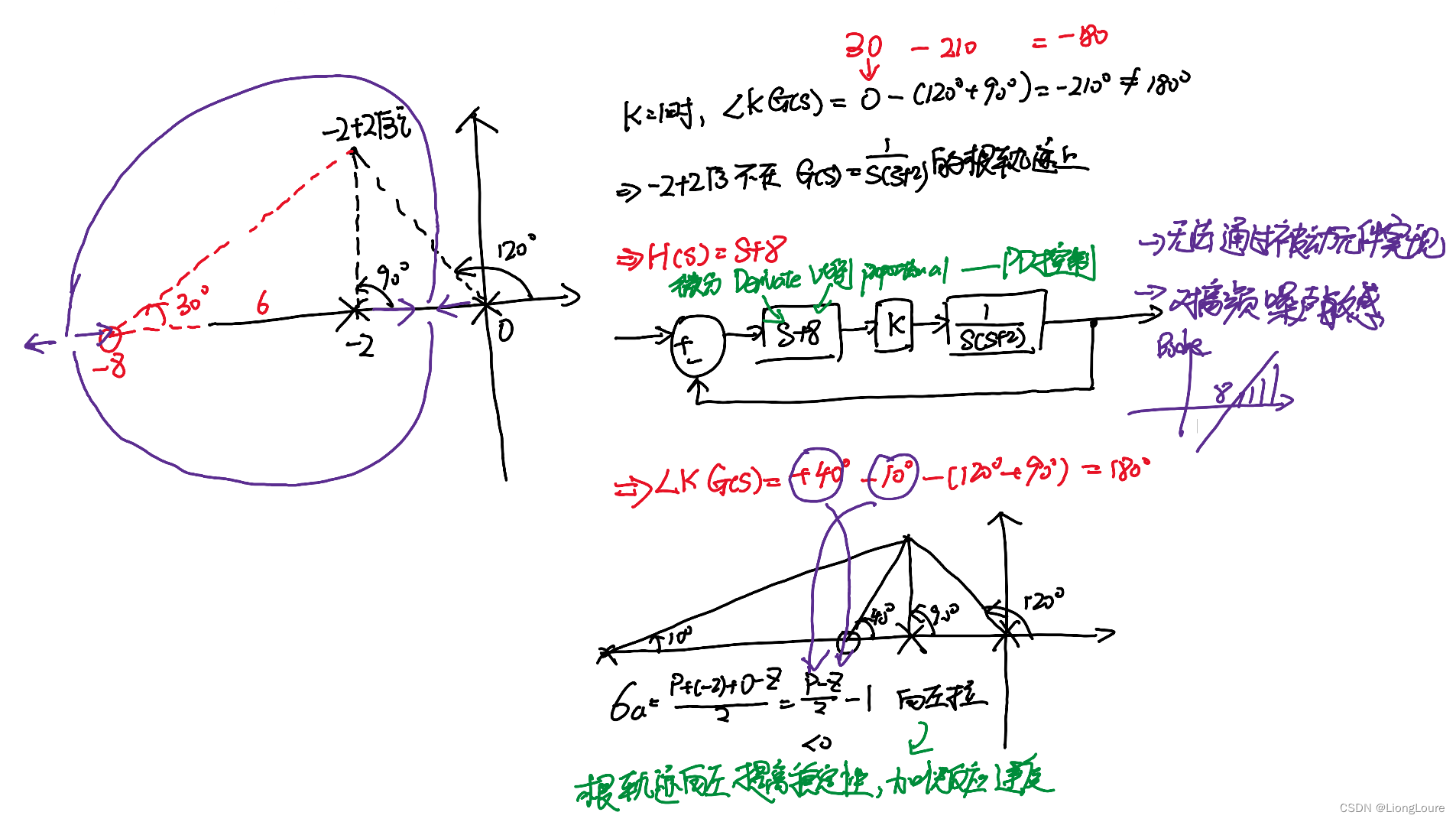
在这里插入图片描述

4. 超前补偿器 Lead Comperastor

H ( s ) = s ? z s ? p , ∥ z ∥ < ∥ p ∥ H\left( s \right) =\frac{s-z}{s-p},\left\| z \right\| <\left\| p \right\| H(s)=s?ps?z?,∥z∥<∥p∥
在这里插入图片描述

文章来源:https://blog.csdn.net/LiongLoure/article/details/135307831
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。