LeetCode:1402. 做菜顺序、2316. 统计无向图中无法互相到达点对数
1. 1402 做菜顺序
题目详细为:
一个厨师收集了他 n 道菜的满意程度 satisfaction ,这个厨师做出每道菜的时间都是 1 单位时间。
一道菜的 「 like-time 系数 」定义为烹饪这道菜结束的时间(包含之前每道菜所花费的时间)乘以这道菜的满意程度,也就是 time[i]*satisfaction[i] 。
返回厨师在准备了一定数量的菜肴后可以获得的最大 like-time 系数 总和。
你可以按 任意 顺序安排做菜的顺序,你也可以选择放弃做某些菜来获得更大的总和。
示例为:
示例 1:
输入:satisfaction = [-1,-8,0,5,-9]
输出:14
解释:去掉第二道和最后一道菜,最大的 like-time 系数和为 (-11 + 02 + 53 = 14) 。每道菜都需要花费 1 单位时间完成。
示例 2:
输入:satisfaction = [4,3,2]
输出:20
解释:可以按照任意顺序做菜 (21 + 32 + 43 = 20)
示例 3:
输入:satisfaction = [-1,-4,-5]
输出:0
解释:大家都不喜欢这些菜,所以不做任何菜就可以获得最大的 like-time 系数。
提示:
n == satisfaction.length
1 <= n <= 500
-1000 <= satisfaction[i] <= 1000
难度:【困难】
算法思路:
由于n的取值并没有很大,所以使用暴力解法解决这题完全没有问题,但是个人觉得可以这样来实现。
可以分为三类情况,(1)satisfaction这个数组(列表)中的最大数小于零,这样得到最终结果(按照上述公式)肯定小于0,那么直接返回0即可;(2)satisfaction这个数组(列表)中的最小数大于零,对这个数组进行升序排序,然后利用上述公式计算返回即可;(3)satisfaction这个数组(列表)中同时存在小于0和大于0的数,首先对这个数组进行升序排序,然后用一个变量根据上述公式计算对应结果num2,用变量num存储数组的和,之后再遍历这个数组,变量ans(初始值为0)返回最终结果,执行下述操作即可,ans = max(ans,num2),num2 -= num,num -= satisfaction[i],示意图如下:
satisfaction数组
排序前 [-1,-8,0,5,-9]
排序后 [-9,-8,-1,0,5]
num的值为:-13
num2的值为:-9 * 1 + -8 * 2 + -1 * 3 + 0 * 4 + 5 * 5 = -3
ans = 0
遍历次数 ans num num2
1 0 -13 -3
2 0 -4 10
3 10 4 14
4 14 5 10
5 14 5 5
参考代码如下:
class Solution(object):
def maxSatisfaction(self, satisfaction):
"""
:type satisfaction: List[int]
:rtype: int
"""
satisfaction.sort()
if satisfaction[-1] < 0:
return 0
ans = 0
n = len(satisfaction)
if satisfaction[0] > 0:
start = 1
for e in satisfaction:
ans += start * e
start += 1
else:
num = sum(satisfaction)
num2 = 0
for i in range(n):
num2 += satisfaction[i] * (i+1)
for i in range(n):
ans = max(ans,num2)
num2 -= num
num -= satisfaction[i]
return ans
a = Solution()
print(a.maxSatisfaction(satisfaction = [-1,-8,0,5,-9]))
运行结果:
虽然算法效率总体还不怎么的,但是比暴力肯定要好一些。
2. 2316. 统计无向图中无法互相到达点对数
题目详细为:
给你一个整数 n ,表示一张 无向图 中有 n 个节点,编号为 0 到 n - 1 。同时给你一个二维整数数组 edges ,其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条 无向 边。
请你返回 无法互相到达 的不同 点对数目 。
示例为:
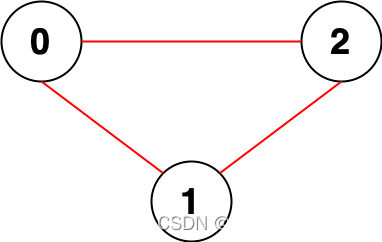
输入:n = 3, edges = [[0,1],[0,2],[1,2]]
输出:0
解释:所有点都能互相到达,意味着没有点对无法互相到达,所以我们返回 0 。
2.
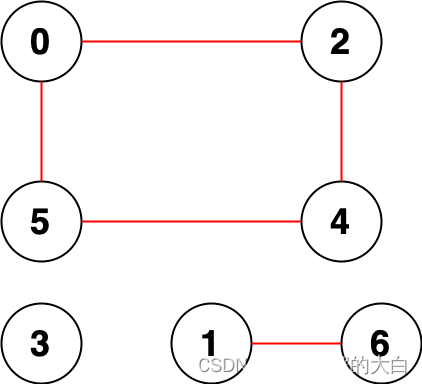
输入:n = 7, edges = [[0,2],[0,5],[2,4],[1,6],[5,4]]
输出:14
解释:总共有 14 个点对互相无法到达:
[[0,1],[0,3],[0,6],[1,2],[1,3],[1,4],[1,5],[2,3],[2,6],[3,4],[3,5],[3,6],[4,6],[5,6]]
所以我们返回 14 。
提示:
提示:
1 <= n <= 105
0 <= edges.length <= 2 * 105
edges[i].length == 2
0 <= ai, bi < n
ai != bi
不会有重复边。
算法思路:
从0号节点依次遍历到n-1号节点,如果遍历到某节点时,在map中已经存在了,那么不需要再进行接下来的操作,否则,在map中记录当前节点,然后依次遍历与该节点连通的节点,继续上述操作,直到遍历完某节点所有连通的节点,此时map中存储的节点个数减去pre(初始为0),即可得到一组不为0数,用一个数组arr存储,直到所有节点全部遍历完,然后计算arr中的数即可得到最终结果。但是有问题遍历arr需要两层,应该提交不了,为此直接在遍历节点的同时计算最终结果(但是最终还是差几个用例没有通过,最后参考官方代码改进才通过)。
参考代码为:
class Solution(object):
def countPairs(self, n, edges):
"""
:type n: int
:type edges: List[List[int]]
:rtype: int
"""
map = {}
for e in range(n):
map[e] = []
for key,value in edges:
map[key].append(value)
map[value].append(key)
map2 = {}
def dfs(cur_node):
map2[cur_node] = 1
arr = map[cur_node]
count = 1
for e in arr:
if not map2.get(e,None):
count += dfs(e)
return count
ans = 0
pre = 0
for i in range(n):
if not map2.get(i,None):
count = dfs(i)
ans += pre * count
pre += count
return ans
运行结果:

本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!