中后缀表达式
一、利用后缀表达式进行计算
1)解题思路
- 如果当前字符串是操作数,就将该操作数入栈;
- 如果当前字符串是操作符,就取栈顶的两个操作数进行运算(注意:第一个出栈的数为计算时的右操作数;第二个出栈的数为计算是的左操作数),并将运算结果重新入栈;
- 重复上面两个步骤,直到字符串遍历完:最后栈里面的值就是计算结果。
2)代码
int evalRPN(vector<string>& tokens)
{
stack<int> st;
// 遍历字符
for(auto& e : tokens)
{
// 如果遇到的是运算符,取出栈中的两个元素运算,并将运算结果入栈
if(e == "+" || e == "-" || e == "*" || e == "/")
{
int num2 = st.top();
st.pop();
int num1 = st.top();
st.pop();
if(e == "+")
st.push(num1+num2);
if(e == "-")
st.push(num1-num2);
if(e == "*")
st.push(num1*num2);
if(e == "/")
st.push(num1/num2);
}
// 如果是操作数,如入栈
else
{
st.push(stoi(e));
}
}
return st.top();
}
};3)注意点
如果当前字符串为操作数时,需要先使用 stoi() 函数将字符串转化为数字后,将其入栈。

题目链接:
二、中缀表达式转后缀表达式
1)解题思路
- 如果当前字符为操作数,直接输出;
- 如果当前字符为操作符,判断当前栈是否为空:
- 如果栈为空,将该操作符入栈;
- 如果栈不为空,将该操作符与栈顶元素比较优先级:
- 如果当前操作符优先级高,入栈;
- 如果当前操作符优先级相等或较低,输出栈顶元素。
还需要考虑,括号带来的优先级问题:不能仅仅根据运算符本身的优先级进行比较。
这里有好几种处理方法,在这里我介绍一种:
- 遇到 ( 时,将它入栈,并且认为它的优先级是最低的,这样才能保证括号内部的操作符才能入栈;
- 同时遇到 ) 时,我们还是认为它的优先级是最低的,这样才能保证括号内部的操作符能够出栈进行计算,并且出栈 - 后,并且遇到( 后,将其出栈。
- 最后如果栈空也不进行入栈操作,并进行下一个操作的判断。
括号的特殊处理,总结一下:
- ()的优先级最低;
- ( 不进行优先级的比较,直接入栈;
- ) 进行比较,输出栈顶元素,直到遇到( 。
下面举个例子,模拟一个这个过程:
当将中缀表达式1+2*(4-5*2)+6/7转化为后缀表达式时,可以按照以下步骤进行:
-
创建一个空栈和一个空列表(用于存放后缀表达式)。
-
从左到右遍历中缀表达式中的每个元素,按照以下规则处理:
-
遇到数字时,直接加入到后缀表达式列表中。
-
遇到运算符时,分两种情况:
- 如果栈为空或者栈顶元素为左括号,将当前运算符压入栈中。
- 否则,如果当前运算符的优先级小于等于栈顶运算符的优先级,则将栈顶运算符弹出并加入到后缀表达式列表中,直到栈顶运算符的优先级小于当前运算符的优先级或者栈为空,然后将当前运算符压入栈中。
-
遇到左括号时,将其压入栈中。
-
遇到右括号时,依次弹出栈顶元素并加入到后缀表达式列表中,直到遇到左括号为止。注意:左右括号不应该加入到后缀表达式列表中。
-
-
如果中缀表达式已经遍历完毕,则将栈中剩余的运算符依次弹出并加入到后缀表达式列表中。
-
后缀表达式列表即为转换得到的后缀表达式。
以下是将中缀表达式1+2*(4-5*2)+6/7转化为后缀表达式的详细过程:
-
初始化栈和后缀表达式列表为空。
-
从左到右遍历中缀表达式:
- 遇到字符'1',加入后缀表达式列表:
['1'] - 遇到字符'+',将其压入栈中:栈:
['+'] - 遇到字符'2',加入后缀表达式列表:
['1', '2'] - 遇到字符'*',将其压入栈中:栈:
['+', '*'] - 遇到字符'(',将其压入栈中:栈:
['+', '*', '('] - 遇到字符'4',加入后缀表达式列表:
['1', '2', '4'] - 遇到字符'-',将其压入栈中:栈:
['+', '*', '(', '-'] - 遇到字符'5',加入后缀表达式列表:
['1', '2', '4', '5'] - 遇到字符'*',将其压入栈中:栈:
['+', '*', '(', '-', '*'] - 遇到字符'2',加入后缀表达式列表:
['1', '2', '4', '5', '2'] - 遇到字符')',弹出栈顶元素并加入后缀表达式列表,直到遇到左括号为止:
['1', '2', '4', '5', '2', '*', '-'] - 弹出左括号'('。
- 遇到字符'+',将其压入栈中:栈:
['+', '+'] - 遇到字符'6',加入后缀表达式列表:
['1', '2', '4', '5', '2', '*', '-', '6'] - 遇到字符'/',将其压入栈中:栈:
['+', '+', '/'] - 遇到字符'7',加入后缀表达式列表:
['1', '2', '4', '5', '2', '*', '-', '6', '7']
- 遇到字符'1',加入后缀表达式列表:
-
中缀表达式已经遍历完毕,将栈中剩余的运算符依次弹出并加入到后缀表达式列表中:
['1', '2', '4', '5', '2', '*', '-', '6', '7', '/', '+', '+'] -
后缀表达式为
1 2 4 5 2 * - * + 6 7 / +。
这就是将中缀表达式1+2*(4-5*2)+6/7转化为后缀表达式的详细过程。
2)代码
#include <iostream>
#include <stack>
#include <string>
#include <vector>
bool isOperator(char ch) {
return (ch == '+' || ch == '-' || ch == '*' || ch == '/');
}
int getPriority(char op) {
if (op == '+' || op == '-')
return 1;
else if (op == '*' || op == '/')
return 2;
return 0;
}
std::vector<std::string> infixToPostfix(const std::string& infix) {
std::vector<std::string> postfix;
std::stack<char> opStack;
for (unsigned i = 0; i < infix.length(); ++i) {
char ch = infix[i];
if (ch == ' ') {
continue;
}
else if (isdigit(ch)) {
std::string num;
while (i < infix.length() && (isdigit(infix[i]) || infix[i] == '.')) {
num += infix[i++];
}
--i;
postfix.push_back(num);
}
else if (isOperator(ch)) {
while (!opStack.empty() && opStack.top() != '(' &&
getPriority(opStack.top()) >= getPriority(ch)) {
postfix.push_back(std::string(1, opStack.top()));
opStack.pop();
}
opStack.push(ch);
}
else if (ch == '(') {
opStack.push(ch);
}
else if (ch == ')') {
while (!opStack.empty() && opStack.top() != '(') {
postfix.push_back(std::string(1, opStack.top()));
opStack.pop();
}
opStack.pop(); // Discard '('
}
}
while (!opStack.empty()) {
postfix.push_back(std::string(1, opStack.top()));
opStack.pop();
}
return postfix;
}
int main() {
std::string infixExpression = "1+2*(4-5*2)+6/7";
std::vector<std::string> postfixExpression;
postfixExpression = infixToPostfix(infixExpression);
for (const auto& token : postfixExpression) {
std::cout << token << " ";
}
std::cout << std::endl;
return 0;
}

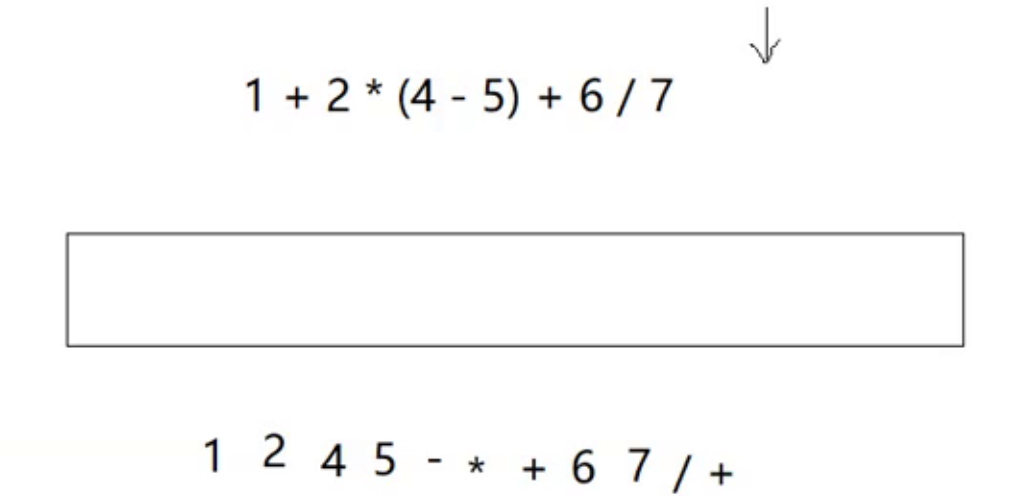
遇到 ( 时,将它入栈,并且认为它的优先级是最低的,这样才能保证括号内部的操作符才能入栈;
同时遇到 ) 时,我们还是认为它的优先级是最低的,这样才能保证括号内部的操作符能够出栈进行计算,并且出栈 - 后,并且遇到( 后,将其出栈,最后如果栈空也不进行入栈操作,并进行下一个操作的判断。
同时也可以使用增加一个flag标签的方法:
我们可以将这个flag初始化为0,只有遇到( 时,将flag = 1,通过flag的值判断下一个操作符的优先级,当flag = 1时,无论下一个操作符是什么,我们都认为它的优先级是高于此时栈顶操作符的,并进行入栈操作。当遇到)时,将flag置为0;
也可以使用递归,将()内部的表达式用一个新的栈进行计算,并将结果返回。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!