机器学习---Boosting

1. Boosting算法

Boosting思想源于三个臭皮匠，胜过诸葛亮。找到许多粗略的经验法则比找到一个单一的、高度预

测的规则要容易得多，也更有效。

预测明天是晴是雨？传统观念：依赖于专家系统（A perfect Expert)

以“人无完人”为基础，结合普通reporter，获得完美专家。

弱学习机（weak learner):? 对一定分布的训练样本给出假设（仅仅强于随机猜测），根据有云猜测

可能会下雨。强学习机（strong learner): 根据得到的弱学习机和相应的权重给出假设（最大程度上

符合实际情况：almost perfect expert)，根据CNN、ABC、CBS以往的预测表现及实际天气情况作

出综合准确的天气预测。

?

?

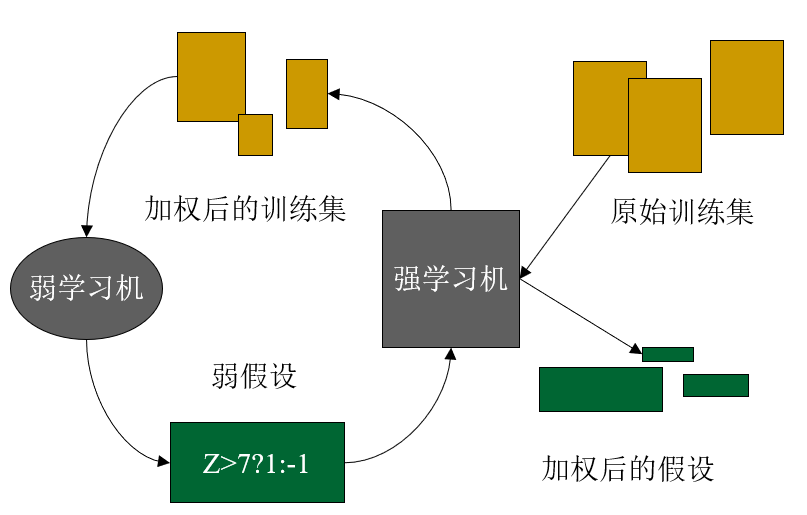
Boosting算法流程：

①原始训练集输入，带有原始分布

②给出训练集中各样本的权重

③将改变分布后的训练集输入已知的弱学习机，弱学习机对每个样本给出假设

④对此次的弱学习机给出权重

⑤转到②, 直到循环到达一定次数或者某度量标准符合要求

⑥将弱学习机按其相应的权重加权组合形成强学习机

样本的权重：没有先验知识的情况下，初始的分布应为等概分布，也就是训练集如果有N个样本，

每个样本的分布概率为1/N，每次循环一后提高错误样本的分布概率，分错样本在训练集中所占权

重增大， 使得下一次循环的弱学习机能够集中力量对这些错误样本进行判断。

弱学习机的权重：准确率越高的弱学习机权重越高。

循环控制：损失函数达到最小，在强学习机的组合中增加一个加权的弱学习机，使准确率提高，损

失函数值减小。

2. 算法思想

训练集

Dt为第t次循环时的训练样本分布（每个样本在训练集中所占的概率， Dt总和应该为1）。

ht:X∈{-1,+1} 为第t次循环时的Weak learner，对每个样本给出相应的假设，应该满足强于随机猜

测：

wt为ht的权重，为t次循环得到的Strong learner。

思想：提高分错样本的权重

反映了strong learner对样本的假设是否正确。

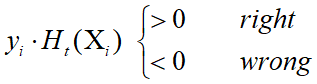? ? ? 采用什么样的函数形式？

思想：错误率越低，该学习机的权重应该越大

为学习机的错误概率，采用什么样的函数形式？

和指数函数遥相呼应：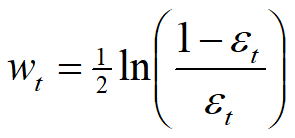

算法伪代码：

3. 理论分析?

如何求弱学习机的权重？

最基本的损失函数表达形式：

为了便于计算，采用以下的目标函数：

Boosting的循环过程就是沿着损失函数的负梯度方向进行最优化的过程。通过调整样本分布Dt和选

择弱学习机权重wt来达到这个目的。每循环一次，增加一项，使损失函数以最快速度下降。

给定当前分布和选定的弱学习机，如何求下一次的分布？?

Boosting的设计思想：

改变分布，提高错误样本概率，使下一次的弱学习机能够集中精力针对那些困难样本。

调整分布后的训练集对当前学习机具有最大的随机性，正确率50%（恰好为随机猜测）。

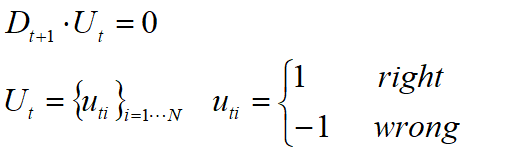
相对熵原理（最小鉴别信息原理）：

已知随机变量X（样本集）的先验分布（Dt），并且已知所求未知分布Dt+1满足条件

，那么所求得的未知分布估计值具有如下形式：

?。

物理意义：在只掌握部分信息的情况下要对分布作出判断时，应该选取符合约束条件但熵值取得最

大概率分布。从先验分布到未知分布的计算应该取满足已知条件，不确定度（熵）变化最小的解。

人脸识别方面的应用：

?