【形式语言与自动机/编译原理】CFG-->Greibach-->NPDA(3)
2024-01-01 10:56:33
本文将详细讲解《形式语言与自动机》(研究生课程)或《编译原理》(本科生课程)中的上下文无关文法(CFG)转换成Greibach范式,再转成下推自动机(NPDA)识别语言是否可以被接受的问题。此外,本文还给出了python代码的具体实现。
由于内容比较多,所以为了讲清楚,分成了3篇博客,第一篇主要讲 解从上下文无关文法到Greibach范式的具体步骤和流程,并给出了相应的算法及具体的例子;第二篇主要讲解从Greibach范式到下推自动机NPDA,同样给出了相应的算法及具体的例子;第三篇(即本篇)主要是对前两篇中给出的算法用python语言进行实现,并测试之前的例子。
它们的地址如下:
第一篇:
第二篇:
第三篇:
前面两篇博客已经给出了各个步骤的算法,本篇就直接上python代码了~
1 消除直接左递归
代码:
'''
4(1)、消除左递归(包括直接左递归)
(1)判断是否存在左递归 (2)消除左递归
'''
import random
#输出文法,格式规范化
def print_grammars(grammars:list):
for p in grammars:
print(p)
return
grammars=['S->aAD','A->bBb','B->Bd|$','D->cD|c','E->ab']
# grammars=['S->aAD','A->bBb','B->$|Bd|b','D->cD|c','E->ab']
# grammars=['S->c|bc|Sabc|Sa|abc', 'Q->Rb|b', 'R->Sa|a']#消除间接左递归测试例子1
# grammars=['A->d|aAc|Abc', 'B->aA|Ab']#消除间接左递归测试例子2
print('上下文无关文法:')
print_grammars(grammars)
print('-----------------------------------------------------------------------')
#判断是否存在直接左递归
def is_direct_zdg(grammars):
flag=False
direct_zdg_grammars=[]
for p in grammars:#遍历文法grammars中的每条规则,如果右部结果列表中某个结果的首字母=左部,那么这条规则就包含直接左递归,将该规则放到direct_zdg_grammars中
right=p[p.find('>')+1:].split('|')
left=p[:p.find('-')]
for res in right:
if res != '$' and res[0]==left:
direct_zdg_grammars.append(p)
flag=True
# print(direct_zdg_grammars)
if flag==True:
return flag,direct_zdg_grammars
else:
return flag
flag,direct_zdg_grammars=is_direct_zdg(grammars)
print('是否存在直接左递归:',flag)
print('包含直接左递归的规则集合:',direct_zdg_grammars)
#统计规则中的所有出现过的非终结符
def count_V(grammars):
used_V=''
for p in grammars:
for char in p:
if char in 'ABCDEFGHIJKLMNOPQRSTUVWXYZ' and char not in used_V:
used_V+=char
return used_V
used_V=count_V(grammars)
# print('文法grammars中出现过的所有非终结符:',used_V)
available_V=''
for char in 'ABCDEFGHIJKLMNOPQRSTUVWXYZ':
if char not in used_V:
available_V+=char
# print('没有出现在文法grammars中的所有可用非终结符:',available_V)
#消除直接左递归
def delete_direct_zdg(grammars,direct_zdg_grammars):
#找到不包含直接左递归的规则集合
rest_grammars=[]
for p in grammars:
if p not in direct_zdg_grammars and p not in rest_grammars:
rest_grammars.append(p)
# print('不包含直接左递归的规则集合:',rest_grammars)
for p in direct_zdg_grammars:
new_V=random.choice(available_V)#从没有出现过的可用非终结符中随机挑选一个非终结符作为新的V
right=p[p.find('>')+1:].split('|')
left=p[:p.find('-')]
#找到结果列表right中首字符不是left的结果
res_first_not_left=[res for res in right if res[0]!=left]
if '$' in res_first_not_left:
res_first_not_left[res_first_not_left.index('$')]=''
# print('规则右部结果中首字母不是左部的结果有:',res_first_not_left)
#找到结果列表中第一个字母是left的结果,除第一个字母外的剩余部分rest_sec
rest_sec=[]
for res in right:
if res[0]==left:
rest_sec.append(res[1:])
# print('结果除第一个字母外的剩余部分:',rest_sec)
new_p_ls = []
new_p1=left+'->'+'|'.join([char+new_V for char in res_first_not_left])
# print('消除直接左递归产生的第一个式子:',new_p1)
new_p2=new_V+'->'+'|'.join([char+new_V for char in rest_sec]+['$'])
# print('消除直接左递归产生的第二个式子:',new_p2)
new_p_ls.append(new_p1)
new_p_ls.append(new_p2)
#将消除直接左递归产生的两个式子加入到grammars中,更新gramms
grammars=rest_grammars+new_p_ls
return grammars
if flag==True:
print('消除直接左递归后的结果:')
print_grammars(delete_direct_zdg(grammars,direct_zdg_grammars))
print('-----------------------------------------------------------------------')
测试例子结果截图:

2 消除间接左递归
代码:
'''
4(2)、间接左递归
(1)判断是否存在间接左递归:把一个式子迭代到不能再迭代,这是判断是否存在直接左递归,若存在则说明存在间接左递归,否则不存在 (2)消除间接左递归:转换成直接左递归进行消除
'''
#输出文法,格式规范化
def print_grammars(grammars:list):
for p in grammars:
print(p)
return
# grammars=['A->Bc|d','B->aA|Ab']#存在间接左递归
# grammars=['S->Qc|c','Q->Rb|b','R->Sa|a']#存在间接左递归
grammars=['S->aAD','A->bBb','B->Bd|$','D->cD|c','E->ab']#不存在间接左递归
print("上下文无关文法:")
print_grammars(grammars)
print('-----------------------------------------------------------------------')
#将grammars由列表形式转换为字典形式,其中key为产生式的左边,value为产生式的右边的结果列表
grammars_dict=dict()
for p in grammars:
left = p[:p.find('-')]
right = p[p.find('>') + 1:].split('|')
grammars_dict[left]=right
print(grammars_dict)
#判断是否存在间接左递归:把一个式子迭代到底,如果存在间接左递归,那就直接将间接左递归转换为直接左递归
def is_indirect_zdg(grammars):
for p in grammars:
left=p[:p.find('-')]
right=p[p.find('>')+1:].split('|')
#判断right中是否有res的第一个字符是非终结符且等于left,若有则停止迭代,调用直接左递归函数进行消除,否则继续迭代
i=0
num = 0
while(i<len(right)):
res=right[i]
# if 'A' <= res[0] <= 'Z' and res[0] == left and num == 0:
# print('存在直接左递归')
if 'A' <= res[0] <= 'Z' and res[0] == left and num != 0:
print('存在间接左递归,已经将间接左递归转换成直接左递归')
print('调用消除直接左递归的函数进行消除')
#给出目前的规则p(即要进行消除的规则p)
new_p=left+'->'+'|'.join(right)
grammars[grammars.index(p)]=new_p
print('转换成的直接左递归文法:')
print_grammars(grammars)
while('A' <= res[0] <= 'Z' and res[0] != left):
num+=1
#继续迭代:从right中找到第一个字符是非终结符的res,进而找到该非终结符产生的规则,将其右边带入res中该非终结符的位置,完成一次迭代
target_right=grammars_dict[res[0]]#要被带入原规则中的结果
new_res=[]
for r in target_right:
new_res.append(r+res[1:])
if res in right:
right.remove(res)
i-=1
right+=new_res
break
i+=1
if num+1 == len(grammars):
break
else:
print('不存在间接左递归')
# 测试
is_indirect_zdg(grammars)说明:本代码将间接左递归转成直接左递归后,需要手动将结果粘贴到消除直接左递归的文件中进行运行 测试。不过,在最后的全部代码整理中,会实现自动调用的功能,无需手动。
测试例子结果截图:

3 消除无用符号
代码:
'''
1、消除无用符号:
无用符号包括:(1)非产生符号 (2)不可达符号(即推不出终结符号)
约定:非终结符是A-Z,终结符是a-z
'''
#输出文法,格式规范化
def print_grammars(grammars:list):
for p in grammars:
print(p)
return
grammars=['S->aAD','A->bBb','D->cD|c','E->ab','B->N', 'N->dN|$'] # 测试消除非产生符号 师姐
# grammars=['S->a|aA|E','A->aA|bA|B|$','B->aC','C->a|b|aC|bC','D->a|aD|cD','E->aEc|Eac']
print('上下文无关文法:')
print_grammars(grammars)
print('-----------------------------------------------------------------------')
# 消除无用符号(不可达符号)
def delete(grammars):
oldV=[]
newV=[]
for p in grammars: #对于文法grammars中的每条规则
right=p[(p.find('-')+2):]
left=p[:p.find('-')]
res=right.split('|')
#如果列表res中存在全由终结符号或$构成的字符串,则说明这条规则左侧的非终结符是可达的,就将该非终结符放到newV中
for rs in res:
reach=True
for char in rs:
if (char < 'a' or char > 'z') and char != '$':
reach=False
break
if reach==True and left not in newV:
newV.append(left)
print('初始状态的可达非终结符列表:',newV)
while(oldV != newV):#得到所有可达的非终结符
oldV=newV
add=[]
for p in grammars: # 对于文法grammars中的每条规则
right = p[(p.find('-') + 2):] # 每条规则中箭头右边的部分
# print('right:',right)
res = right.split('|') # 每条规则中,左侧非终结符可以推出的式子(不唯一,以|分割),结果是一个列表
# print('res:',res)
# 如果列表res中存在全由终结符号构成的字符串,则说明这条规则左侧的非终结符是可达的,就将该非终结符放到newV中
for re in res:
reach = True
for char in re:
if (char < 'a' or char > 'z') and (char not in oldV):
reach = False
break
if reach == True and p[:p.find('-')] not in add:
add.append(p[:p.find('-')])
# print('add:',add)
newV=list(set(newV+add))
print('最终状态的可达非终结符列表:',newV)#存放所有可达的非终结符
# 找到所有需要的非终结符
all=[]
for i in grammars:
id = i.find('-')
L = i[:id]
if L not in all:
all.insert(len(all), L)
# print('all:',all)
# 删掉所有不可达终结符的产生式(即产生式的左边是不可达终结符)
for i in all:
if i not in newV:
for j in grammars:
id = j.find('-')
L = j[:id]
if L == i:
grammars.remove(j)
# print('grammars:',grammars)
return grammars
res1=delete(grammars)
print("消除不可达非终结符后的结果:")
print_grammars(res1)
print('-----------------------------------------------------------------------')
# 消除无用符号(非产生符号)
def delete_useless(grammars):
use=['S']
all=[]
# 找到所有产生式中有用的非终结符
for i in grammars:
id=i.find('-')
L=i[:id]
if L in use:
for j in i:
if 'A'<=j<='Z' and j not in use:
use.insert(len(use),j)
#找到所有需要的非终结符
for i in grammars:
id=i.find('-')
L=i[:id]
if L not in all:
all.insert(len(all),L)
#删除无用符号及其产生式
for i in all:
if i not in use:
for j in grammars:
id=j.find('-')
L=j[:id]
if L==i:
grammars.remove(j)
return grammars
res2=delete_useless(res1)
print('消除非产生符号后的结果:')
print_grammars(res2)
print('-----------------------------------------------------------------------')
print('消除无用符号及其产生式后的结果:')
print_grammars(res2)
print('-----------------------------------------------------------------------')测试例子结果截图:

4 消除单一产生式
代码:
'''
2、消除单一产生式
(1)判断是否存在单一产生式 (2)消除单一产生式
'''
#输出文法,格式规范化
def print_grammars(grammars:list):
for p in grammars:
print(p)
return
grammars=['S->aAD','A->bBb','D->cD|c','B->N', 'N->dN|$']
# grammars=['S->ACA','A->aAa|B','B->bB|b|C','C->Cc|$']
# grammars=['S->ACA','A->aAa|B','B->bB|b|C','C->Cc|D|$','D->ad']
# grammars=['S->aAbBC','A->aA|B|$','B->bcB|Cca','C->cC|c']
print('上下文无关文法:')
print_grammars(grammars)
print('-----------------------------------------------------------------------')
#判断文法grammas中是否存在单一产生式,如果存在则将单一产生式加入列表single中
def is_single(grammars):
single=[]
flag=False
for p in grammars:
right=p[p.find('>')+1:].split('|')
for res in right:
if len(res)==1 and 'A' <= res <= 'Z':
flag=True
single.append(p)
return flag,single
flag,single=is_single(grammars)
print('是否存在单一产生式:',is_single(grammars)) #(True, ['B->N'])
def delete_single(grammars,single):
all_left=[p[:p.find('-')] for p in grammars]#存放文法gramms中所有规则的左部,便于后面遍历规则的左边寻找用于替换的规则
i=0
while(i<len(single)):
p=single[i]
right=p[p.find('>')+1:].split('|')
for res in right:
if len(res) == 1 and 'A' <= res <= 'Z':
old_right=res #单一产生式的右边,即需要被替换的非终结符
dest_p=grammars[all_left.index(old_right)]#根据规则的左部找到目标规则
if dest_p not in single:
#进行替换
right[right.index(res)]=dest_p[dest_p.find('>')+1:]#需要替换的结果=目标产生式的右部
new_p=p[:p.find('-')] + '->' + '|'.join(right) #新的规则 = 原来的左部 + 新的右部
grammars[all_left.index(p[:p.find('-')])]=new_p #更新文法grammars中的单一产生式
i+=1
# print(grammars)
flag1,single1=is_single(grammars)
if flag1 == True:
delete_single(grammars,single1)
return grammars
if flag==True:
print('消除单一产生式后的文法:')
print_grammars(delete_single(grammars,single))
print('-----------------------------------------------------------------------')测试例子结果截图:


5 消除空产生式
代码:
'''
3、消除空产生式
(1)判断是否存在空产生式(即遍历产生式,看是否存在eposilou,代码中用'$'代替) (2)消除空产生式
'''
#输出文法,格式规范化
def print_grammars(grammars:list):
for p in grammars:
print(p)
return
grammars=['S->aAD','A->bBb','D->cD|c','B->dN|$', 'N->dN|$']
# grammars=['S->AB','A->aAb|aA|$','B->bB|C', 'C->cC|$']
# grammars=['S->aAbBC', 'A->aA|bcB|Cca|$', 'B->bcB|Cca', 'C->cC|c']
print('上下文无关文法:')
print_grammars(grammars)
print('-----------------------------------------------------------------------')
#判断文法grammars中是否存在空产生式,如果存在,返回可空非终结符列表new_V0
def is_empty(grammars):
#得到初始的new_V0
new_V0 =[]
for p in grammars:
right=p[p.find('>')+1:].split('|')
left=p[:p.find('-')]
if '$' in right and left not in new_V0:
new_V0.append(left)
# print(new_V0)
old_V0=[]
while(old_V0 != new_V0):
old_V0=new_V0
for p in grammars:#如果A-》X,(X是单个非终结符,)且X在old_V0中,就将left放到new_V0中
right = p[p.find('>') + 1:].split('|')
left = p[:p.find('-')]
for V in old_V0:
if V in right and left not in new_V0:
new_V0.append(left)
# print(new_V0)
for p in grammars:#如果A-》X,X由多个old_V0中的非终结符构成,就将left放到new_V0中
right = p[p.find('>') + 1:].split('|')
left = p[:p.find('-')]
for res in right:
flag=True
for char in res:
if char not in old_V0:
flag=False
break
if flag==True and len(res) != 1:
new_V0.append(left)
# print('new_V0:',new_V0)
# print('new_V0:',new_V0)
return (new_V0!=[]),new_V0
flag,new_V0=is_empty(grammars)
print('是否存在空产生式:',flag)
print('可空非终结符列表:',new_V0)
#遍历文法,找到右部结果中包含new_V0中非终结符的规则,在结果中新增用$代替非终结符的情况,更新文法
def delete_empty(grammars,new_V0):
m_grammars=[]#需要修改的规则集合
for p in grammars:#找到右部结果中包含new_V0中非终结符的规则(即可空非终结符所在规则 都要对其进行修改)
right=p[p.find('>')+1:].split('|')
for res in right:
for V in new_V0:
if V in res and p not in m_grammars:
m_grammars.append(p)
# print('m_grammars:',m_grammars)
rest_grammars=[]#文法grammars中剩余不需要修改的规则集合
for p in grammars:
if p not in m_grammars and p not in rest_grammars:
rest_grammars.append(p)
# print('rest_grammars:',rest_grammars)
#消除空产生式
for p in m_grammars:
right = p[p.find('>') + 1:].split('|')
# print(right)
left = p[:p.find('-')]
for res in right:
num=0 #首先对结果res中的可空非终结符计数
can_kong=[]
for char in res:
if char in new_V0:
num+=1
can_kong.append(char)
if num > 1:#如果结果res中的可空非终结符不止一个,那就对于res中存在的每个可空非终结符,使其等于空,产生一个新结果加入结果列表right中
# print('res:',res)
for char in can_kong:
rs=res.replace(char,'')
if (rs != '' and rs not in right) or (rs == '' and left == 'S' and rs not in right):
right.append(rs)
if rs == '$':#将原本包含$的产生式的右部结果列表中的$删掉
right.remove(rs)
else:#如果结果res中的可空非终结符只有一个
for V in new_V0:#将需要修改的规则中的可空非终结符用$代替(体现在代码中就是用''代替),并将新增加的结果情况添加到结果列表right中
if V in res:
res=res.replace(V,'')
if (res != '' and res not in right) or (res == '' and left == 'S' and res not in right):
right.append(res)
if res == '$':#将原本包含$的产生式的右部结果列表中的$删掉
right.remove(res)
# print('right:',right)
if left=='S' and '' in right:#如果是S->'',那就可以保留这条规则,要将''转换成$
right[right.index('')]='$'
new_p=left+'->'+'|'.join(right)#新规则 = 左部 + '->' + 右部结果列表用'|'连接得到的字符串
# print(new_p)
m_grammars[m_grammars.index(p)]=new_p#用新规则替换m_grammars列表中的旧规则,得到更新后的规则列表
# print(m_grammars)
grammars=rest_grammars+m_grammars#消除空产生式后的文法 = 不需要修改的规则 + 更新后的规则
return grammars
if flag==True:
print('消除空产生式后的结果:')
print_grammars(delete_empty(grammars,new_V0))
print('-----------------------------------------------------------------------')测试例子结果截图:

6 得到Greibach范式
代码:
'''
5、生成Greibach范式
假设文法grammars是右线性文法,即文法每条规则右部都是以终结符开头的。
'''
import random
#输出文法,格式规范化
def print_grammars(grammars:list):
for p in grammars:
print(p)
return
grammars=['S->aAD','D->cD|c','A->bBb|bb','B->dN|d','N->dN|d']
# grammars=['B->bcB|Cca', 'C->cC|c', 'S->aAbBC|abBC', 'A->aA|bcB|Cca|a']
print('上下文无关文法:')
print_grammars(grammars)
print('-----------------------------------------------------------------------')
#将grammars由列表形式转换为字典形式,其中key为产生式的左边,value为产生式的右边的结果列表
grammars_dict=dict()
for p in grammars:
left = p[:p.find('-')]
right = p[p.find('>') + 1:].split('|')
grammars_dict[left]=right
print('grammars_dict:',grammars_dict)
#判断是否需要先对文法进行化简(即:看是否存在结果中第一个字符是非终结符的规则,若存在则需要先进行化简,否则直接生成Greibach范式即可)
def need_hj(grammars):
flag=False
hj_grammars=[]
for p in grammars:
right=p[p.find('>')+1:].split('|')
for res in right:
if 'A' <= res[0] <= 'Z':
flag=True
if p not in hj_grammars:
hj_grammars.append(p)
return flag,hj_grammars
flag,hj_grammars=need_hj(grammars)
print('是否需要先进行化简?',flag)
# print('需要进行化简的产生式列表:',hj_grammars)
#需要化简话,进行化简
def hj(grammars,hj_grammars):
for p in hj_grammars:
right=p[p.find('>')+1:].split('|')
left=p[:p.find('-')]
for res in right:
if 'A' <= res[0] <= 'Z':#要在grammars中找到res[0]产生的式子,并用其右边代替res[0]的位置
target_res_ls=grammars_dict[res[0]]#['cC', 'c']
# print('target_res_ls:',target_res_ls)
new_res=[res.replace(res[0],rs) for rs in target_res_ls]
# print('new_res:',new_res)#['cCca', 'cca']
if res in right:
right.remove(res)
for rs in new_res:
if rs not in right:
right.append(rs)
# print('new_right:',right)
new_p=left+'->'+'|'.join(right)
# print('new_p:',new_p)
grammars[grammars.index(p)]=new_p
# print(grammars)
return grammars
if flag == True:
grammars=hj(grammars,hj_grammars)
print('化简后的文法:')
print_grammars(grammars)
print('-----------------------------------------------------------------------')
#统计规则中的所有出现过的非终结符
def count_V(grammars):
used_V=''
for p in grammars:
for char in p:
if char in 'ABCDEFGHIJKLMNOPQRSTUVWXYZ' and char not in used_V:
used_V+=char
return used_V
used_V=count_V(grammars)
# print('文法grammars中出现过的所有非终结符:',used_V)
available_V=''
for char in 'ABCDEFGHIJKLMNOPQRSTUVWXYZ':
if char not in used_V:
available_V+=char
# print('没有出现在文法grammars中的所有可用非终结符:',available_V)
#根据value找到列表中对应的规则p
def get_p(ls,char):
ls_dict=dict()
for p in ls:
right=p[p.find('>')+1:]
left=p[:p.find('-')]
ls_dict[left]=right
for k,v in ls_dict.items():
if v==char:
return k+'->'+v
else:
return ''
#生成Greibach范式
def get_Greibach(grammars):
add_grammars = []#存放增加的产生式
for p in grammars:
right=p[p.find('>')+1:].split('|')
left=p[:p.find('-')]
# print('right:',right)
j=0
while(j<len(right)):
res=right[j]
for i in range(len(res[1:])):
if res[1:][i].islower():#如果结果从第2个字符开始的字符串中存在终结符,要用新的非终结符进行替换,并生成新的产生式
# print('判别:',get_p(add_grammars,res[1:][i]))
if get_p(add_grammars,res[1:][i]) == '':#如果add_grammars中已经存在能推出该终结符的产生式,那就不用在产生新的非终结符,用该产生式的左部即可
new_V=random.choice(available_V)
# new_V='T'
else:
new_V=get_p(add_grammars, res[1:][i])[0]
new_grammars=new_V+'->'+res[1:][i]
if new_grammars not in add_grammars:
add_grammars.append(new_grammars)
res=res[:i+1]+new_V+res[i+2:]#更新结果
# print('new_res:',res)
right[j]=res#用更新后的结果替换结果列表中原来的结果
# print('right:',right)
j+=1
# print('最后的right:',right)
# print('add_grammars:',add_grammars)
new_p=left+'->'+'|'.join(right)#依据更新后的结果列表得到更新后的产生式
# print('new_p:',new_p)
grammars[grammars.index(p)]=new_p#更新文法
# print('grammars:',grammars)
# print('最后的add_grammars:',add_grammars)
for p in add_grammars:#将增加的产生式追加到文法中得到最终的文法
if p not in grammars:
grammars.append(p)
# print('最终的grammars:',grammars)
return grammars
print('生成的Greibach范式:')
print_grammars(get_Greibach(grammars))
print('-----------------------------------------------------------------------')
测试例子结果截图:


7 生成状态转移函数
代码:
'''
6、由Greibach范式生成状态转移函数
'''
#输出文法,格式规范化
def print_grammars(grammars:list):
for p in grammars:
print(p)
return
grammars=['S->aAD','D->cD|c','A->bBT|bT','B->dN|d','N->dN|d','T->b']
# grammars=['B->bPB|cCPN|cPN', 'C->cC|c', 'S->aAOBC|aOBC', 'A->aA|bPB|a|cCPN|cPN', 'P->c', 'N->a', 'O->b']
# grammars=['S->aAFBC|aFBC|bDBC|bBC|dBC|dGC','F->a','G->d','A->aAF|aF|bD|b','D->bD|b','B->dB|dG','C->eCG|eHGG','H->e']
print('Greibach范式:')
print_grammars(grammars)
print('-----------------------------------------------------------------------')
#生成状态转移函数
def get_ztzy(grammars):
ztzy_grammars=dict()#用于存放所有的状态转移函数,key为状态转移函数等号的左边,数据类型是str,数据类型是str,value为状态转移函数等号的右边,数据类型为list,列表中的元素是str
ztzy_grammars['f(q0,$,z)']=['(q1,Sz)']#初始状态转移函数
ztzy_grammars['f(q1,$,z)']=['(qf,z)']#终止状态转移函数
for p in grammars:
right=p[p.find('>')+1:].split('|')
left=p[:p.find('-')]
for res in right:
current_char=res[:1]#当前读入的字符
# print(current_char)
current_state=left#当前栈顶状态
trans_str=res[1:]#转移字符串
if trans_str == '':
trans_str='$'
key='f(q1,'+current_char+','+current_state+')'
value=[]
value.append('(q1,'+trans_str+')')
# print('key:',key)
# print('value:',value)
if key in ztzy_grammars.keys():
ztzy_grammars[key]+=value
else:
ztzy_grammars[key]=value
# print(ztzy_grammars.items())
# print(len(ztzy_grammars.keys()))
return ztzy_grammars
ztzy_grammars=get_ztzy(grammars)
# print('状态转移函数:',ztzy_grammars.items())
#输出函数,修改输出格式
def output(dict:dict):
for key in dict.keys():
str=key+'={'+','.join(dict[key])+'}'
print(str)
print('生成的状态转移函数:')
output(ztzy_grammars)
print('-----------------------------------------------------------------------')
测试例子结果截图:

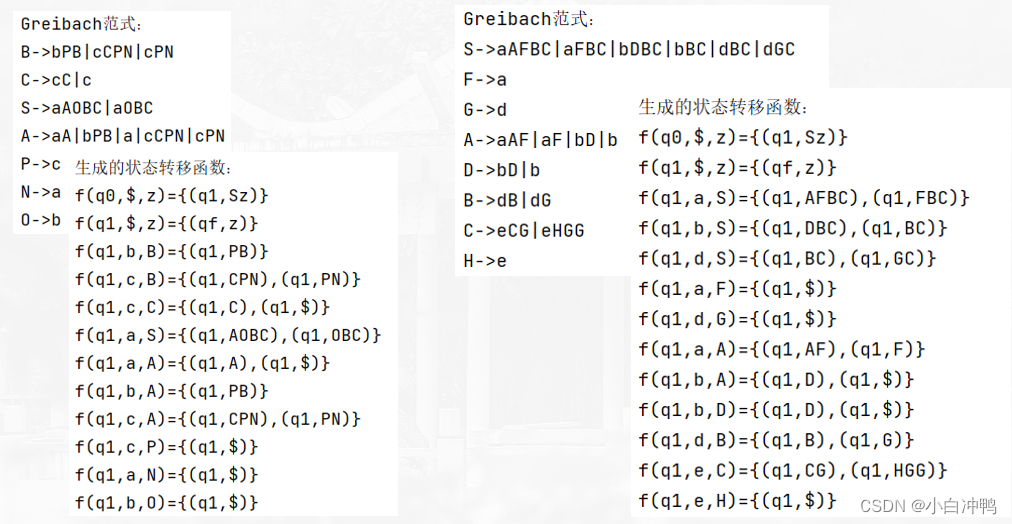
8 得到下推自动机NPDA
代码:
'''
7、根据状态转移函数得到下推自动机NPDA,识别句子是否属于该文法
'''
ztzy_grammars={'f(q0,$,z)':['(q1,Sz)'],
'f(q1,$,z)':['(qf,z)'],
'f(q1,a,S)':['(q1,AD)'],
'f(q1,c,D)':['(q1,D)','(q1,$)'],
'f(q1,b,A)':['(q1,BT)','(q1,T)'],
'f(q1,d,B)':['(q1,N)','(q1,$)'],
'f(q1,d,N)':['(q1,N)','(q1,$)'],
'f(q1,b,T)':['(q1,$)']
}
# ztzy_grammars={
# 'f(q0,$,z)':['(q1,Sz)'],
# 'f(q1,$,z)':['(qf,z)'],
# 'f(q1,b,B)':['(q1,PB)'],
# 'f(q1,c,B)':['(q1,CPN)','(q1,PN)'],
# 'f(q1,c,C)':['(q1,C)','(q1,$)'],
# 'f(q1,a,S)':['(q1,AOBC)','(q1,OBC)'],
# 'f(q1,a,A)':['(q1,A)','(q1,$)'],
# 'f(q1,b,A)':['(q1,PB)'],
# 'f(q1,c,A)':['(q1,CPN)','(q1,PN)'],
# 'f(q1,c,P)':['(q1,$)'],
# 'f(q1,a,N)':['(q1,$)'],
# 'f(q1,b,O)':['(q1,$)']
# }
# sentence='abdbcc'
# sentence='acc'
# sentence='abddddd'
sentence='AB'
print('测试句子:',sentence)
#下推自动机函数
def npda(sentence,ztzy_grammars):
#先检查句子中是否有不是小写字母的字符,若有直接返回 不可以接受该句子
for char in sentence:
if char not in 'abcdefghijklmnopqrstuvwxyz':
return '不能接受该句子'
#若句子中的字符均符合要求(即都是小写字母),则进行初始化操作
char_ls=[]#用于存放读入的字符,便于回溯
stack_ls=['z']#用于存放当前栈顶元素,便于回溯
state_ls=[]#用于记录当前状态,便于回溯
poped_stack_ls=[]#用于记录出栈元素
enter_stack_ls=[]#用于记录入栈的逆序转移字符串
keys = ztzy_grammars.keys()
values = [0] * len(ztzy_grammars.keys())
key_num = {k: v for k, v in zip(keys, values)} # 用于记录每条状态函数使用的次数
#1、初始状态函数
state_ls.append('q0')
char_ls.append('$')
current_state=state_ls[0]
current_char=char_ls[0]
current_stack_top=stack_ls[0]
key='f('+current_state+','+current_char+','+current_stack_top+')'
# print('key:',key)
if key in ztzy_grammars.keys():
key_num[key]+=1
value=ztzy_grammars[key]
# print('value:',value)
j=key_num[key]-1
if j > len(value) - 1:
return '不能接受该句子'
# print(value[j])
current_state=value[j][1:value[j].index(',')]#1、更新当前的状态
state_ls.append(current_state)#2、将更新的状态加入状态列表中
trans_str=value[j][value[j].index(',')+1:-1]#3、当前的转移字符
poped_stack_ls.append(stack_ls[-1])#4、将栈顶元素加入出栈元素列表中
stack_ls.pop()#5、弹出栈顶元素
enter_stack_ls.append(trans_str[::-1])
for char in trans_str[::-1]:#6、将转移字符逆序压入栈中
stack_ls.append(char)
current_stack_top=stack_ls[-1]#7、更新当前栈顶元素
current_char=sentence[0]#8、更新当前读入的字符
# print('初始状态转移函数:')
# print('当前的状态:',current_state,'\n下一个要读入的字符:',current_char,'\n当前的栈顶元素:',current_stack_top)#q1 a S
# print('当前的状态列表:',state_ls,'\n当前读入的字符列表:',char_ls,'\n当前的栈中元素列表:',stack_ls,'\n当前的出栈元素列表:',poped_stack_ls,'\n当前入栈的逆序转移字符串列表:',enter_stack_ls)
# print()
#2、开始读入句子中的第一个字符,对于句子中的每个字符
i=0
flag = False
while i < len(sentence):
key='f('+current_state+','+current_char+','+current_stack_top+')'
# print('key:',key)#f(q1,a,S)
if key in ztzy_grammars.keys():#如果状态转移函数中存在以key为左边的函数,那就根据函数进行操作,否则回溯
key_num[key]+=1
value=ztzy_grammars[key]#根据当前的状态、读入的字符和当前栈顶元素,在状态转移函数字典中由key得到对应的value列表
# print('value:',value)
# print('current_char:',current_char)
if current_char == char_ls[-1] and flag==False:#当句子中存在连续重复字符时,如果没有经历回退操作,就取状态函数值列表中的第一个
key_num[key]-=1
j=key_num[key]-1
else:
j=key_num[key]-1
flag=False
# print('key_num[key]:',key_num[key])
if j > len(value)-1:
return '不能接受该句子'
# print(value[j])
current_state=value[j][1:value[j].index(',')]#1、更新当前的状态
state_ls.append(current_state)#2、将更新后的状态加入状态列表中
poped_stack_ls.append(stack_ls[-1])#3、将栈顶元素加入出栈元素列表中
stack_ls.pop()#4、弹出栈顶元素
trans_str=value[j][value[j].index(',')+1:-1]#5(1)、获取转移字符
enter_stack_ls.append(trans_str[::-1])
if trans_str != '$':#当转移字符不为空时,将转移字符逆序压入栈中
for char in trans_str[::-1]:#5(2)、将转移字符串逆序压入栈中
stack_ls.append(char)
current_stack_top=stack_ls[-1]#6、更新栈顶元素指针
char_ls.append(current_char)#7、将当前读入字符加入到读入字符列表中
i=i+1
if i>=len(sentence):
current_char='$'
else:
current_char=sentence[i]#8、更新当前读入元素
# print('当前的状态:', current_state, '\n下一个要读入的字符:', current_char, '\n当前的栈顶元素:', current_stack_top)
# print('当前的状态列表:', state_ls, '\n当前读入的字符列表:', char_ls, '\n当前的栈中元素列表:', stack_ls,'\n当前的出栈元素列表:',poped_stack_ls,'\n当前入栈的逆序转移字符串列表:',enter_stack_ls)
if 'f('+current_state+','+current_char+','+current_stack_top+')' not in ztzy_grammars.keys():
flag = True
# print('重复字符:状态转移函数中没有以key为左边的函数,请回溯到上一步')
# 回退到上一步的状态
state_ls.pop() # 1、将新加入的状态删掉
current_state = state_ls[-1] # 2、当前状态等于状态列表中的最后一个状态
current_char = char_ls[-1] # 3、当前读入字符等于读入字符列表中的最后一个字符
char_ls.pop() # 4、删掉读入字符列表中的最后一个字符
trans_str_prev = enter_stack_ls[-1] # 获取上一步入栈的字符串
enter_stack_ls.pop()
for num in range(len(trans_str_prev)): # 将上一步入栈的字符串出栈
stack_ls.pop()
current_stack_top = poped_stack_ls[-1] # 3、将删掉的栈顶元素恢复
stack_ls.append(current_stack_top)
poped_stack_ls.pop() # 4、删掉出栈元素列表中的最后一个(考虑过程可以发现每次都是弹出一个栈顶元素,所以这里也是删掉一个)元素
# print('当前的状态:', current_state, '\n下一个要读入的字符:', current_char, '\n当前的栈顶元素:', current_stack_top)
# print('当前的状态列表:', state_ls, '\n当前读入的字符列表:', char_ls, '\n当前的栈中元素列表:', stack_ls, '\n当前的出栈元素列表:',
# poped_stack_ls, '\n当前入栈的逆序转移字符串列表:', enter_stack_ls)
i = i - 1
else:
# print('状态转移函数中没有以key为左边的函数,请回溯到上一步')
#回退到上一步的状态
state_ls.pop()#1、将新加入的状态删掉
current_state=state_ls[-1]#2、当前状态等于状态列表中的最后一个状态
current_char=char_ls[-1]#3、当前读入字符等于读入字符列表中的最后一个字符
char_ls.pop()#4、删掉读入字符列表中的最后一个字符
trans_str_prev=enter_stack_ls[-1]#获取上一步入栈的字符串
enter_stack_ls.pop()
for num in range(len(trans_str_prev)):#将上一步入栈的字符串出栈
stack_ls.pop()
current_stack_top=poped_stack_ls[-1]#3、将删掉的栈顶元素恢复
stack_ls.append(current_stack_top)
poped_stack_ls.pop()#4、删掉出栈元素列表中的最后一个(考虑过程可以发现每次都是弹出一个栈顶元素,所以这里也是删掉一个)元素
# print('当前的状态:', current_state, '\n下一个要读入的字符:', current_char, '\n当前的栈顶元素:', current_stack_top)
# print('当前的状态列表:', state_ls, '\n当前读入的字符列表:', char_ls, '\n当前的栈中元素列表:', stack_ls, '\n当前的出栈元素列表:',poped_stack_ls,'\n当前入栈的逆序转移字符串列表:',enter_stack_ls)
i=i-1
#3、读完字符串后,判断最后的状态是否能推出终态。如果能推出终态,则该句子可接受,否则不可接受
# print('\n读完句子的最终状态:')
# print('当前的状态:', current_state, '\n下一个要读入的字符:', current_char, '\n当前的栈顶元素:', current_stack_top)
# print('当前的状态列表:', state_ls, '\n当前读入的字符列表:', char_ls, '\n当前的栈中元素列表:', stack_ls, '\n当前的出栈元素列表:', poped_stack_ls,'\n当前入栈的逆序转移字符串列表:', enter_stack_ls)
key = 'f(' + current_state + ',' + current_char + ',' + current_stack_top + ')'
if key in ztzy_grammars.keys():
value=ztzy_grammars[key]
current_state=value[0][1:value[0].index(',')]
if current_state =='qf':
# print('可以推出终态:')
# print('当前的状态:', current_state, '\n下一个要读入的字符:', current_char, '\n当前的栈顶元素:', current_stack_top)
# print('当前的状态列表:', state_ls, '\n当前读入的字符列表:', char_ls, '\n当前的栈中元素列表:', stack_ls, '\n当前的出栈元素列表:',poped_stack_ls, '\n当前入栈的逆序转移字符串列表:', enter_stack_ls)
return '可以接受该句子'
else:
return '不能接受该句子'
else:
return '不能接受该句子'
result=npda(sentence,ztzy_grammars)
print(result)
另外,本文给出第一个例子(abdbcc)的具体推导过程的截图:











?


全部代码
import random
'''
1 消除左递归
(1)直接左递归 (2)间接左递归
'''
##########--(1)--直接左递归----###########
#判断是否存在直接左递归
def is_direct_zdg(grammars):
flag=False
direct_zdg_grammars=[]
for p in grammars:#遍历文法grammars中的每条规则,如果右部结果列表中某个结果的首字母=左部,那么这条规则就包含直接左递归,将该规则放到direct_zdg_grammars中
right=p[p.find('>')+1:].split('|')
left=p[:p.find('-')]
for res in right:
if res != '$' and res[0]==left:
direct_zdg_grammars.append(p)
flag=True
# print(direct_zdg_grammars)
if flag==True:
return flag,direct_zdg_grammars
else:
return flag
#统计文法中的所有出现过的非终结符
def count_V(grammars):
used_V=''
for p in grammars:
for char in p:
if char in 'ABCDEFGHIJKLMNOPQRSTUVWXYZ' and char not in used_V:
used_V+=char
return used_V
#得到可用的非终结符
def get_avail_V(grammars:list):
used_V=count_V(grammars)
available_V=''
for char in 'ABCDEFGHIJKLMNOPQRSTUVWXYZ':
if char not in used_V:
available_V+=char
return available_V
#消除直接左递归
def delete_direct_zdg(grammars,direct_zdg_grammars):
available_V=get_avail_V(grammars)
#找到不包含直接左递归的规则集合
rest_grammars=[]
for p in grammars:
if p not in direct_zdg_grammars and p not in rest_grammars:
rest_grammars.append(p)
# print('不包含直接左递归的规则集合:',rest_grammars)
for p in direct_zdg_grammars:
new_V=random.choice(available_V)#从没有出现过的可用非终结符中随机挑选一个非终结符作为新的V
right=p[p.find('>')+1:].split('|')
left=p[:p.find('-')]
#找到结果列表right中首字符不是left的结果
res_first_not_left=[res for res in right if res[0]!=left]
if '$' in res_first_not_left:
res_first_not_left[res_first_not_left.index('$')]=''
# print('规则右部结果中首字母不是左部的结果有:',res_first_not_left)
#找到结果列表中第一个字母是left的结果,除第一个字母外的剩余部分rest_sec
rest_sec=[]
for res in right:
if res[0]==left:
rest_sec.append(res[1:])
# print('结果除第一个字母外的剩余部分:',rest_sec)
new_p_ls = []
new_p1=left+'->'+'|'.join([char+new_V for char in res_first_not_left])
# print('消除直接左递归产生的第一个式子:',new_p1)
new_p2=new_V+'->'+'|'.join([char+new_V for char in rest_sec]+['$'])
# print('消除直接左递归产生的第二个式子:',new_p2)
new_p_ls.append(new_p1)
new_p_ls.append(new_p2)
#将消除直接左递归产生的两个式子加入到grammars中,更新gramms
grammars=rest_grammars+new_p_ls
return grammars
##########--(2)--间接左递归----###########
#将grammars由列表形式转换为字典形式,其中key为产生式的左边,value为产生式的右边的结果列表
def ls2dict(grammars:list):
grammars_dict=dict()
for p in grammars:
left = p[:p.find('-')]
right = p[p.find('>') + 1:].split('|')
grammars_dict[left]=right
# print(grammars_dict)
return grammars_dict
#若存在间接左递归则转换成直接左递归并进行消除,否则输出“不存在间接左递归”
#判断是否存在间接左递归:把一个式子迭代到底,如果存在间接左递归,那就直接将间接左递归转换为直接左递归
def is_indirect_zdg(grammars:list):
grammars_dict=ls2dict(grammars)
for p in grammars:
left=p[:p.find('-')]
right=p[p.find('>')+1:].split('|')
#判断right中是否有res的第一个字符是非终结符且等于left,若有则停止迭代,调用直接左递归函数进行消除,否则继续迭代
i=0
num = 0
while(i<len(right)):
res=right[i]
# if 'A' <= res[0] <= 'Z' and res[0] == left and num == 0:
# print('存在直接左递归')
if 'A' <= res[0] <= 'Z' and res[0] == left and num != 0:
print('存在间接左递归,已经将间接左递归转换成直接左递归')
print('调用消除直接左递归的函数进行消除')
#给出目前的规则p(即要进行消除的规则p)
new_p=left+'->'+'|'.join(right)
grammars[grammars.index(p)]=new_p
print('转换成的直接左递归文法:')
print_grammars(grammars)
#消除直接左递归
_,direct_zdg_grammars=is_direct_zdg(grammars)
delete_direct_zdg(grammars,direct_zdg_grammars)
while('A' <= res[0] <= 'Z' and res[0] != left):
num+=1
#继续迭代:从right中找到第一个字符是非终结符的res,进而找到该非终结符产生的规则,将其右边带入res中该非终结符的位置,完成一次迭代
target_right=grammars_dict[res[0]]#要被带入原规则中的结果
new_res=[]
for r in target_right:
new_res.append(r+res[1:])
if res in right:
right.remove(res)
i-=1
right+=new_res
break
i+=1
if num+1 == len(grammars):
break
else:
print('不存在间接左递归')
'''
2 消除无用符号
(1)不可达符号 (2)非产生符号
'''
##########--(1)--不可达符号----###########
# 消除无用符号(不可达符号)
def delete(grammars):
oldV=[]
newV=[]
for p in grammars: #对于文法grammars中的每条规则
right=p[(p.find('-')+2):]
left=p[:p.find('-')]
res=right.split('|')
#如果列表res中存在全由终结符号或$构成的字符串,则说明这条规则左侧的非终结符是可达的,就将该非终结符放到newV中
for rs in res:
reach=True
for char in rs:
if (char < 'a' or char > 'z') and char != '$':
reach=False
break
if reach==True and left not in newV:
newV.append(left)
# print('初始状态的可达非终结符列表:',newV)
while(oldV != newV):#得到所有可达的非终结符
oldV=newV
add=[]
for p in grammars: # 对于文法grammars中的每条规则
right = p[(p.find('-') + 2):] # 每条规则中箭头右边的部分
# print('right:',right)
res = right.split('|') # 每条规则中,左侧非终结符可以推出的式子(不唯一,以|分割),结果是一个列表
# print('res:',res)
# 如果列表res中存在全由终结符号构成的字符串,则说明这条规则左侧的非终结符是可达的,就将该非终结符放到newV中
for re in res:
reach = True
for char in re:
if (char < 'a' or char > 'z') and (char not in oldV):
reach = False
break
if reach == True and p[:p.find('-')] not in add:
add.append(p[:p.find('-')])
# print('add:',add)
newV=list(set(newV+add))
# print('最终状态的可达非终结符列表:',newV)#存放所有可达的非终结符
# 找到所有需要的非终结符
all=[]
for i in grammars:
id = i.find('-')
L = i[:id]
if L not in all:
all.insert(len(all), L)
# print('all:',all)
# 删掉所有不可达终结符的产生式(即产生式的左边是不可达终结符)
for i in all:
if i not in newV:
for j in grammars:
id = j.find('-')
L = j[:id]
if L == i:
grammars.remove(j)
# print('grammars:',grammars)
return grammars
##########--(2)--非产生符号----###########
# 消除无用符号(非产生符号)
def delete_useless(grammars):
use=['S']
all=[]
# 找到所有产生式中有用的非终结符
for i in grammars:
id=i.find('-')
L=i[:id]
if L in use:
for j in i:
if 'A'<=j<='Z' and j not in use:
use.insert(len(use),j)
#找到所有需要的非终结符
for i in grammars:
id=i.find('-')
L=i[:id]
if L not in all:
all.insert(len(all),L)
#删除无用符号及其产生式
for i in all:
if i not in use:
for j in grammars:
id=j.find('-')
L=j[:id]
if L==i:
grammars.remove(j)
return grammars
# 消除无用符号
def delete_wyfh(grammars:list):
res1=delete(grammars)
res2=delete_useless(res1)
return res2
'''
3 消除单一产生式
(1)判断是否存在 (2)进行消除
'''
##########--(1)--判断是否存在----###########
#判断文法grammas中是否存在单一产生式,如果存在则将单一产生式加入列表single中
def is_single(grammars):
single=[]
flag=False
for p in grammars:
right=p[p.find('>')+1:].split('|')
for res in right:
if len(res)==1 and 'A' <= res <= 'Z':
flag=True
single.append(p)
return flag,single
##########--(2)--进行消除----###########
# 消除单一产生式
def delete_single(grammars,single):
all_left=[p[:p.find('-')] for p in grammars]#存放文法gramms中所有规则的左部,便于后面遍历规则的左边寻找用于替换的规则
i=0
while(i<len(single)):
p=single[i]
right=p[p.find('>')+1:].split('|')
for res in right:
if len(res) == 1 and 'A' <= res <= 'Z':
old_right=res #单一产生式的右边,即需要被替换的非终结符
dest_p=grammars[all_left.index(old_right)]#根据规则的左部找到目标规则
if dest_p not in single:
#进行替换
right[right.index(res)]=dest_p[dest_p.find('>')+1:]#需要替换的结果=目标产生式的右部
new_p=p[:p.find('-')] + '->' + '|'.join(right) #新的规则 = 原来的左部 + 新的右部
grammars[all_left.index(p[:p.find('-')])]=new_p #更新文法grammars中的单一产生式
i+=1
# print(grammars)
flag1,single1=is_single(grammars)
if flag1 == True:
delete_single(grammars,single1)
return grammars
# 消除单一产生式
def delete_single_grammars(grammars:list):
flag,single=is_single(grammars)
if flag==True:
grammars=delete_single(grammars,single)
return grammars
'''
4 消除空产生式
(1)判断是否存在 (2)进行消除
'''
##########--(1)--判断是否存在----###########
#判断文法grammars中是否存在空产生式,如果存在,返回可空非终结符列表new_V0
def is_empty(grammars):
#得到初始的new_V0
new_V0 =[]
for p in grammars:
right=p[p.find('>')+1:].split('|')
left=p[:p.find('-')]
if '$' in right and left not in new_V0:
new_V0.append(left)
# print(new_V0)
old_V0=[]
while(old_V0 != new_V0):
old_V0=new_V0
for p in grammars:#如果A-》X,(X是单个非终结符,)且X在old_V0中,就将left放到new_V0中
right = p[p.find('>') + 1:].split('|')
left = p[:p.find('-')]
for V in old_V0:
if V in right and left not in new_V0:
new_V0.append(left)
# print(new_V0)
for p in grammars:#如果A-》X,X由多个old_V0中的非终结符构成,就将left放到new_V0中
right = p[p.find('>') + 1:].split('|')
left = p[:p.find('-')]
for res in right:
flag=True
for char in res:
if char not in old_V0:
flag=False
break
if flag==True and len(res) != 1:
new_V0.append(left)
# print('new_V0:',new_V0)
# print('new_V0:',new_V0)
return (new_V0!=[]),new_V0
##########--(2)--进行消除----###########
# 消除空产生式
#遍历文法,找到右部结果中包含new_V0中非终结符的规则,在结果中新增用$代替非终结符的情况,更新文法
def delete_empty(grammars,new_V0):
m_grammars=[]#需要修改的规则集合
for p in grammars:#找到右部结果中包含new_V0中非终结符的规则(即可空非终结符所在规则 都要对其进行修改)
right=p[p.find('>')+1:].split('|')
for res in right:
for V in new_V0:
if V in res and p not in m_grammars:
m_grammars.append(p)
# print('m_grammars:',m_grammars)
rest_grammars=[]#文法grammars中剩余不需要修改的规则集合
for p in grammars:
if p not in m_grammars and p not in rest_grammars:
rest_grammars.append(p)
# print('rest_grammars:',rest_grammars)
#消除空产生式
for p in m_grammars:
right = p[p.find('>') + 1:].split('|')
# print(right)
left = p[:p.find('-')]
for res in right:
num=0 #首先对结果res中的可空非终结符计数
can_kong=[]
for char in res:
if char in new_V0:
num+=1
can_kong.append(char)
if num > 1:#如果结果res中的可空非终结符不止一个,那就对于res中存在的每个可空非终结符,使其等于空,产生一个新结果加入结果列表right中
# print('res:',res)
for char in can_kong:
rs=res.replace(char,'')
if (rs != '' and rs not in right) or (rs == '' and left == 'S' and rs not in right):
right.append(rs)
if rs == '$':#将原本包含$的产生式的右部结果列表中的$删掉
right.remove(rs)
else:#如果结果res中的可空非终结符只有一个
for V in new_V0:#将需要修改的规则中的可空非终结符用$代替(体现在代码中就是用''代替),并将新增加的结果情况添加到结果列表right中
if V in res:
res=res.replace(V,'')
if (res != '' and res not in right) or (res == '' and left == 'S' and res not in right):
right.append(res)
if res == '$':#将原本包含$的产生式的右部结果列表中的$删掉
right.remove(res)
# print('right:',right)
if left=='S' and '' in right:#如果是S->'',那就可以保留这条规则,要将''转换成$
right[right.index('')]='$'
new_p=left+'->'+'|'.join(right)#新规则 = 左部 + '->' + 右部结果列表用'|'连接得到的字符串
# print(new_p)
m_grammars[m_grammars.index(p)]=new_p#用新规则替换m_grammars列表中的旧规则,得到更新后的规则列表
# print(m_grammars)
grammars=rest_grammars+m_grammars#消除空产生式后的文法 = 不需要修改的规则 + 更新后的规则
return grammars
# 消除空产生式
def delete_empty_grammars(grammars:list):
flag,new_V0=is_empty(grammars)
if flag==True:
grammars=delete_empty(grammars,new_V0)
return grammars
'''
5 生成Greibach范式
(1)判断是否需要化简 (2)生成Greibach范式
'''
##########--(1)--判断是否需要化简----###########
#判断是否需要先对文法进行化简(即:看是否存在结果中第一个字符是非终结符的规则,若存在则需要先进行化简,否则直接生成Greibach范式即可)
def need_hj(grammars):
flag=False
hj_grammars=[]
for p in grammars:
right=p[p.find('>')+1:].split('|')
for res in right:
if 'A' <= res[0] <= 'Z':
flag=True
if p not in hj_grammars:
hj_grammars.append(p)
return flag,hj_grammars
#需要化简话,进行化简
def hj(grammars,hj_grammars):
grammars_dict=ls2dict(grammars)
for p in hj_grammars:
right=p[p.find('>')+1:].split('|')
left=p[:p.find('-')]
for res in right:
if 'A' <= res[0] <= 'Z':#要在grammars中找到res[0]产生的式子,并用其右边代替res[0]的位置
target_res_ls=grammars_dict[res[0]]#['cC', 'c']
# print('target_res_ls:',target_res_ls)
new_res=[res.replace(res[0],rs) for rs in target_res_ls]
# print('new_res:',new_res)#['cCca', 'cca']
if res in right:
right.remove(res)
for rs in new_res:
if rs not in right:
right.append(rs)
# print('new_right:',right)
new_p=left+'->'+'|'.join(right)
# print('new_p:',new_p)
grammars[grammars.index(p)]=new_p
# print(grammars)
return grammars
#根据value找到列表中对应的规则p
def get_p(ls,char):
ls_dict=dict()
for p in ls:
right=p[p.find('>')+1:]
left=p[:p.find('-')]
ls_dict[left]=right
for k,v in ls_dict.items():
if v==char:
return k+'->'+v
else:
return ''
##########--(2)--生成Greibach范式----###########
#生成Greibach范式
def get_Greibach(grammars):
available_V=get_avail_V(grammars)
add_grammars = []#存放增加的产生式
for p in grammars:
right=p[p.find('>')+1:].split('|')
left=p[:p.find('-')]
# print('right:',right)
j=0
while(j<len(right)):
res=right[j]
for i in range(len(res[1:])):
if res[1:][i].islower():#如果结果从第2个字符开始的字符串中存在终结符,要用新的非终结符进行替换,并生成新的产生式
# print('判别:',get_p(add_grammars,res[1:][i]))
if get_p(add_grammars,res[1:][i]) == '':#如果add_grammars中已经存在能推出该终结符的产生式,那就不用在产生新的非终结符,用该产生式的左部即可
new_V=random.choice(available_V)
# new_V='T'
else:
new_V=get_p(add_grammars, res[1:][i])[0]
new_grammars=new_V+'->'+res[1:][i]
if new_grammars not in add_grammars:
add_grammars.append(new_grammars)
res=res[:i+1]+new_V+res[i+2:]#更新结果
# print('new_res:',res)
right[j]=res#用更新后的结果替换结果列表中原来的结果
# print('right:',right)
j+=1
# print('最后的right:',right)
# print('add_grammars:',add_grammars)
new_p=left+'->'+'|'.join(right)#依据更新后的结果列表得到更新后的产生式
# print('new_p:',new_p)
grammars[grammars.index(p)]=new_p#更新文法
# print('grammars:',grammars)
# print('最后的add_grammars:',add_grammars)
for p in add_grammars:#将增加的产生式追加到文法中得到最终的文法
if p not in grammars:
grammars.append(p)
# print('最终的grammars:',grammars)
return grammars
# 生成Greibach范式
def Greibach(grammars:list):
flag,hj_grammars=need_hj(grammars)
if flag==True:# 如果需要化简,则先对文法进行化简
grammars = hj(grammars, hj_grammars)
grammars=get_Greibach(grammars)
return grammars
'''
6 生成状态转移函数
'''
#生成状态转移函数
def get_ztzy(grammars):
ztzy_grammars=dict()#用于存放所有的状态转移函数,key为状态转移函数等号的左边,数据类型是str,数据类型是str,value为状态转移函数等号的右边,数据类型为list,列表中的元素是str
ztzy_grammars['f(q0,$,z)']=['(q1,Sz)']#初始状态转移函数
ztzy_grammars['f(q1,$,z)']=['(qf,z)']#终止状态转移函数
for p in grammars:
right=p[p.find('>')+1:].split('|')
left=p[:p.find('-')]
for res in right:
current_char=res[:1]#当前读入的字符
# print(current_char)
current_state=left#当前栈顶状态
trans_str=res[1:]#转移字符串
if trans_str == '':
trans_str='$'
key='f(q1,'+current_char+','+current_state+')'
value=[]
value.append('(q1,'+trans_str+')')
# print('key:',key)
# print('value:',value)
if key in ztzy_grammars.keys():
ztzy_grammars[key]+=value
else:
ztzy_grammars[key]=value
# print(ztzy_grammars.items())
# print(len(ztzy_grammars.keys()))
return ztzy_grammars
#输出函数,修改输出格式
def ztzy_func_output(dict:dict):
for key in dict.keys():
str=key+'={'+','.join(dict[key])+'}'
print(str)
'''
7 得到下推自动机NPDA
'''
#下推自动机函数
def npda(sentence,ztzy_grammars):
#先检查句子中是否有不是小写字母的字符,若有直接返回 不可以接受该句子
for char in sentence:
if char not in 'abcdefghijklmnopqrstuvwxyz':
return '不能接受该句子'
#若句子中的字符均符合要求(即都是小写字母),则进行初始化操作
char_ls=[]#用于存放读入的字符,便于回溯
stack_ls=['z']#用于存放当前栈顶元素,便于回溯
state_ls=[]#用于记录当前状态,便于回溯
poped_stack_ls=[]#用于记录出栈元素
enter_stack_ls=[]#用于记录入栈的逆序转移字符串
keys = ztzy_grammars.keys()
values = [0] * len(ztzy_grammars.keys())
key_num = {k: v for k, v in zip(keys, values)} # 用于记录每条状态函数使用的次数
#1、初始状态函数
state_ls.append('q0')
char_ls.append('$')
current_state=state_ls[0]
current_char=char_ls[0]
current_stack_top=stack_ls[0]
key='f('+current_state+','+current_char+','+current_stack_top+')'
# print('key:',key)
if key in ztzy_grammars.keys():
key_num[key]+=1
value=ztzy_grammars[key]
# print('value:',value)
j=key_num[key]-1
if j > len(value) - 1:
return '不能接受该句子'
# print(value[j])
current_state=value[j][1:value[j].index(',')]#1、更新当前的状态
state_ls.append(current_state)#2、将更新的状态加入状态列表中
trans_str=value[j][value[j].index(',')+1:-1]#3、当前的转移字符
poped_stack_ls.append(stack_ls[-1])#4、将栈顶元素加入出栈元素列表中
stack_ls.pop()#5、弹出栈顶元素
enter_stack_ls.append(trans_str[::-1])
for char in trans_str[::-1]:#6、将转移字符逆序压入栈中
stack_ls.append(char)
current_stack_top=stack_ls[-1]#7、更新当前栈顶元素
current_char=sentence[0]#8、更新当前读入的字符
# print('初始状态转移函数:')
# print('当前的状态:',current_state,'\n下一个要读入的字符:',current_char,'\n当前的栈顶元素:',current_stack_top)#q1 a S
# print('当前的状态列表:',state_ls,'\n当前读入的字符列表:',char_ls,'\n当前的栈中元素列表:',stack_ls,'\n当前的出栈元素列表:',poped_stack_ls,'\n当前入栈的逆序转移字符串列表:',enter_stack_ls)
# print()
#2、开始读入句子中的第一个字符,对于句子中的每个字符
i=0
flag = False
while i < len(sentence):
key='f('+current_state+','+current_char+','+current_stack_top+')'
# print('key:',key)#f(q1,a,S)
if key in ztzy_grammars.keys():#如果状态转移函数中存在以key为左边的函数,那就根据函数进行操作,否则回溯
key_num[key]+=1
value=ztzy_grammars[key]#根据当前的状态、读入的字符和当前栈顶元素,在状态转移函数字典中由key得到对应的value列表
# print('value:',value)
# print('current_char:',current_char)
if current_char == char_ls[-1] and flag==False:#当句子中存在连续重复字符时,如果没有经历回退操作,就取状态函数值列表中的第一个
key_num[key]-=1
j=key_num[key]-1
else:
j=key_num[key]-1
flag=False
# print('key_num[key]:',key_num[key])
if j > len(value)-1:
return '不能接受该句子'
# print(value[j])
current_state=value[j][1:value[j].index(',')]#1、更新当前的状态
state_ls.append(current_state)#2、将更新后的状态加入状态列表中
poped_stack_ls.append(stack_ls[-1])#3、将栈顶元素加入出栈元素列表中
stack_ls.pop()#4、弹出栈顶元素
trans_str=value[j][value[j].index(',')+1:-1]#5(1)、获取转移字符
enter_stack_ls.append(trans_str[::-1])
if trans_str != '$':#当转移字符不为空时,将转移字符逆序压入栈中
for char in trans_str[::-1]:#5(2)、将转移字符串逆序压入栈中
stack_ls.append(char)
current_stack_top=stack_ls[-1]#6、更新栈顶元素指针
char_ls.append(current_char)#7、将当前读入字符加入到读入字符列表中
i=i+1
if i>=len(sentence):
current_char='$'
else:
current_char=sentence[i]#8、更新当前读入元素
# print('当前的状态:', current_state, '\n下一个要读入的字符:', current_char, '\n当前的栈顶元素:', current_stack_top)
# print('当前的状态列表:', state_ls, '\n当前读入的字符列表:', char_ls, '\n当前的栈中元素列表:', stack_ls,'\n当前的出栈元素列表:',poped_stack_ls,'\n当前入栈的逆序转移字符串列表:',enter_stack_ls)
if 'f('+current_state+','+current_char+','+current_stack_top+')' not in ztzy_grammars.keys():
flag = True
# print('重复字符:状态转移函数中没有以key为左边的函数,请回溯到上一步')
# 回退到上一步的状态
state_ls.pop() # 1、将新加入的状态删掉
current_state = state_ls[-1] # 2、当前状态等于状态列表中的最后一个状态
current_char = char_ls[-1] # 3、当前读入字符等于读入字符列表中的最后一个字符
char_ls.pop() # 4、删掉读入字符列表中的最后一个字符
trans_str_prev = enter_stack_ls[-1] # 获取上一步入栈的字符串
enter_stack_ls.pop()
for num in range(len(trans_str_prev)): # 将上一步入栈的字符串出栈
stack_ls.pop()
current_stack_top = poped_stack_ls[-1] # 3、将删掉的栈顶元素恢复
stack_ls.append(current_stack_top)
poped_stack_ls.pop() # 4、删掉出栈元素列表中的最后一个(考虑过程可以发现每次都是弹出一个栈顶元素,所以这里也是删掉一个)元素
# print('当前的状态:', current_state, '\n下一个要读入的字符:', current_char, '\n当前的栈顶元素:', current_stack_top)
# print('当前的状态列表:', state_ls, '\n当前读入的字符列表:', char_ls, '\n当前的栈中元素列表:', stack_ls, '\n当前的出栈元素列表:',
# poped_stack_ls, '\n当前入栈的逆序转移字符串列表:', enter_stack_ls)
i = i - 1
else:
# print('状态转移函数中没有以key为左边的函数,请回溯到上一步')
#回退到上一步的状态
state_ls.pop()#1、将新加入的状态删掉
current_state=state_ls[-1]#2、当前状态等于状态列表中的最后一个状态
current_char=char_ls[-1]#3、当前读入字符等于读入字符列表中的最后一个字符
char_ls.pop()#4、删掉读入字符列表中的最后一个字符
trans_str_prev=enter_stack_ls[-1]#获取上一步入栈的字符串
enter_stack_ls.pop()
for num in range(len(trans_str_prev)):#将上一步入栈的字符串出栈
stack_ls.pop()
current_stack_top=poped_stack_ls[-1]#3、将删掉的栈顶元素恢复
stack_ls.append(current_stack_top)
poped_stack_ls.pop()#4、删掉出栈元素列表中的最后一个(考虑过程可以发现每次都是弹出一个栈顶元素,所以这里也是删掉一个)元素
# print('当前的状态:', current_state, '\n下一个要读入的字符:', current_char, '\n当前的栈顶元素:', current_stack_top)
# print('当前的状态列表:', state_ls, '\n当前读入的字符列表:', char_ls, '\n当前的栈中元素列表:', stack_ls, '\n当前的出栈元素列表:',poped_stack_ls,'\n当前入栈的逆序转移字符串列表:',enter_stack_ls)
i=i-1
#3、读完字符串后,判断最后的状态是否能推出终态。如果能推出终态,则该句子可接受,否则不可接受
# print('\n读完句子的最终状态:')
# print('当前的状态:', current_state, '\n下一个要读入的字符:', current_char, '\n当前的栈顶元素:', current_stack_top)
# print('当前的状态列表:', state_ls, '\n当前读入的字符列表:', char_ls, '\n当前的栈中元素列表:', stack_ls, '\n当前的出栈元素列表:', poped_stack_ls,'\n当前入栈的逆序转移字符串列表:', enter_stack_ls)
key = 'f(' + current_state + ',' + current_char + ',' + current_stack_top + ')'
if key in ztzy_grammars.keys():
value=ztzy_grammars[key]
current_state=value[0][1:value[0].index(',')]
if current_state =='qf':
# print('可以推出终态:')
# print('当前的状态:', current_state, '\n下一个要读入的字符:', current_char, '\n当前的栈顶元素:', current_stack_top)
# print('当前的状态列表:', state_ls, '\n当前读入的字符列表:', char_ls, '\n当前的栈中元素列表:', stack_ls, '\n当前的出栈元素列表:',poped_stack_ls, '\n当前入栈的逆序转移字符串列表:', enter_stack_ls)
return '可以接受该句子'
else:
return '不能接受该句子'
else:
return '不能接受该句子'
#输出文法,格式规范化
def print_grammars(grammars:list):
for p in grammars:
print(p)
return
if __name__ == '__main__':
file='./input.txt'
grammars=[]
with open(file,'r') as fp:
line=fp.readline()
while line!= '':
grammars.append(line[:-1])
line = fp.readline()
fp.close()
print('上下文无关文法:')
print_grammars(grammars)
# 上下文无关文法----->Greibach范式
# 1 消除左递归
_,direct_zdg_grammars=is_direct_zdg(grammars)
grammars=delete_direct_zdg(grammars,direct_zdg_grammars)
print('消除左递归后:')
print_grammars(grammars)
# 2 消除无用符号
grammars=delete_wyfh(grammars)
print('消除无用符号后:')
print_grammars(grammars)
# 3 消除单一产生式
grammars=delete_single_grammars(grammars)
print('消除单一产生式后:')
print_grammars(grammars)
# 4 消除空产生式
grammars=delete_empty_grammars(grammars)
print('消除空产生式后:')
print_grammars(grammars)
# 5 生成Greibach范式
grammars=Greibach(grammars)
print('生成Greibach范式:')
print_grammars(grammars)
# Greibach范式------>下推自动机NPDA
# 6 生成状态转移函数
ztzy_grammars = get_ztzy(grammars)
print('生成状态转移函数:')
ztzy_func_output(ztzy_grammars)
# 7 得到下推自动机NPDA
# sentence=input('请输入测试句子:')
sentence='abdbcc'
# sentence='acc'
# sentence='abddddd'
# sentence = 'AB'
result = npda(sentence, ztzy_grammars)
print(result)
到此,由上下文无关文法到Greibach范式,再到下推自动机NPDA的全部过程、算法、代码、例子就都讲解完了,希望能够帮助到大家呀~
?
?
文章来源:https://blog.csdn.net/m0_56367027/article/details/135313563
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!