机器学习（四） -- 模型评估（3）

系列文章目录

机器学习（一） -- 概述

机器学习（二） -- 数据预处理（1-3）

机器学习（三） -- 特征工程（1-2）

机器学习（四） -- 模型评估（1-4）

未完待续……

目录

机器学习（四） -- 模型评估（1）

机器学习（四） -- 模型评估（2）

---

系列文章目录

前言

四、?回归模型评估指标

1、均方误差（Mean Squared Error，MSE）

2、***均方根误差（Root?Mean Squared Error，RMSE）

3、***均方对数误差（Mean Squared Log Error，MSLE）

4、平均绝对误差（Mean Absolute Error，MAE）

5、***平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）

6、决定系数（R2，R-square）

7、***校正决定系数（Adjusted R-square）

---

机器学习（四） -- 模型评估（4）

前言

tips：这里只是总结，不是教程哈。

“***”开头的是给好奇心重的宝宝看的，其实不太重要可以跳过。

此处以下所有内容均为暂定，因为我还没找到一个好的，让小白（我自己）也能容易理解（更系统、嗯应该是宏观）的讲解顺序与方式。

第一文主要简述了一下机器学习大致有哪些东西（当然远远不止这些），对大体框架有了一定了解。接着我们根据机器学习的流程一步步来学习吧，掐掉其他不太用得上我们的步骤，精练起来就4步（数据预处理，特征工程，训练模型，模型评估），其中训练模型则是我们的重头戏，基本上所有算法也都是这一步，so，这个最后写，先把其他三个讲了，然后，在结合这三步来进行算法的学习，兴许会好点（个人拙见）。

衡量模型泛化能力的评价标准就是性能度量（模型评估指标、模型评价标准），而针对不同的任务有不同的评价指标。按照数据集的目标值不同，可以把模型评估分为分类模型评估、回归模型评估和聚类模型评估。

四、?回归模型评估指标

均方误差（MSE）、均方根误差（RMSE）、均方对数误差（MSLE）、
平均绝对误差（MAE）??????、平均绝对百分比误差（MAPE）、
决定系数（R2，R-square）、校正决定系数（Adjusted R-square）

1、均方误差（Mean Squared Error，MSE）

回归任务最常用的性能度量就是均方误差。是预测数据和原始数据对应点误差的平方和的均值。越小越好。

公式：

?

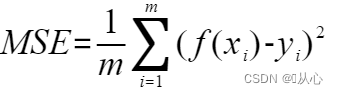均方误差存在一个明显的缺陷，
假设，现在有三个样本，它们的预测值与真实值的差分别为 3、4、5，通过均方误差的计算公式，我们可以分别计算出这三个样本的误差为 9、16 和 25；第三个样本的误差等于前两个样本的误差和，也就是说样本的预测值离真实值越远，误差也越大，且增长幅度越来越大。

模型为了降低误差，势必会想办法优先让偏差最大的样本尽可能靠近真实值。换言之，偏差越大的样本对模型的影响也越大，如果这个样本是噪声，那么这对模型的精度产生重大负面影响。简单地说，均方误差对噪声不鲁棒。【鲁棒性（robustness）是指系统或者算法在不同的情况下，仍能够保持稳定和可靠的能力。】

就像我们再【数据预处理（2）的2.1.3、3σ法则】中遇到的情况一样噪声数据影响过大。

API：

from sklearn.metrics import mean_squared_error

我们用波士顿房价数据集为例，模型选择决策树算法，来测试。

import numpy as np
from sklearn.datasets import load_boston
from sklearn.tree import DecisionTreeRegressor
from sklearn.model_selection import train_test_split


# 引入数据集
boston = load_boston()

# 划分数据集
x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, test_size=0.3, random_state=134)

#模型训练
model = DecisionTreeRegressor()
model.fit(x_train, y_train)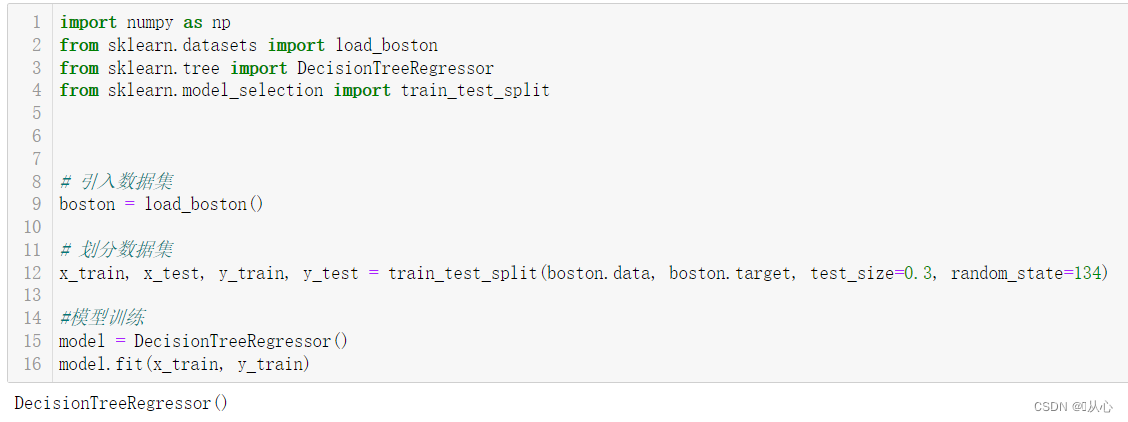

?

from sklearn.metrics import mean_squared_error

# 均方误差
mean_squared_error(y_test, model.predict(x_test))

??

2、***均方根误差（Root?Mean Squared Error，RMSE）

均方误差开根号。

和MSE一样，对异常点（outliers）较敏感，如果回归器对某个点的回归值很不理性，那么它的误差则较大，从而会对RMSE的值有较大影响，即平均值是非鲁棒的。

公式：

?

代码：

代码也很简单，上面那个开个平方就好了。?

# 均方根误差
np.sqrt(mean_squared_error(y_test, model.predict(x_test)))

?

3、***均方对数误差（Mean Squared Log Error，MSLE）

公式：

?

代码：

from sklearn.metrics import mean_squared_log_error

# 均方对数误差
mean_squared_log_error(y_test, model.predict(x_test))

?

4、平均绝对误差（Mean Absolute Error，MAE）

公式：

?

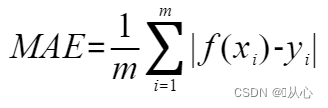代码：

from sklearn.metrics import mean_absolute_error

# 平均绝对误差
mean_absolute_error(y_test, model.predict(x_test))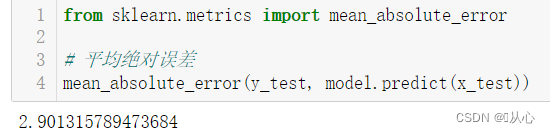

?

5、***平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）

公式：

?

代码：

from sklearn.metrics import mean_absolute_percentage_error

# 平均绝对百分比误差
mean_absolute_percentage_error(y_test, model.predict(x_test))

?

6、决定系数（R2，R-square）

反映因变量的全部变异能通过回归关系被自变量解释的比例。拟合优度越大，自变量对因变量的解释程度越高，自变量引起的变动占总变动的百分比越高，观察点在回归直线附近越密集。
决定系数R2越高，越接近于1，模型的拟合效果就越好。

公式：S^2是方差

?

代码：

from sklearn.metrics import r2_score

# 决定系数
r2_score(y_test, model.predict(x_test))

?

7、***校正决定系数（Adjusted R-square）

公式：

?

代码：

r2=r2_score(y_test, model.predict(x_test))

n, p = x_test.shape
adjusted_r2 = 1 - ((1 - r2) * (n - 1)) / (n - p - 1)
adjusted_r2

欲知后事如何，且看：机器学习（四） -- 模型评估（4）?