MnasNet: Platform-Aware Neural Architecture Search for Mobile(2019)

文章目录
原文链接
源代码
Abstract
存在的挑战
为移动设备设计卷积神经网络(CNN)具有挑战性,因为移动模型需要小而快,并且准确。尽管在设计和改进移动cnn方面已经付出了巨大的努力,但当有如此多的架构可能性需要考虑时,手动平衡这些权衡(准确性和延迟)是非常困难的
给出方法
在本文中,我们提出了一种自动移动神经架构搜索(MNAS)方法,该方法明确地将模型延迟纳入主要目标,以便搜索可以识别在准确性和延迟之间实现良好权衡的模型。
以往延迟是通过FLOPS(不准确的代理)来考虑的,而我们的方法通过在移动电话上执行模型直接测量现实世界的推理延迟
为了进一步在灵活性和搜索空间大小之间取得适当的平衡,我们提出了一种新的分层搜索空间,它鼓励整个网络中的层多样性
实验支撑
实验结果表明,我们的方法在多个视觉任务上始终优于最先进的移动CNN模型。在ImageNet分类任务上,我们的MnasNet在Pixel手机上以78ms的延迟实现了75.2%的top-1准确率,比MobileNetV2[29]快1.8倍,精度提高0.5%;比NASNet[36]快2.3倍,精度提高1.2%,我们的MnasNet在COCO对象检测方面也比MobileNets实现了更好的mAP质量
Introduction
目前的困境
随着CNN模型变得越来越深,越来越大,它们也变得越来越慢,需要更多的计算,因此很难部署到计算资源有限的平台如移动设备和嵌入设备
因此,最近的研究都集中在设计和改进移动CNN模型上,通过减少网络深度和使用更便宜的操作,如深度卷积和群卷积
然而,设计一个资源受限的移动模型是具有挑战性的:人们必须仔细平衡准确性和资源效率,这导致了一个非常大的设计空间。
给出的方法
我们提出了一种用于设计移动CNN模型的自动神经结构搜索方法

上图显示了我们的方法的概述,与以前的方法的主要区别在于延迟感知的多目标奖励和新的搜索空间。
我们的方法基于两个主要思想:
首先,我们将设计问题表示为一个多目标优化问题,同时考虑CNN模型的精度和推理延迟,此前方法用FLOPS来近似延迟,而我们是在移动设备上测量真实的延迟,该想法是受到FLOPS通常是一个不准确的代理的观察的启发:例如,MobileNet[11]和NASNet[36]具有相似的FLOPS,但它们的延迟差异很大(所以要勤于观察,善于发现)
其次,我们观察到以前的自动化方法(只搜索少数复杂的单元格,然后重复堆叠相同的单元格)排除了对计算效率很重要的层多样性。为了解决这个问题,我们提出了一种新的因式分层搜索空间,它允许层即使在架构上不同,但仍然能在灵活性和搜索空间大小之间取得适当的平衡
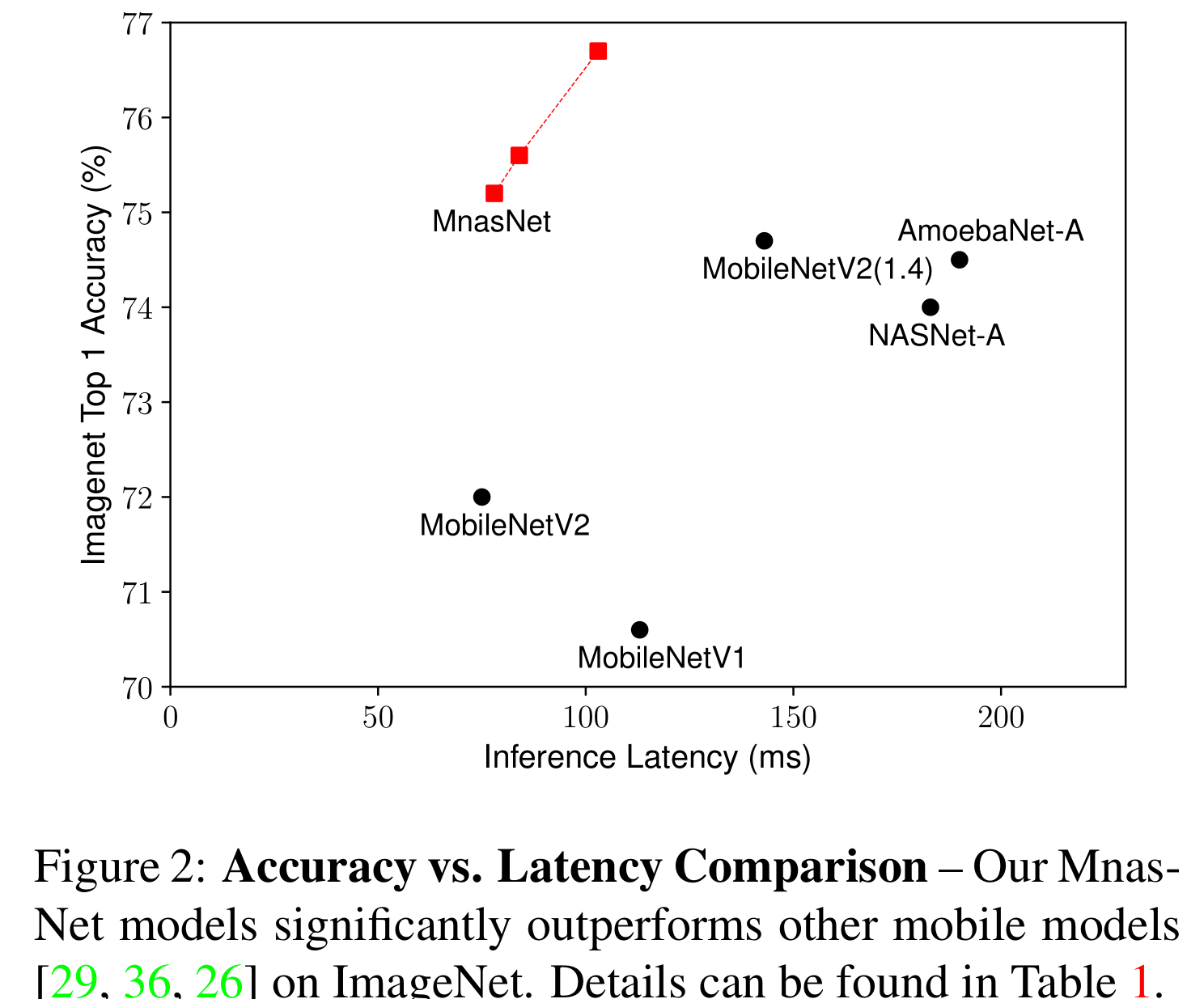
上图总结了MnasNet模型和其他最先进的移动模型之间的比较,显示了MnasNet模型的优越性
主要贡献
- 介绍了一种多目标神经结构搜索方法,该方法优化了移动设备上的准确性和真实世界的延迟。
- 提出了一种新的分解层次搜索空间,以实现层的多样性,同时在灵活性和搜索空间大小之间取得适当的平衡。
- 在典型的移动延迟约束下,我们在ImageNet分类和COCO目标检测上展示了新的最先进的精度。
Related Work
提高CNN模型的资源效率是一个活跃的研究课题,然而常用方法都与基线模型相关联,并不专注于学习CNN操作的新组合
另一种常见的方法是直接手工制作更高效的移动架构:SqueezeNet[15]通过使用更低成本的1x1卷积和减小滤波器尺寸来减少参数和计算的数量;MobileNet[11]广泛使用深度可分离卷积来最小化计算密度;ShuffleNets[33,24]利用低成本群卷积和信道shuffle;Condensenet[14]学习跨层连接群卷积;最近,MobileNetV2[29]通过使用资源高效的倒残差和线性瓶颈,在移动尺寸模型中获得了最先进的结果。不幸的是,考虑到潜在的巨大设计空间,这些手工制作的模型通常需要大量的人力
与我们的工作密切相关的是MONAS[12], DPP-Net [3], RNAS[34]和Pareto-NASH[4],它们在搜索cnn时试图优化多个目标,如模型大小和准确性,但它们的搜索过程在CIFAR等小任务上进行优化
相比之下,本文针对现实世界的移动延迟约束,并专注于更大的任务,如ImageNet分类和COCO目标检测
Problem Formulation
我们将设计问题描述为一个多目标搜索,旨在寻找具有高精度和低推理延迟的CNN模型。此前方法用FLOPS来近似延迟,而我们是在移动设备上测量真实的延迟,然后将真实世界的推理延迟合并到我们的目标中,从而考虑直接的现实世界推理延迟
给定模型m,设ACC(m)表示其在目标任务上的准确率,LAT(m)表示在目标移动平台上的推理延迟,T为目标延迟。一种常见的方法是将T视为硬约束,并在此约束下最大化精度:
然而,这种方法只能最大化单个度量,而不能提供多个帕累托最优解
我们使用自定义加权乘积法来逼近Pareto最优解,优化目标定义为:
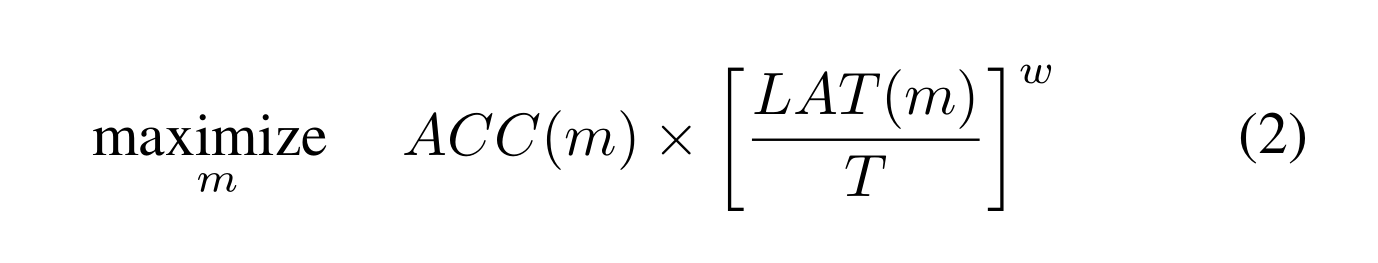
w是权重因子,定义为:
其中α和β是特定于应用程序的常数。考虑两个模型,M1延迟为l,精度为a,M2延迟为2l,精度为(1+5%)a,要让M1和M2得到相同的奖励,即a*(l/T)^β = (1+0.05)a*(2l/T)的β次方,可解得β≈-0.07,因此我们使用α = β = - 0.07
从上图中我们可以看到,在硬约束(top)条件下,当测量延迟大于目标延迟T时,我们会严厉惩罚目标值,以阻止模型违反延迟约束。而软约束条件下并不会
Mobile Neural Architecture Search
Factorized Hierarchical Search Space
定义良好的搜索空间对于神经结构搜索非常重要,然而,大多数先前的方法只搜索少数复杂的单元格,然后重复堆叠相同的单元格。这些方法不允许层多样性,而这对于实现高精度和低延迟至关重要。
因此,我们引入了一种新的分解层次搜索空间,它将CNN模型分解成独特的块,然后分别搜索每个块的操作和连接,从而允许在不同的块中使用不同的层架构。我们的直觉是,我们需要搜索基于输入和输出形状的最佳操作,以获得更好的精确延迟权衡。例如,cnn的早期阶段通常处理大量数据,因此对推理延迟的影响要比后期阶段大得多。
形式上,考虑一种广泛使用的深度可分离卷积[11]核,表示为四元组(K,K,M,N),它将大小为(H,W,M) 的输入转换为大小为(H,W,N)的输出,其中(H,W)为输入分辨率,M,N为输入/输出滤波器大小。乘加的总次数可以描述为:H ? W ? M ? (K ? K + N)

根据输入分辨率和过滤器大小,网络层被分成许多预定义的框架,称为块。每个块包含可变数量的重复相同层,如果输入/输出分辨率不同,则只有第一层具有步幅2,而所有其他层具有步幅1。对于每个块,我们搜索单个层的操作和连接以及层数N,然后同一层重复N次(例如,layer4-1到4- N4是相同的)。来自不同块的层(例如,层2-1和层4-1)可以是不同的。
上图显示了我们的搜索空间的基线架构,我们将CNN模型划分为一系列预定义的块,逐渐降低输入分辨率并增加过滤器大小。每个块都包含可变数量的重复相同层(layer4-1到4- N4是相同的),其操作和连接由每个块的子搜索空间决定。具体来说,块i的子搜索空间由以下选项组成:
?卷积运算ConvOp:常规conv (conv)、深度conv (dconv)和移动倒瓶颈conv[29]。
?卷积核大小KernelSize: 3x3, 5x5。
?挤压和激励比率:0,0.25。
?skip操作SkipOp:池化、身份残留或没有skip。
?输出滤波器大小F i。
?每个块的层数N i。
ConvOp, KernelSize, SERatio, SkipOp, F i决定了层的架构,N i决定了该层将为块重复多少次。
我们的分解层次搜索空间在平衡层的多样性和总搜索空间的大小方面具有明显的优势。假设我们将网络划分为B个块,每个块有一个大小为S的子搜索空间,每个块平均有N层,那么我们的总搜索空间大小将是S^B(因为来自同一块的不同层是重复的),平面逐层搜索空间大小为S的(B*N)次方。典型的情况是S = 432,B = 5,N = 3,其中我们的搜索空间大小约为10的13,平面逐层搜索空间大小为10的39
Search Algorithm
我们使用强化学习方法为我们的多目标搜索问题找到帕累托最优解
我们将搜索空间中的每个CNN模型映射到一个令牌列表,这些令牌由强化学习代理基于其参数θ的一系列动作a 1:T确定。我们的目标是最大化预期奖励: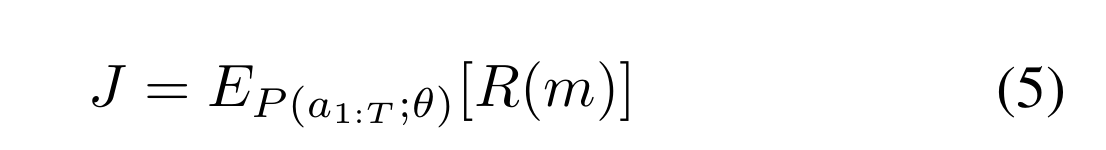
m是由作用a 1:T决定的抽样模型,R(m)是由自定义加权乘积法(式2)定义的目标值
如图所示,搜索框架由三个部分组成:基于循环神经网络(RNN)的控制器,用于获取模型精度的训练器,以及用于测量延迟的基于手机的推理引擎。我们遵循众所周知的采样-评估-更新循环来训练控制器。
在每一步中,1.控制器首先使用其当前参数θ对一批模型进行采样,通过基于其RNN的softmax logits预测一系列令牌。2.对于每个采样模型m,我们在目标任务上训练它得到它的准确率ACC(m),3.并在真实手机上运行它得到它的推理延迟LAT(m)。然后我们用等式2计算奖励值R(m)。在每一步结束时,通过使用邻域策略优化(Proximal Policy Optimization)最大化公式5定义的期望奖励来更新控制器的参数θ[30]。重复采样-求值-更新循环,直到达到最大步数或参数θ收敛
Experimental Setup
在本文中,我们直接在ImageNet训练集上执行架构搜索,但训练步骤较少(5个epoch)。作为一种常见的做法,我们从训练集中随机选择50K图像作为固定的验证集。为了确保准确度的提高来自我们的搜索空间,我们使用了与NASNet[36]相同的RNN控制器
Results
ImageNet Classification Performance

我们的Model在精度和速度上都展示了优越的性能,但需要注意到的是这里作者的MnasNet模型都是使用了SE块
该实验证实了即使未使用SE块,MnasNet性能依旧优于其他Model
Model Scaling Performance
两种常见的缩放技术:一是使用深度乘法器修改滤波器大小。例如,0.5的深度乘法器将每层中的通道数量减半,从而减少延迟和模型大小。二是在不改变网络的情况下减小输入图像的大小
图5通过改变深度乘法器和输入图像大小,比较了MnasNet和MobileNetV2的模型缩放性能。当我们将深度乘法器从0.35更改为1.4时,推理延迟也从20ms更改为160ms。如图5a所示,对于每个深度乘法器,我们的Mnas-Net模型始终比Mo- bileNetV2获得更好的精度。同样,我们的模型对输入尺寸的变化也很稳健,并且在从96到224的所有输入图像尺寸上始终优于MobileNetV2(精确度提高了4.1%),如图5b所示
除了模型缩放之外,我们的方法还允许为任何延迟目标搜索新架构。例如,一些视频应用程序可能需要低至25毫秒的延迟。我们可以缩小基线模型,或者搜索专门针对此延迟约束的新模型
在表4中,我们的MnasNet已经在相同的缩放参数下优于Mo-bileNetV2,但我们通过针对22ms延迟约束的新架构搜索进一步提高了准确性
COCO Object Detection Performance

Ablation Study and Discussion
Soft vs. Hard Latency Constraint

当α = 0,β = - 1时,延迟被视为硬约束,因此控制器倾向于更多地关注更快的模型以避免延迟惩罚。另一方面,通过设置α = β = -0.07,控制器将目标延迟视为软约束,并尝试在更宽的延迟范围内搜索模型。它在目标延迟值75ms周围采样更多模型,但也会探索延迟小于40ms或大于110ms的模型,这允许我们在单个架构搜索中从Pareto曲线中选择多个模型,如表1所示
Disentangling Search Space and Reward

该实验分别验证了所提出的搜索空间和多目标奖励对性能的影响,然后将两者结合起来,实现了更高的准确率和更低的延迟,表明了我们的搜索空间的有效性
MnasNet Architecture and Layer Diversity

MnasNet-A1模型架构如上图所示,MnasNet使用3×3卷积和5×5卷积,之前的移动模型仅使用3×3卷积
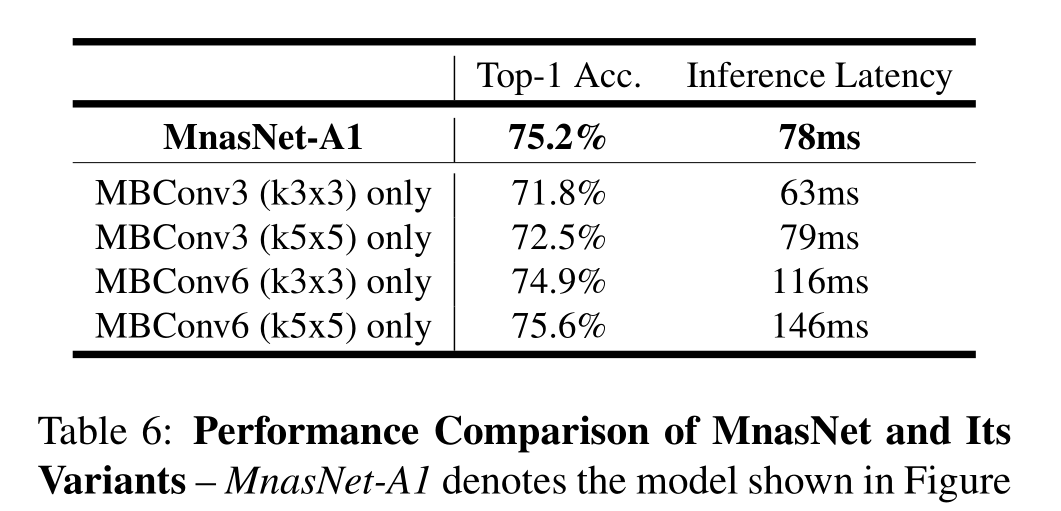
表6只重复单一类型的层(固定的内核大小和扩展比例),验证了层多样性对性能的重要性
Conclusion
本文提出了一种自动神经结构搜索方法,用于使用强化学习设计资源高效的移动CNN模型。主要思想是将平台感知的真实延迟信息整合到搜索过程中,并利用一种新的因式分层搜索空间来搜索具有准确性和延迟之间最佳权衡的移动模型
证明了该方法可以自动找到比现有方法更好的移动模型,并在典型的移动推理延迟约束下,在ImageNet分类和COCO对象检测上取得了新的最先进的结果
实验分别展示了提出的搜索空间和多目标奖励对性能的影响,并且两者结合实现了更高的准确率和更低的延迟,再一次表明了我们的搜索空间的有效性
由此产生的MnasNet架构证实了层多样性的重要性,这将指导我们设计和改进未来的移动CNN模型
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!