逻辑运算加法器

前言

逻辑门本质上操作的是单个二进制数，通过高低电压或者有无信号来表示，并且，因为二进制数的原因，一个数字，我们可以通过二进制数来表示，整数可以精确表示，浮点数可以近似表示
本篇文章使用逻辑门来构建加法器
git地址：https://gitlab.com/lingyanTools/comvirtual.git

加法器

先来看整数，一个二进制整数是怎么进行加法运算的呢？
看下面两个二进制数
$A=101（十进制）=01100101（二进制）$
$B=201（十进制）=11001001（二进制）$
我们从右边开始往左侧进行计算，计算相应的位，如果大于1，则进位，整个流程如下：

1. 默认进位是0
2. 1 + 1 + 进位0 = 0，进位1
3. 0 + 0 + 进位1 = 1，进位0
4. 1 + 0 + 进位0 = 1，进位0
5. 0 + 1 + 进位0 = 1，进位0
6. 0 + 0 + 进位0 = 0，进位0
7. 1 + 0 + 进位0 = 1，进位0
8. 1 + 1 + 进位0 = 0，进位1
9. 0 + 1 + 进位1 = 0，进位1

因为最后有个进位，所以最终的结果位100101110 = 302 = 101 + 201
很容易发现，对于二进制的加法的每一位操作，有两个值需要我们确定，一个是当前的进位值$C_i$，一个是当前的计算值$F_i$，可以用下面的公式表示：
$$\{\begin{array}{l}{F}_i=(X_i异或Y_i)异或C_{i?1},\\ C_i=(X_i与C_{i?1})或(Y_i与C_{i?1})或(X_i与Y_i)\end{array}$$

用电路表示$F_i$的值为：

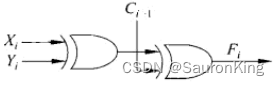
用电路表示$C_i$的值为：

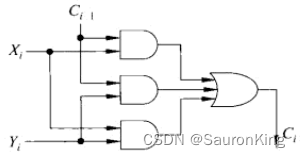
我们把通过输入$X_i$、$Y_i$和$C_{i?1}$获取输出$F_i $和$C_i$用C语言表示如下：

/**
 * 全加器
 * 输入两个二进制位，其实就是两根电路
 * 输入进位位：c
 * param:
 * f：输出值
 * c1:输出进位值
 * 返回加法位
 */
void full_add(long x,long y,long c,long* f, long* c1)
{
    long a = xor_gate(x, y);
    *f = xor_gate(a, c);
    
    long b1 = and_gate(x, c);
    long b2 = and_gate(y, c);
    long b3 = and_gate(x, y);
    *c1 = or_gate(or_gate(b1, b2),b3);
}

这个电路组合叫做全加器

串位进位加法器

上述的全加器可以计算一位的加法，我们把每位的运算连起来，就是我们上面计算过程列出的那样，从右向左依次计算，假设我们需要满足一个64位的加法器，我们可以用64个全加器串行连接起来，下图中n=64：

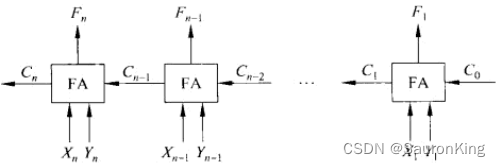
这种连接方式叫做串位进位加法器
这样我们的64位加法器就可以用C语言描述了

/**
 * 逻辑运算器的加法
 * param：
 * in_1：输入1
 * in_2：输入2
 * bits：选择执行加法的位数
 * 初始进位，并且返回执行后的进位
 * return: 返回输出结果
 */
long alu_add(long in_1, long in_2, long bits,long* c)
{
    long result = 0;
    for(int i = 0;i<bits;i++)
    {
        long x = alu_bit(in_1, i); // 获取输入1的第i位
        long y = alu_bit(in_2, i); // 获取输入2的第i位
        long f = 0;
        full_add(x, y, *c, &f, c);
        result |= f<<i;
    }
    return result;
}

/**
 * 获取二进制位
 * param：
 * in_1:输入的数据
 * bits:获取哪一位的二进制位,0~sizeof(long)-1
 * return
 * 返回获取到的数据0或1
 */
unsigned long alu_bit(unsigned long in_1, long bits)
{
    unsigned long a = 1;
    return ((a<<bits)&in_1)>>bits;
}

进位选择加法器

串位进位加法器由于是串行的，这就导致每一步的运算必须等待前面一位计算完成。几乎所有的算术运算都要用到ALU, ALU的核心还是加法器，因此要提高运算速度, 加法器的速度非常关键。
在进行进位选择加法器讲解之前，先介绍一种选择器，2-1选择器

2-1选择器

2-1选择器是根据一位控制位控制2个输入输出哪一个的电路选择器，电路图如下：

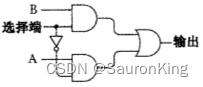
我们可以用C语言实现一下

long select_2_1(long in_1,long in_2,long door)
{
    long a1 =  and_gate(in_1, door);
    long a2 =  and_gate(in_2, not_gate(door));
    return or_gate(a1, a2);
}

并且该C函数可以不止实现单个位的选择，对于64位以内的可以通过该方法返回选择后的值。

进位选择加法器

进位选择加法器是这样一种算法，比如对于64位的加法，分成四部分

• A：0～15位
• B：16～31位
• C：32～47位
• D：48～63位

BCD部分都有两种计算逻辑，一种假设进位为0，一种假设进位为1
所以，A，B0，B1，C0，C1，D0，D1可以并行运算。运算完成后进行拼接，拼接逻辑如下：

• 根据A的进位选择B0或者B1
• 根据上一步选择的B0或者B1是否发生进位选择C0或者C1
• 根据上一步选择的C0或者C1是否发生进位选择D0或者D1

下面看一下C语言的实现

long alu_add_16(long in_1, long in_2)
{
    long ac = 0;
    long bc0 = 0;
    long bc1 = 1;
    long cc0 = 0;
    long cc1 = 1;
    long dc0 = 0;
    long dc1 = 1;
    
    // 下面这些并行运算
    long a = alu_add(in_1, in_2, 16,&ac);
    long b0 = alu_add(in_1>>16, in_2>>16, 16,&bc0);
    long b1 = alu_add(in_1>>16, in_2>>16, 16,&bc1);
    long c0 = alu_add(in_1>>32, in_2>>32, 16,&cc0);
    long c1 = alu_add(in_1>>32, in_2>>32, 16,&cc1);
    long d0 = alu_add(in_1>>48, in_2>>48, 16,&dc0);
    long d1 = alu_add(in_1>>48, in_2>>48, 16,&dc1);
    
    long b = select_2_1(b1, b0, ac);
    long c = select_2_1(c1, c0, b==b1?bc1:bc0);
    long d = select_2_1(d1, d0, c==c1?cc1:cc0);
    return a | b<<16 | c<<32 | d<<48;
}

如何进行减法运算

使用逻辑门进行减法运算，涉及借位，运算比较麻烦，但是我们可以通过操作将减法运算变成加法运算，比如对下面的减法运算：
$$A=X?Y$$
我们可以写成加法的形式：
$$A=X+(?Y)$$

而对于补码编码的数据来说，-Y等于Y取反然后加1，取反操作之需要对Y执行反相器即可，而加1的操作正好可以通过设置加法的初始进位为1来进行处理，下面给出减法运算的C语言电路描述

long alu_not(long in_1, long bits)
{
    long res = 0;
    for(int i = 0;i<bits;i++)
    {
        long x = alu_bit(in_1, i); // 获取输入1的第i位
        res |= (not_gate(x)<<i);
    }
    return res;
}

long alu_sub(long in_1, long in_2, long bits)
{
    long a = alu_not(in_2,64);
	int c = 1;
    return alu_add(in_1, a, bits,&c);
}

这样，我们就使用C语言按照电路图的设计实现了加减的逻辑处理。