算法通关村番外篇-数组实现队列

大家好我是苏麟 , 今天来用数组实现一下队列 .

数组实现队列

顺序存储结构存储的队列称为顺序队列，内部使用一个一维数组存储，用一个队头指针 front 指向队列头部节点(即使用int类型front来表示队头元素的下标)，用一个队尾指针rear(有的地方会用tail，只要在一个问题里统一起来就行了)，指向队列尾部元素(int类型rear来表示队尾节点的下标)。

初始化队列时: front = rear = -1(非必须，也可设置初始值为0，在实现方法时具体修改

队列满时: rear = maxSize - 1 (其中maxSize为初始化队列时，设置的队列最大元素个数)

队列为空时: front = rear

在代码中初始化了一个大小为6的顺序队列

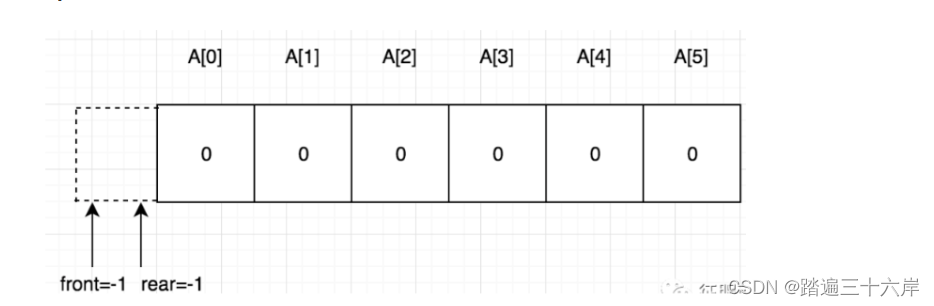
其中 front 和 rear 指向的虚线框实际并不存在，仅用来表示初始化时的默认状态，因为我们实现的队列元素使用int存储元素，所以初始值均为 0(如用Objecl或范型则初始值为null)，执行queue.add(1) 到queue.add(6)方 法后队列的状态如下图:

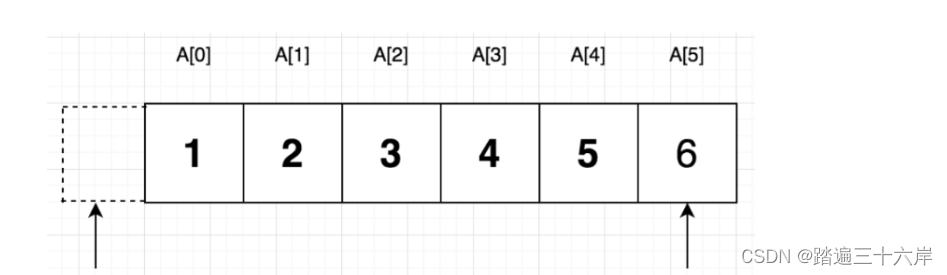
接下来看下队列的出队情况，当第一次执行queue.pop0方法后，队列元素如上图所示，此时队列剩下5个元素:

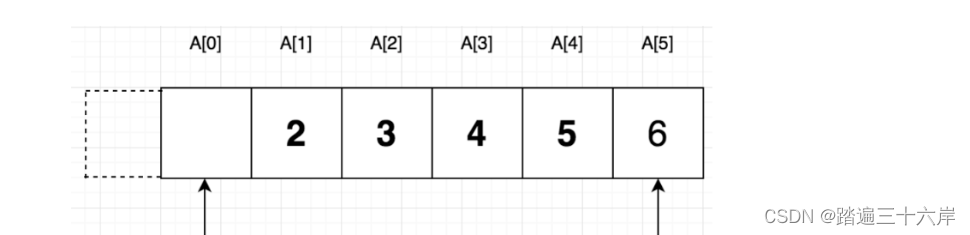
?当第六次执行queue.pop0方法后，队列元素如下图所示 :

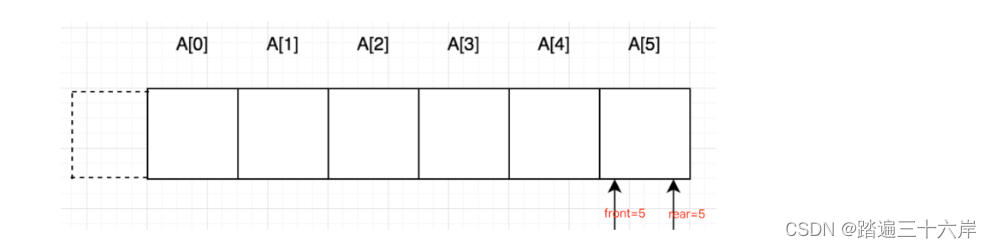
此时队列中元素已全部出队，按正常逻辑应该可以添加元素到队列中，但此时添加元素却会报队列已满错误(rear=maxSize-1)，当然即使前面元素未出队也会报相同错误。这就是我们常说的“假溢出”问题。为解决这个问题，就引出了我们的环形队列。?

代码实现

/**
 * 队列
 */
public class ArrayQueue {
    //队列存放的数据
    private int[] data;
    //队列大小
    private int maxSize;
    //队列头指针
    private int front;
    //队列尾指针
    private int rear;

    public ArrayQueue(int maxSize) {
        data = new int[maxSize];
        this.maxSize = maxSize;
        front = -1;
        rear = -1;
    }

    //判断队列是否满了
    public boolean isFull() {
        return rear == maxSize - 1;
    }

    //判断是否为空
    public boolean isEmpty() {
        return front == rear;
    }

    //添加数据
    public void add(int n) {
        if (isFull()) {
            System.out.println("队列已满!");
            return;
        }
        data[++rear] = n;
    }

    //删除数据
    public int pop() {
        if (isEmpty()) {
            throw new RuntimeException("队列为空 , 请先添加数据!");
        }
        int temp = data[++front];
        data[front] = 0;
        return temp;
    }

    //显示头部数据
    public void head() {
        if (isEmpty()) {
            throw new RuntimeException("队列为空 , 请先添加数据!");
        }
        System.out.println(data[front + 1]);
    }

    //打印全部数据
    public void forEach() {
        if (isEmpty()) {
            System.out.println("队列为空 , 请先添加数据!");
        }
        for (int i = front + 1; i <= rear; i++) {
            System.out.print(data[i] + " ");
        }
    }
}

环形队列

在我们上面基于数组实现的队列中，假如头和尾都到了未尾，虽然这时候个空间是空的，但是无法插入新元素，为此，我们将其设计成环形结构。

环形队列，顾名思义即让普通队列首尾相连，形成一个环形。当 rear 指向尾元素后，当队列有元素出队时可以继续向队列中添加元素。这里使用 rear 指针指向最后一个节点的后一个元素，即会占用一个位置用来表示队列已满。

• 初始化队列时: front = rear = 0
• 队列满时: (rear +1) % maxSize == front(其中maxSize为初始化队列时，设置的队列最大元素
  个数)
• 队列为空时: front == rear。

图解演示 :

入队演示 :

出队 , 入队演示 :?

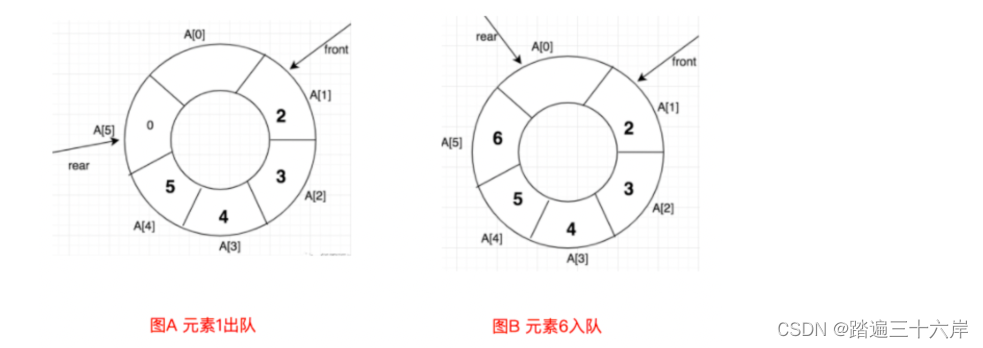
所以这种方式会浪费一个空间来作为判满的条件 .

在这种场景下，环形队列有效元素个数为(rear - front + maxSize) % maxSize 。 (或者在内部定义一个size属性，当元素入队时size++，当出队时size--) 。因此在打印队列中元素时，从 front 位置开始至 front + size 位置结束来循环打印有效元素。

如果不实用环形队列方式实现队列，则会出现“假溢出”情况(即队列满后，将全部元素出队却不能继续添加元素的情况)。而环形队列会在队头元素出队后，将队尾指针rear重新分配为0，以达到循环使用队列空间的目的。

代码 :

/**
 * @className: CycleQueue
 * @author: SL 苏麟
 **/
public class CycleQueue {
    //队列存放的数据
    private int[] data;
    //队列大小
    private int maxSize;
    //队列头指针
    private int front;
    //队列尾指针
    private int rear;

    public CycleQueue(int maxSize) {
        data = new int[maxSize];
        this.maxSize = maxSize;
        front = 0;
        rear = 0;
    }

    //判断队列是否满
    public boolean isFull() {
        return (rear + 1) % maxSize == front;
    }

    //判断是否为空
    public boolean isEmpty() {
        return front == rear;
    }

    //添加元素
    public void add(int n) {
        if (isFull()) {
            System.out.println("Queue is full!!!");
            return;
        }
        data[rear] = n;
        rear = (rear + 1) % maxSize;
    }

    //取出头元素
    public void head() {
        if (isEmpty()) {
            System.out.println("Queue is null!!!");
            return;
        }
        System.out.println("head : " + data[front]);
    }

    //头删
    public int pop() {
        if (isEmpty()) {
            throw new RuntimeException("Queue is null!!!");
        }
        int temp = data[front];
        front = (front + 1) % maxSize;
        return temp;
    }

    //打印队列
    public void printf() {
        if (isEmpty()) {
            throw new RuntimeException("Queue is null!!!");
        }
        for (int i = front; i < front + size(); i++) {
            System.out.print(data[i % maxSize] + " ");
        }
    }

    //返回队列大小
    public int size() {
        return (rear - front + maxSize) % maxSize;
    }
}

这期就到这里 , 下期见!