LeetCode 每日一题 Day 12 (Hard)|| 二维前缀和&二维差分

2132. 用邮票贴满网格图

给你一个m x n的二进制矩阵 grid ，每个格子要么为 0 （空）要么为 1 （被占据）。

给你邮票的尺寸为 stampHeight x stampWidth 。我们想将邮票贴进二进制矩阵中，且满足以下 限制 和 要求 ：

1. 覆盖所有 空 格子。
2. 不覆盖任何 被占据 的格子。
3. 我们可以放入任意数目的邮票。
4. 邮票可以相互有 重叠 部分。
5. 邮票不允许 旋转 。
6. 邮票必须完全在矩阵 内 。

如果在满足上述要求的前提下，可以放入邮票，请返回 true ，否则返回 false 。
示例 1：

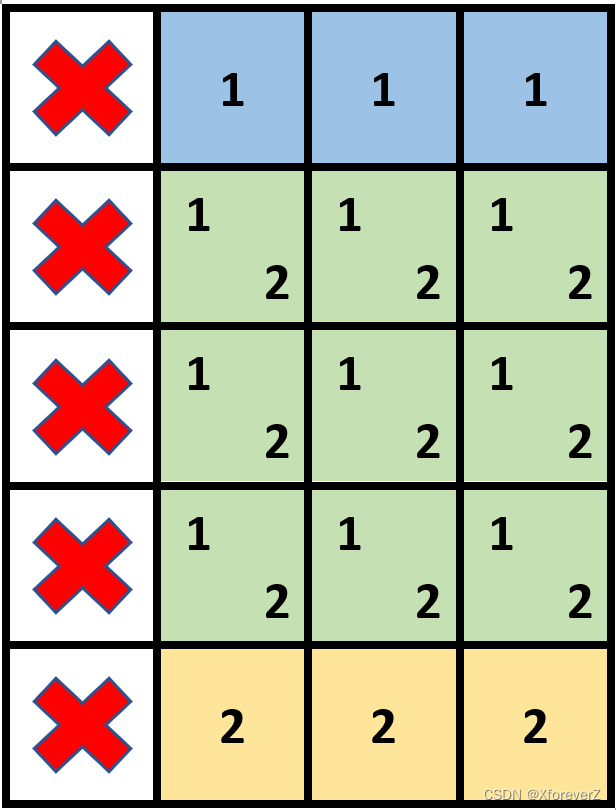
输入：grid = [[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0]], stampHeight = 4, stampWidth = 3
输出：true
解释：我们放入两个有重叠部分的邮票（图中标号为 1 和 2），它们能覆盖所有与空格子。\

示例 2：

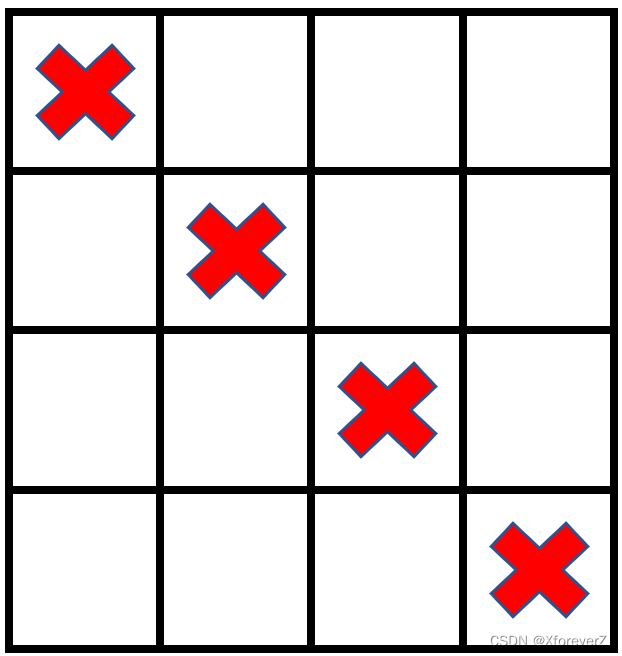
输入：grid = [[1,0,0,0],[0,1,0,0],[0,0,1,0],[0,0,0,1]], stampHeight = 2, stampWidth = 2
输出：false
解释：没办法放入邮票覆盖所有的空格子，且邮票不超出网格图以外。

提示：

m == grid.length
n == grid[r].length
1 <= m, n <= 10⁵
1 <= m * n <= 2 * 10⁵
grid[r][c] 要么是 0 ，要么是 1 。
1 <= stampHeight, stampWidth <= 10⁵

这道题目实在不会做，搬运了灵神的题解:
【算法小课堂】差分数组
一维差分的思想可以推广至二维

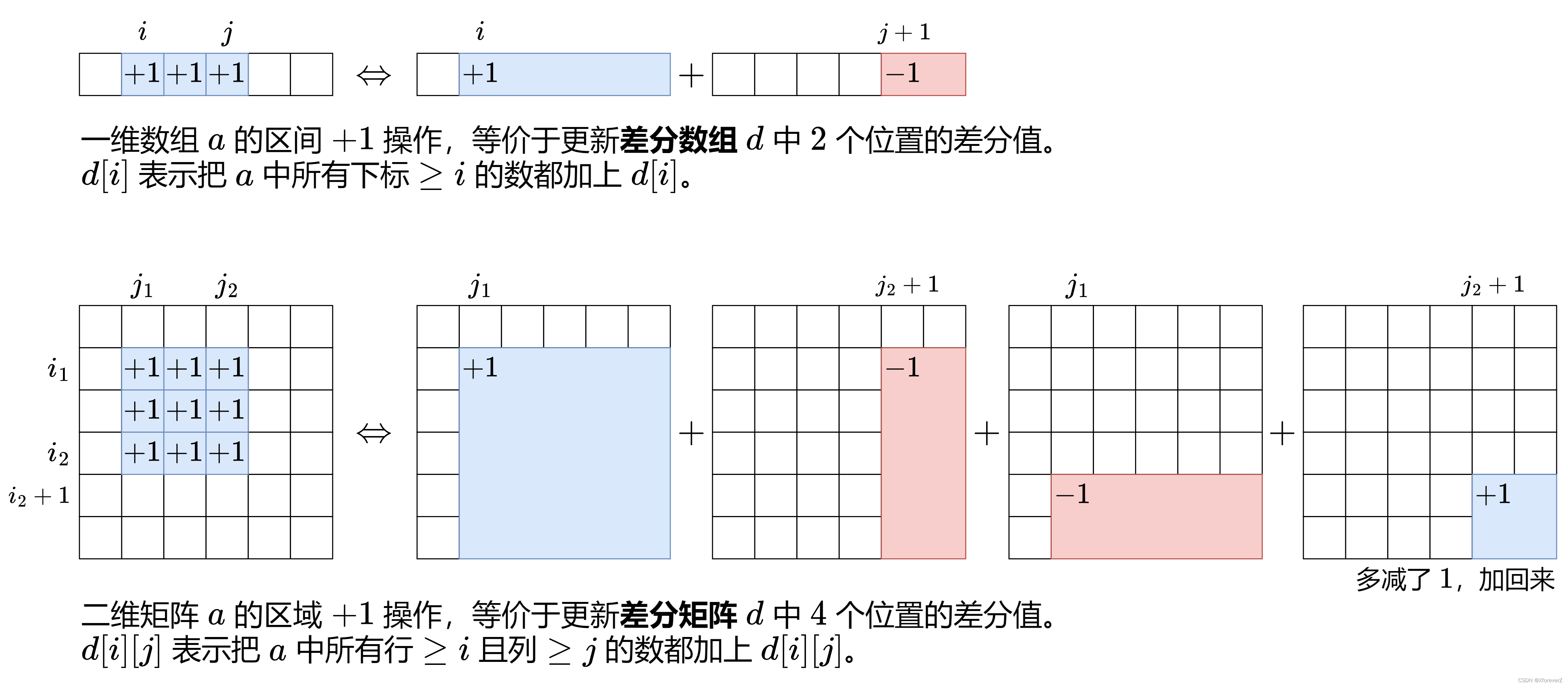
前置知识：二维前缀和
【图解】二维前缀和

思路:

由于邮票可以互相重叠，贪心地想，能放邮票就放邮票。
遍历所有能放邮票的位置去放邮票。注意邮票不能覆盖被占据的格子，也不能出界。
放邮票的同时，记录每个空格子被多少张邮票覆盖。如果存在一个空格子没被邮票覆盖，则返回 false，否则返回 true。
细节
怎么快速判断一个矩形区域可以放邮票？求出 grid 的二维前缀和，从而 O(1) 地求出任意矩形区域的元素和。如果一个矩形区域的元素和等于 0，就表示该矩形区域的所有格子都是 0。
假设用一个二维计数矩阵 cnt记录每个空格子被多少张邮票覆盖，那么放邮票时，就需要把 cnt的一个矩形区域都加一。怎么快速实现？可以用二维差分矩阵 d来代替 cnt。矩形区域都加一的操作，转变成 O(1)地对 d中四个位置的更新操作。
最后从二维差分矩阵 ddd 还原出二维计数矩阵 cnt。类似对一维差分数组求前缀和得到原数组，我们需要对二维差分矩阵求二维前缀和。遍历 cnt，如果存在一个空格子的计数值为 0，就表明该空格子没有被邮票覆盖，返回 false，否则返回 true。代码实现时，可以直接在 d数组上原地计算出 cnt。

来源：灵茶山艾府

class Solution {
public:
    bool possibleToStamp(vector<vector<int>> &grid, int stampHeight, int stampWidth) {
        int m = grid.size(), n = grid[0].size();

        // 1. 计算 grid 的二维前缀和
        vector<vector<int>> s(m + 1, vector<int>(n + 1));
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + grid[i][j];
            }
        }

        // 2. 计算二维差分
        // 为方便第 3 步的计算，在 d 数组的最上面和最左边各加了一行（列），所以下标要 +1
        vector<vector<int>> d(m + 2, vector<int>(n + 2));
        for (int i2 = stampHeight; i2 <= m; i2++) {
            for (int j2 = stampWidth; j2 <= n; j2++) {
                int i1 = i2 - stampHeight + 1;
                int j1 = j2 - stampWidth + 1;
                if (s[i2][j2] - s[i2][j1 - 1] - s[i1 - 1][j2] + s[i1 - 1][j1 - 1] == 0) {
                    d[i1][j1]++;
                    d[i1][j2 + 1]--;
                    d[i2 + 1][j1]--;
                    d[i2 + 1][j2 + 1]++;
                }
            }
        }

        // 3. 还原二维差分矩阵对应的计数矩阵（原地计算）
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                d[i + 1][j + 1] += d[i + 1][j] + d[i][j + 1] - d[i][j];
                if (grid[i][j] == 0 && d[i + 1][j + 1] == 0) {
                    return false;
                }
            }
        }
        return true;
    }
};

灵神的大致思路如下：

1. 计算二维前缀和：

   • 通过二维前缀和矩阵 s，计算每个位置的元素和，用于快速求取任意矩形区域的元素和。通过遍历二维矩阵 grid 实现。

2. 计算二维差分：

   • 通过二维差分矩阵 d，记录每个空格子被邮票覆盖的次数。在这个阶段，通过遍历所有可能放置邮票的位置，判断该位置是否能够放置邮票（即该矩形区域内元素和为零），如果可以，就对差分矩阵 d 进行相应的更新。

3. 还原二维差分矩阵对应的计数矩阵：

   • 对二维差分矩阵 d 进行还原，计算出每个空格子被多少张邮票覆盖。原地计算。

4. 检查是否有未被覆盖的空格子：

   • 最后，遍历原始矩阵 grid，对于每个空格子，如果它是空的（值为 0），并且在计数矩阵中对应位置的计数为零，说明该空格子没有被邮票覆盖，返回 false。如果所有的空格子都被覆盖，返回 true。