动态规划02-不同的二叉搜索树

题目描述

给定一个整数 n，求以 1 … n 为节点组成的二叉搜索树有多少种？

知识预备

什么是二叉搜索树？

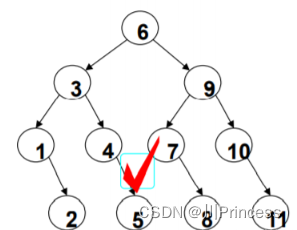
二叉搜索树（BST，Binary Search Tree），也称二叉排序树或二叉查找树。
如果一颗二叉树是二叉搜索树，那么应该满足以下条件：

1. 非空左子树的所有键值小于其根结点的键值。
2. 非空右子树的所有键值大于其根结点的键值。
3. 左、右子树都是二叉搜索树。
   总结而言就是说左<根<右。
   那么对于本题，我们很容易就能看出子里面动态规划的部分是什么，那就是左右子树都是二叉搜索树。

解题思路

根据动态规划解题五部曲

1. 确定dp[i]的含义，这里就假设是从1到i的搜索二叉树数量
2. 首先考虑根节点，由于一共是i个节点，假设当前根节点的数字是j(j<i)，那么根节点左子树的节点数量是j-1，右子树的节点数量是i-j,这里以总结点数为5的为例
   
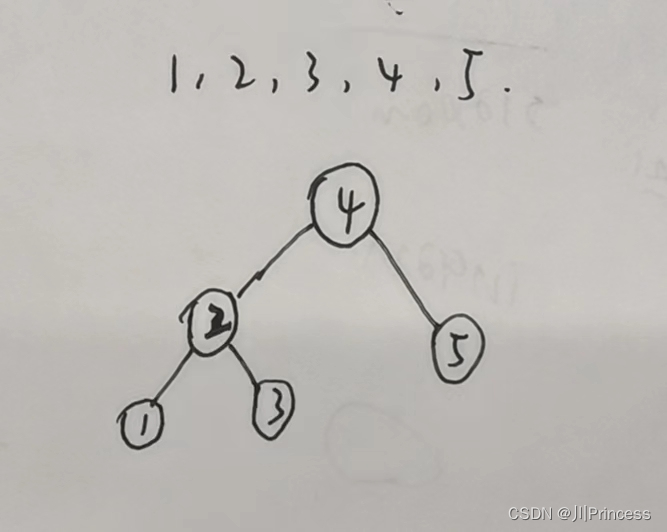
   以当前数字为根节点的二叉搜索树总数就是其左子树可能的数量跟它右子树可能的数量的乘积。同时，总的二叉搜索树数量就是根节点从1一直到i所有dp[i]的总和。
3. dp数组的初始化:因为所有的情况最终都能归结为只有一个节点的情况，然而一个节点又可以由没有节点得出，所以初始化的时候只需要dp[0] = 1即可。
4. 遍历顺序就是从子树开始向父树遍历
5. 验证，带入i = 3,得到一共有5颗二叉搜索树，得证

代码

class Solution {
public:
    int numTrees(int n) {
        vector<int> dp(n + 1);
        dp[0] = 1;//初始化没有数字的搜索二叉树是一颗
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= i; j++) {
                dp[i] += dp[j - 1] * dp[i - j];
            }
        }
        return dp[n];
    }
};