数模学习day10-聚类模型

说明，本文部分图片和内容源于数学建模交流公众号

目录

K-means聚类算法

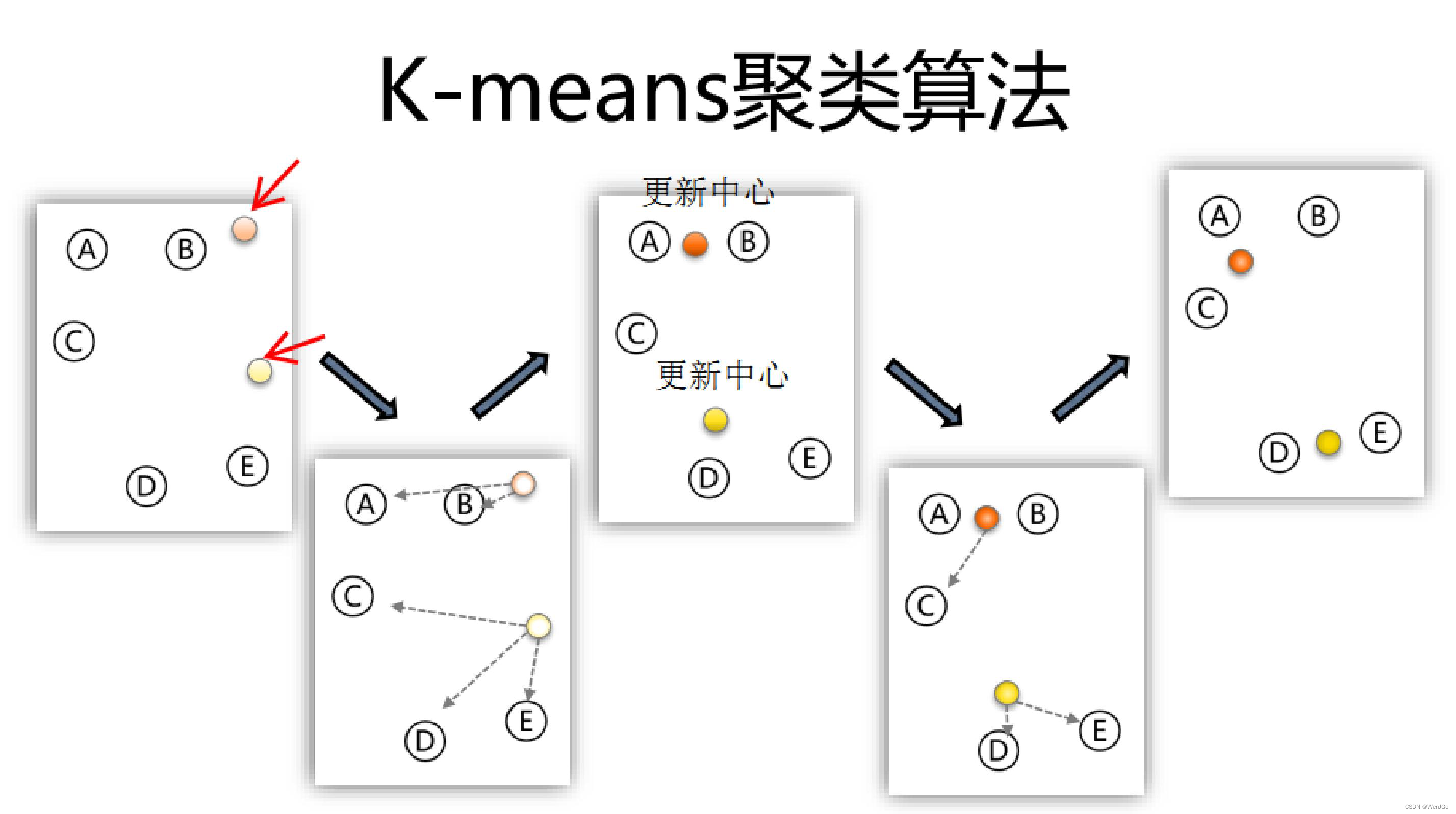
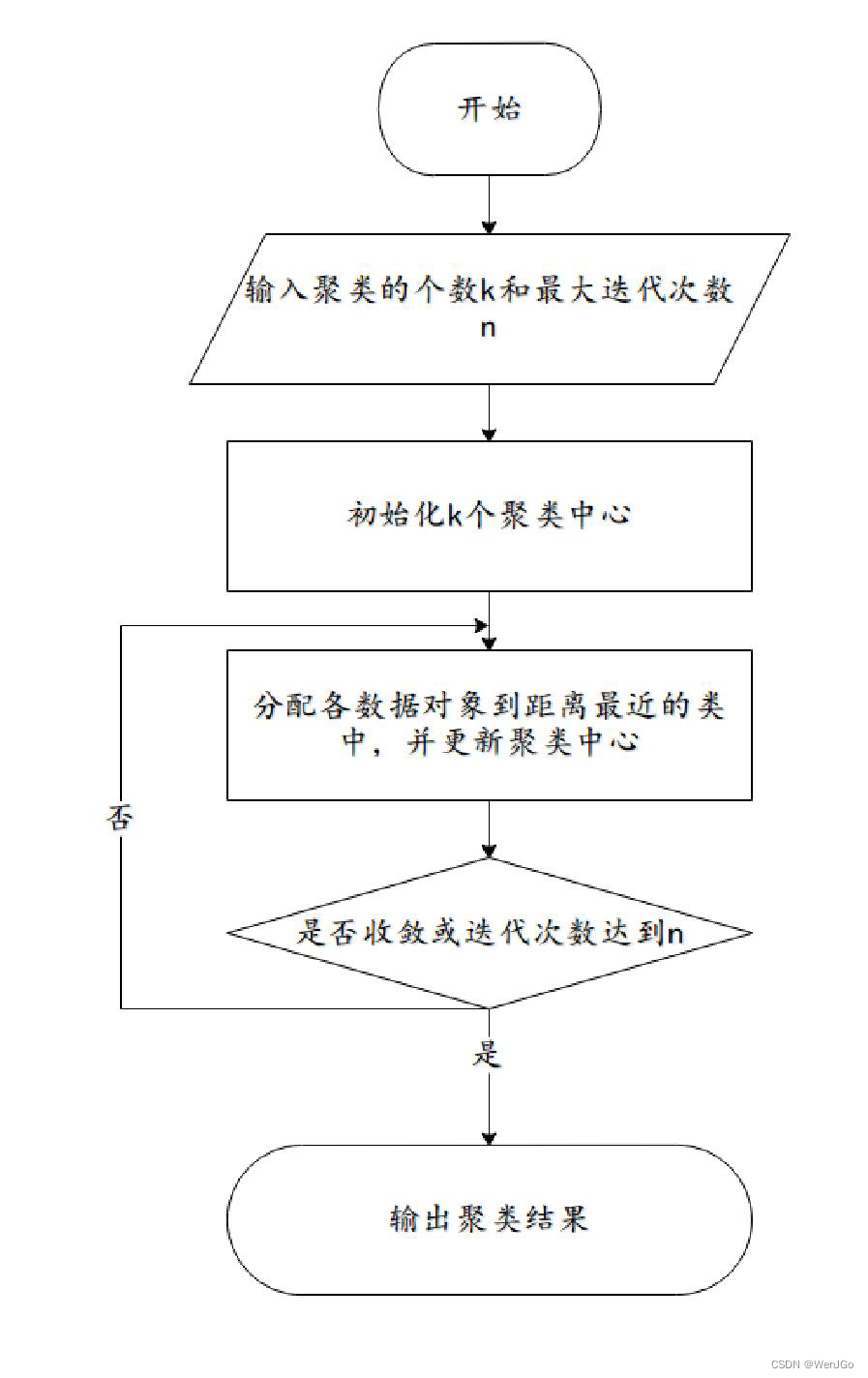
K-means聚类的算法流程：

图解

算法流程图

评价

K-means++算法

基本原则

算法过程

Spss软件操作

K-means算法的疑惑

系统（层次）聚类

算法流程

Spss操作

聚类谱系图（树状图）

用图形估计聚类的数量

小例子

处理数据

聚合系数折线图的画法

确定K后保存聚类结果并画图

示意图

DBSCAN算法

基本概念

Matlab代码

---

K-means聚类算法

K-means聚类的算法流程：

（1）指定需要划分的簇的个数K值（类的个数）
（2）随机地选择K个数据对象作为初始的聚类中心（不一定要是我们的样本点）
（3）计算其余的各个数据对象到这K个初始聚类中心的距离，把数据对象划归到距离它最近的那个中心所处在的簇类中
（4）调整新类并且重新计算出新类的中心
（5）循环步骤三和四，看中心是否收敛（不变），如果收敛或达到迭代次数则停止循环
（6）结束。GG

图解

算法流程图

评价

优点：
（1）算法简单、快速。
（2）对处理大数据集，该算法是相对高效率的。
缺点：
（1）要求用户必须事先给出要生成的簇的数目K。
（2）对初值敏感。
（3）对于孤立点数据敏感。

K-means++算法可解决2和3这两个缺点。

---

K-means++算法

只对K-means算法“初始化K个聚类中心” 这一步进行了优化

基本原则

k-means++算法选择初始聚类中心的基本原则是：

初始的聚类中心之间的相互距离要尽可能的远。

算法过程

（1）随机选取一个样本作为第一个聚类中心；
（2）计算每个样本与当前已有聚类中心的最短距离（即与最近一个聚类中心的距离），这个值越大，表示被选取作为聚类中心的概率较大；最后，用轮盘法（依据概率大小来进行抽选）选出下一个聚类中心；
（3）重复步骤二，直到选出K个聚类中心。选出初始点后，就继续使用标准的K-means算法了。

---

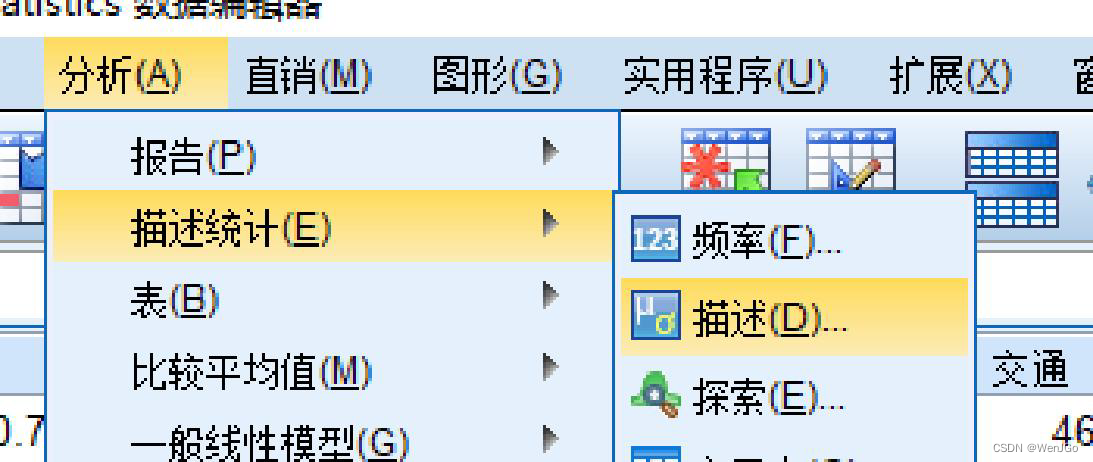
Spss软件操作

这里简略的提到。

---

K-means算法的疑惑

（1）聚类的个数K值怎么定？
答：分几类主要取决于个人的经验与感觉，通常的做法是多尝试几个K值，看分成几类的结果更好解释，更符合分析目的等。
（2）数据的量纲不一致怎么办？
答：如果数据的量纲不一样，那么算距离时就没有意义。例如：如果X1单位是米，X2单位是吨，用距离公式计算就会出现“米的平方”加上“吨的平方”再开平方，最后算出的东西没有数学意义，这就有问题了。

---

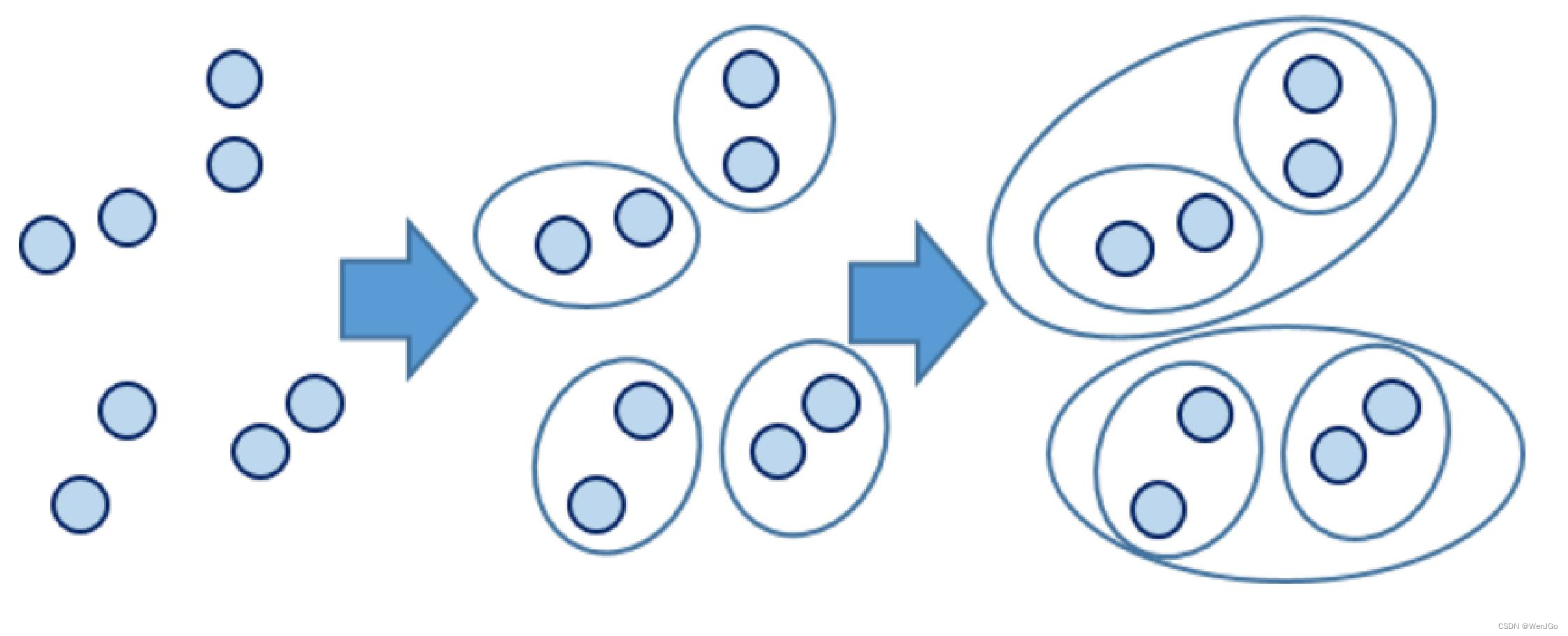
系统（层次）聚类

系统聚类的合并算法通过计算两类数据点间的距离，对最为接近的两类数据点进行组合，并反复迭代这一过程，直到将所有数据点合成一类，并生成聚类谱系图。

算法流程

系统（层次）聚类的算法流程：
（1）将每个对象看作一类，计算两两之间的最小距离；
（2）将距离最小的两个类合并成一个新类；
（3）重新计算新类与所有类之间的距离；
（4）重复二三两步，直到所有类最后合并成一类；
（5）结束。

Spss操作

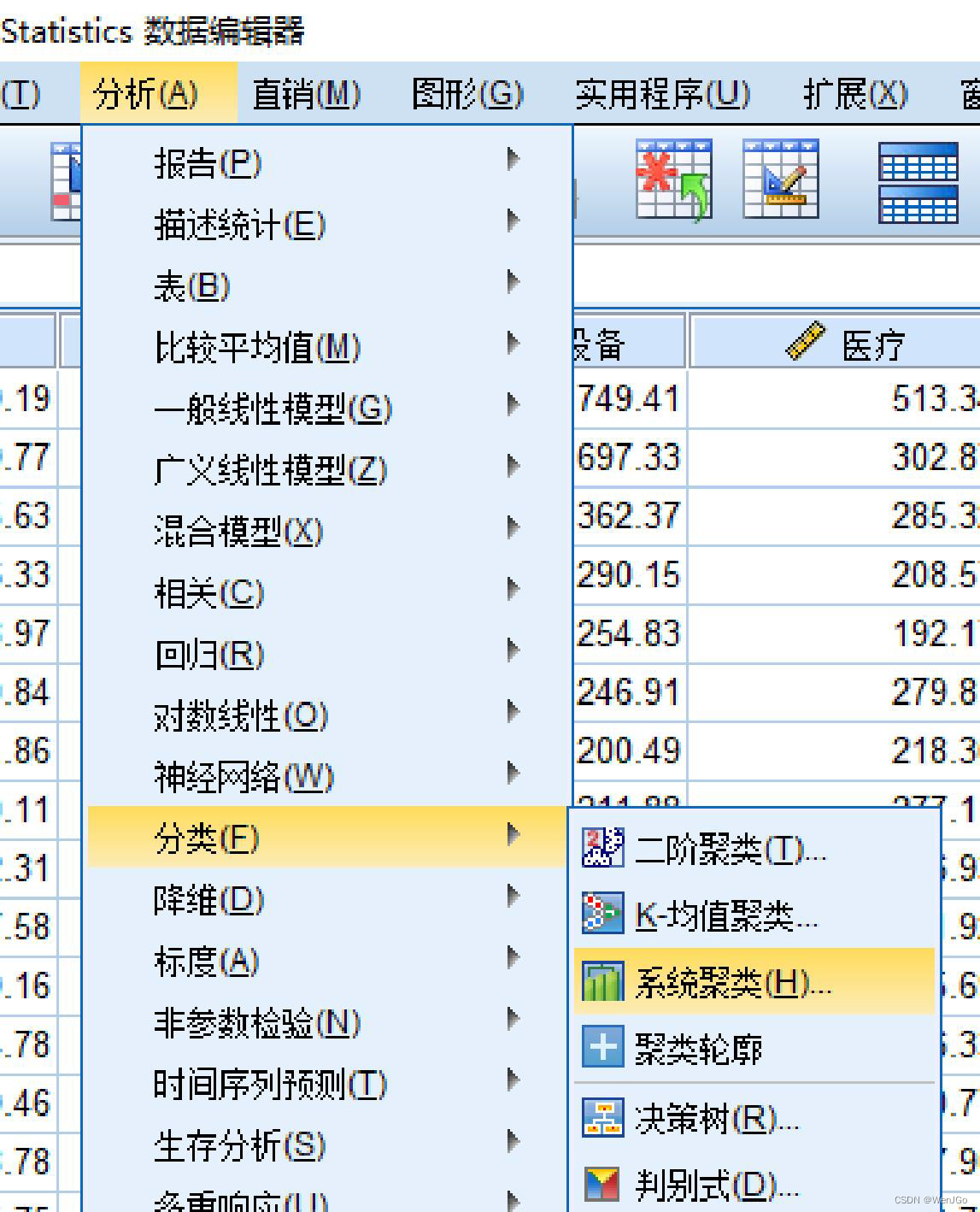
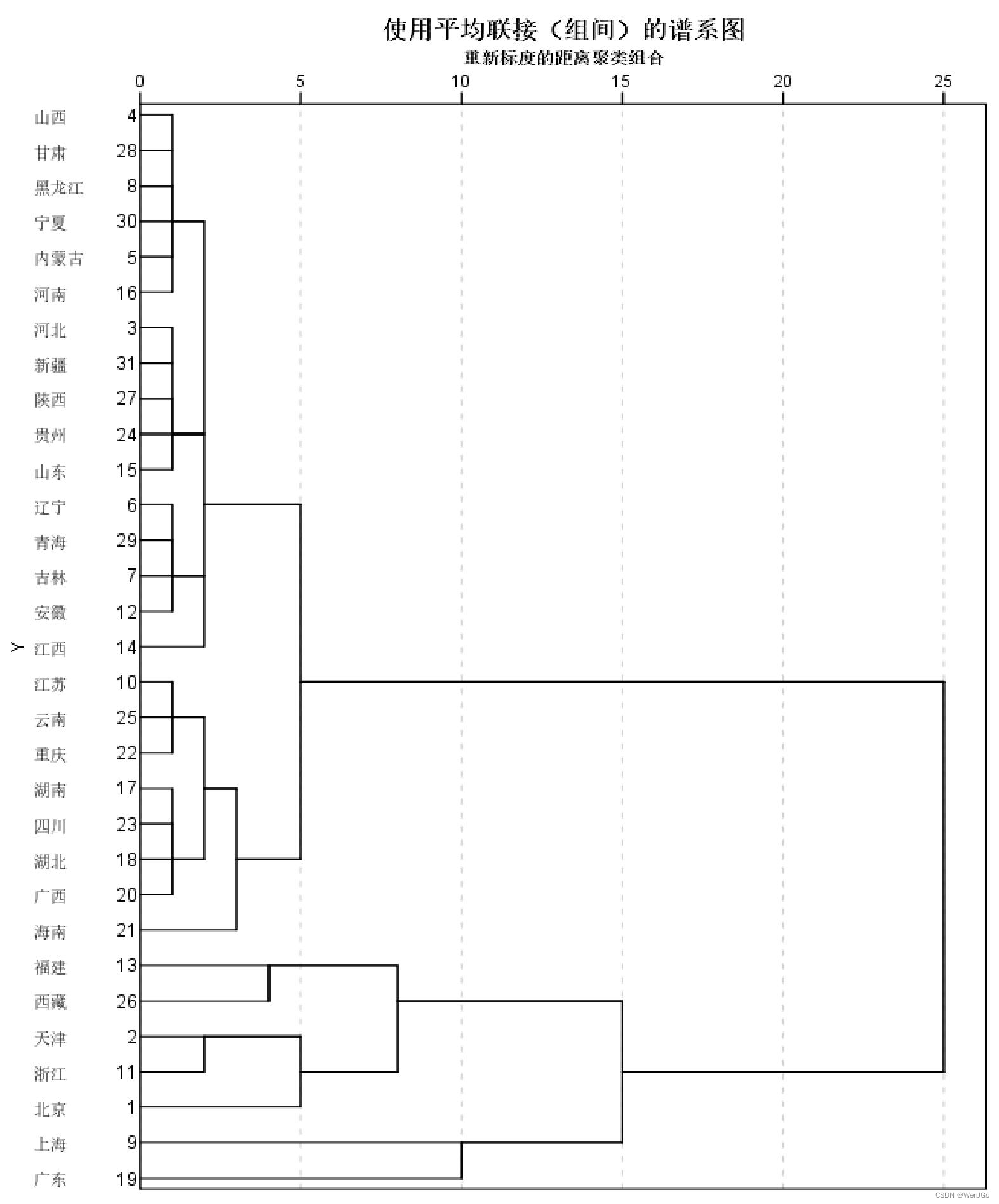
聚类谱系图（树状图）

谱系图是较新的Spss版本添加的功能
横轴表示各类之间的距离
（该距离经过了重新标度）
聚类的个数可以自己从图中决定。
Spss结果中还有一种图，被称为冰柱图，
目前已经很少用了。

用图形估计聚类的数量

肘部法则（Elbow Method）：通过图形大致的估计出最优的聚类数量。

小例子

处理数据

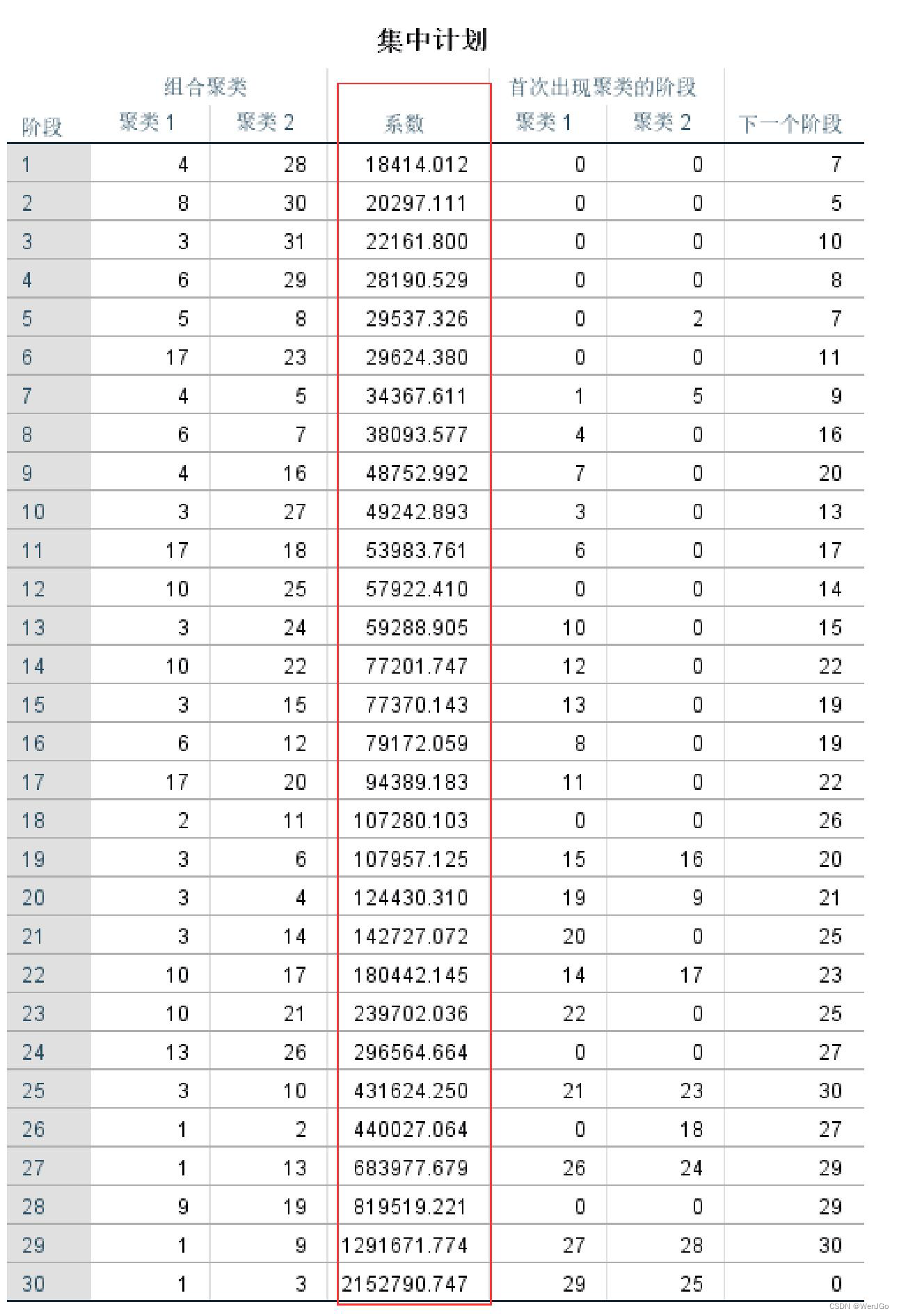
把数据粘贴到Excel表格中，
并按照降序排好。

聚合系数折线图的画法

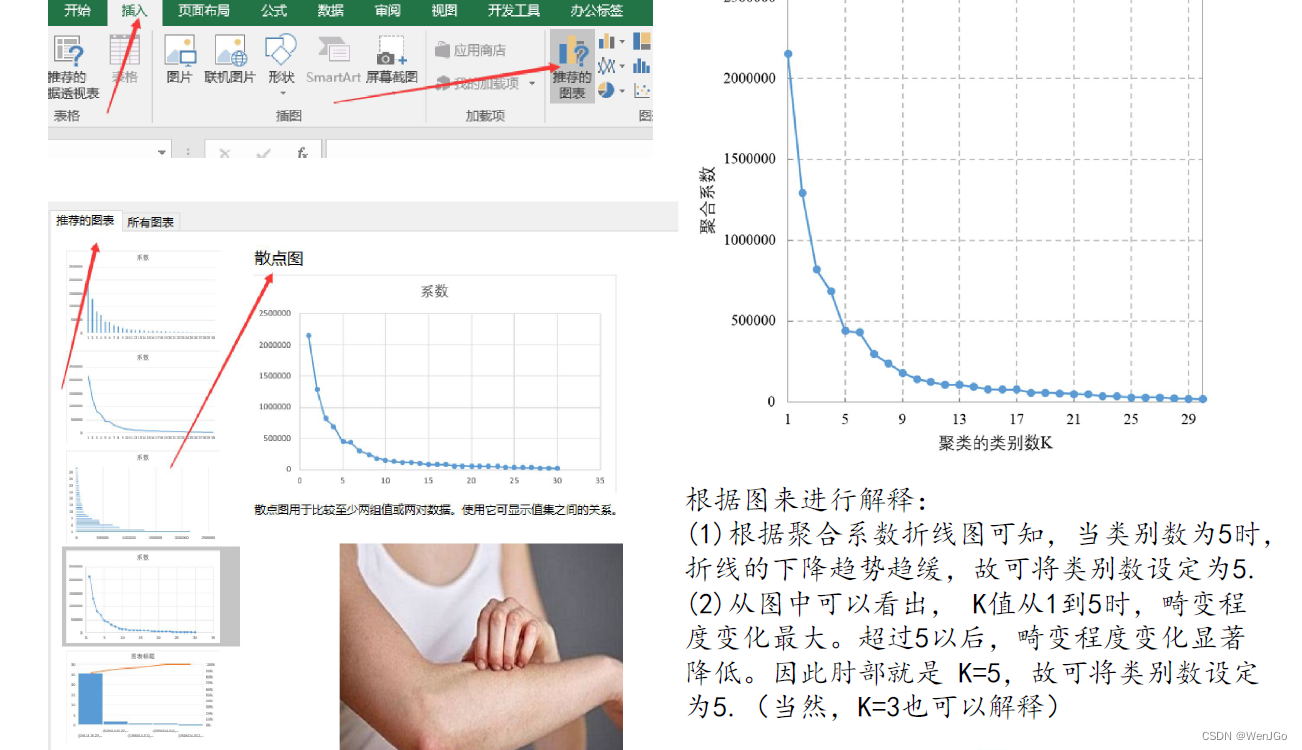
确定K后保存聚类结果并画图

示意图

注意：只要当指标个数为2或者3的时候才能画图，上面两个图纯粹是为了演示作图过程，实际上本例中指标个数有8个，是不可能做出这样的图的。

---

DBSCAN算法

????????DBSCAN(Density-based spatial clustering of applicationswith noise)是Martin Ester, Hans-PeterKriegel等人于1996年提出的一种基于密度的聚类方法，聚类前不需要预先指定聚类的个数，生成的簇的个数不定（和数据有关）。该算法利用基于密度的聚类的概念，即要求聚类空间中的一定区域内所包含对象（点或其他空间对象）的数目不小于某一给定阈值。该方法能在具有噪声的空间数据库中发现任意形状的簇，可将密度足够大的相邻区域连接，能有效处理异常数据。

DBSCAN：具有噪声的基于密度的聚类方法

谁和我挨的近，我就是谁兄弟
兄弟的兄弟，也是我的兄弟

基本概念

DBSCAN算法将数据点分为三类：
? 核心点：在半径Eps内含有不少于MinPts数目的点
? 边界点：在半径Eps内点的数量小于MinPts，但是落在核心点的邻域内
? 噪音点：既不是核心点也不是边界点的点

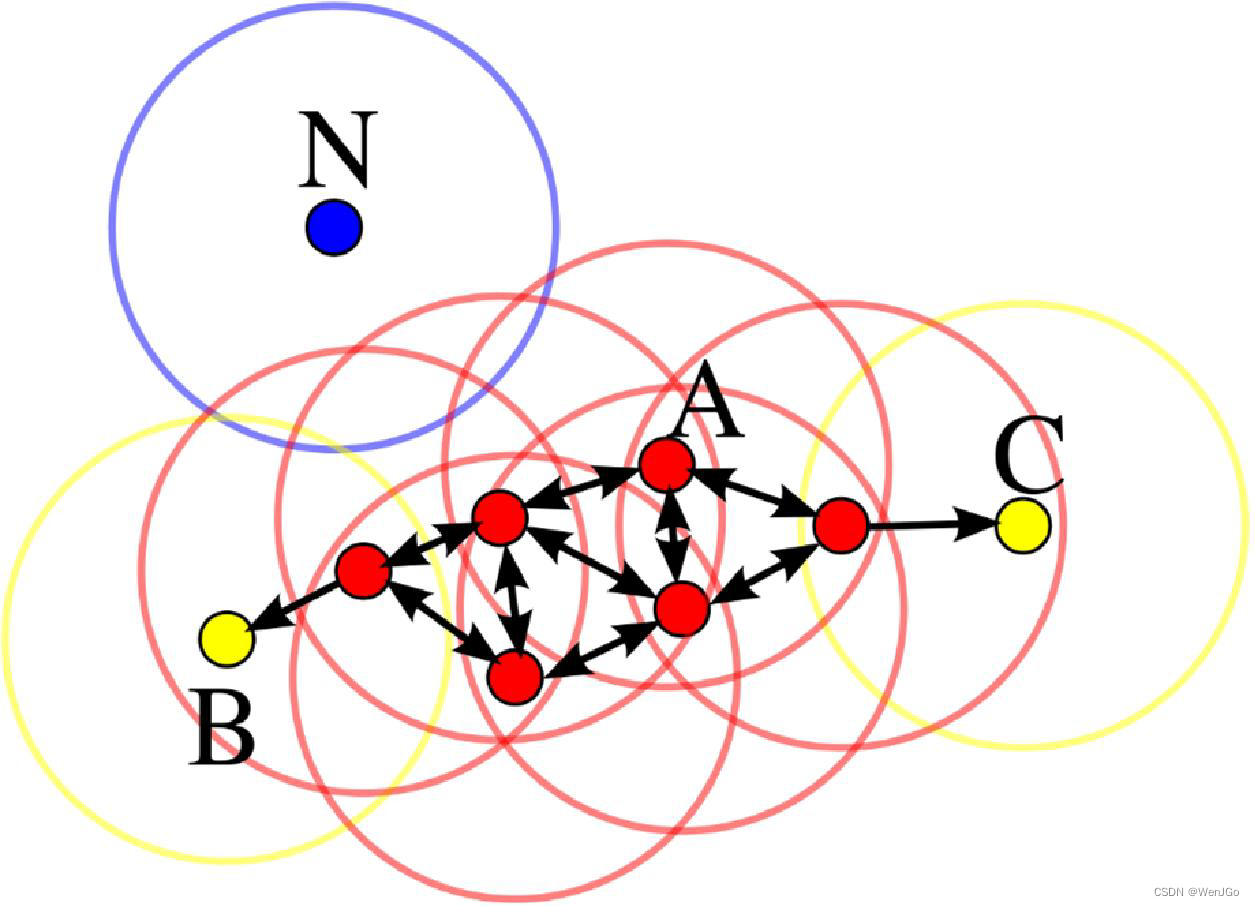
????????在这幅图里，MinPts = 4，点A 和其他红色点是核心点，因为它们的ε-邻域（图中红色
圆圈）里包含最少4 个点（包括自己），由于它们之间相互相可达，它们形成了一个聚类。点B 和点C 不是核心点，但它们可由A 经其他核心点可达，所以也和A属于同一个聚类。点N 是局外点，它既不是核心点，又不由其他点可达。

这个网站可以可视化该算法

可视化 DBSCAN 群集 (naftaliharris.com)

Matlab代码

Matlab官网推荐下载的代码：

DBSCAN Clustering Algorithm - File Exchange - MATLAB Central (mathworks.cn)

注意，MATLAB在2019a版本中正式加入了自己的dbscan函数，内置函数的运行效率
更高，具体使用方法可以查看：

Density-based spatial clustering of applications with noise (DBSCAN) - MATLAB dbscan - MathWorks 中国
也可以看这个推文：

更高效的Dbscan聚类算法 (qq.com)