多变量批量梯度下降python代码

前面几篇分别完成了单变量的处理，其中数据本身范围比较合理以至于损失值没有太离谱。本篇使用的数据集的目标值y和特征X的量级差距过大，因此引入了目标变量的特征归一化处理。
未处理归一化之前的损失：

初始的损失值: 65591548106.45744
下优化后的损失值: 2043280050.607604

处理归一化之后的损失：

初始的损失值: 0.5
下优化后的损失值: 0.13352749098585492

在图片绘制阶段，进行了逆归一化处理。最终绘制图片如下：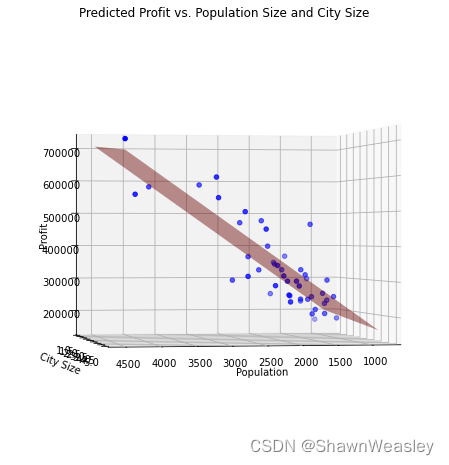
具体代码如下：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import joblib

# 导入数据
path = 'ex1data2.txt'
data = pd.read_csv(path, header=None, names=['Population', 'City Size', 'Profit'])

# 分离特征和目标变量
X = data.iloc[:, 0:2].values  # Population和City Size列
y = data.iloc[:, 2].values    # Profit列

def normalize(array):
    mean = np.mean(array, axis=0)
    std = np.std(array, axis=0)
    normalized_array = (array - mean) / std
    return normalized_array, mean, std

# 使用函数分别归一化特征和目标变量
X_norm, mean_X, std_X = normalize(X)
y_norm, mean_y, std_y = normalize(y)

# 添加截距项
m = len(y)  # 样本数量
X_norm = np.append(np.ones((m, 1)), X_norm, axis=1)

# 初始化模型参数
theta = np.zeros(3)

# 批量梯度下降参数
alpha = 0.01  # 学习率
iterations = 3000  # 迭代次数

# 批量梯度下降算法
def gradientDescent(X, y, theta, alpha, num_iters):
    m = len(y)
    for i in range(num_iters):
        predictions = X.dot(theta)
        errors = np.subtract(predictions, y)
        sum_delta = (alpha / m) * X.transpose().dot(errors)
        theta = theta - sum_delta
    return theta

"""
下降前的损失显示
"""
# 模型评估
def computeCost(X, y, theta):
    predictions = X.dot(theta)
    square_err = (predictions - y) ** 2
    return np.sum(square_err) / (2 * m)
# 计算初始损失
initial_cost = computeCost(X_norm, y_norm, theta)
print("初始的损失值:", initial_cost)

"""
批量梯度下降
"""
# 进行梯度下降以拟合模型
theta = gradientDescent(X_norm, y_norm, theta, alpha, iterations)


"""
下降后的损失显示
"""
# 计算优化后的损失
final_cost = computeCost(X_norm, y_norm, theta)
print("下优化后的损失值:", final_cost)

"""
使用需要预测的数据X进行预测
"""
# 假设的人口和城市大小数据
population_values = [2000, 4000]  # 代表35,000和70,000人口
city_size_values = [2, 3]  # 假设的城市大小值，例如使用平均城市大小

# 对每个人口值进行预测
for pop, city_size in zip(population_values, city_size_values):
    # 首先将原始特征值归一化
    pop_norm = (pop - mean_X[0]) / std_X[0]
    city_size_norm = (city_size - mean_X[1]) / std_X[1]

    # 然后将人口值和城市大小转换为与训练数据相同的格式（包括截距项）
    predict_data = np.array([1, pop_norm, city_size_norm])  # 添加截距项

    # 使用模型进行预测
    predict_profit_norm = np.dot(predict_data, theta)

    # 将预测结果转换回原始尺度
    predict_profit = predict_profit_norm * std_y + mean_y
    print(f"模型预测结果 - 人口: {pop}, 城市大小: {city_size} : {predict_profit}")

"""
使用模型绘制函数
"""
# 创建3D图形
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d', elev=0, azim=80)  # 修改视角

# 使用归一化的特征创建网格
x1_grid, x2_grid = np.meshgrid(np.linspace(X_norm[:, 1].min(), X_norm[:, 1].max(), 100),
                               np.linspace(X_norm[:, 2].min(), X_norm[:, 2].max(), 100))

# 计算对应网格点的预测值（归一化尺度）
f_grid_norm = theta[0] + (theta[1] * x1_grid) + (theta[2] * x2_grid)

# 逆归一化预测值
f_grid = f_grid_norm * std_y + mean_y

# 逆归一化 x 和 y 轴的特征范围（用于绘图）
x1_grid_original = x1_grid * std_X[0] + mean_X[0]
x2_grid_original = x2_grid * std_X[1] + mean_X[1]

# 绘制训练数据点（使用原始尺度）
ax.scatter(data['Population'], data['City Size'], data['Profit'], color='b')

# 绘制预测平面（使用逆归一化的预测值和原始尺度的特征范围）
ax.plot_surface(x1_grid_original, x2_grid_original, f_grid, color='r', alpha=0.5)

# 设置原始尺度的轴标签
ax.set_xlabel('Population')
ax.set_ylabel('City Size')
ax.set_zlabel('Profit')
ax.set_title('Predicted Profit vs. Population Size and City Size')

plt.show()

同样的，最常用的多变量小批量梯度下降代码也放在这里了，将批量梯度下降的算法换成了小批量，效果基本差不多：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import joblib

# 导入数据
path = 'ex1data2.txt'
data = pd.read_csv(path, header=None, names=['Population', 'City Size', 'Profit'])

# 分离特征和目标变量
X = data.iloc[:, 0:2].values  # Population和City Size列
y = data.iloc[:, 2].values    # Profit列

def normalize(array):
    mean = np.mean(array, axis=0)
    std = np.std(array, axis=0)
    normalized_array = (array - mean) / std
    return normalized_array, mean, std

# 使用函数分别归一化特征和目标变量
X_norm, mean_X, std_X = normalize(X)
y_norm, mean_y, std_y = normalize(y)

# 添加截距项
m = len(y)  # 样本数量
X_norm = np.append(np.ones((m, 1)), X_norm, axis=1)

# 初始化模型参数
theta = np.zeros(3)

# 定义批次大小
batch_size = 32  # 例如，32
# 批量梯度下降参数
alpha = 0.01  # 学习率
iterations = 3000  # 迭代次数

# 小批量梯度下降算法
def miniBatchGradientDescent(X, y, theta, alpha, num_iters, batch_size):
    m = len(y)  # 获取样本数量

    for iter in range(num_iters):  # 对于每次迭代
        cost = 0  # 初始化本次迭代的总成本
        indices = np.random.permutation(m)  # 随机打乱样本的索引
        X_shuffled = X[indices]  # 根据打乱的索引重新排列X
        y_shuffled = y[indices]  # 根据打乱的索引重新排列y

        for i in range(0, m, batch_size):  # 将数据分成多个批次进行迭代
            X_i = X_shuffled[i:i+batch_size]  # 获取当前批次的X
            y_i = y_shuffled[i:i+batch_size]  # 获取当前批次的y

            prediction = np.dot(X_i, theta)  # 计算当前批次的预测值
            error = prediction - y_i  # 计算误差

            theta = theta - (alpha / batch_size) * np.dot(X_i.T, error)  # 更新参数
            cost += computeCost(X_i, y_i, theta)  # 计算并累加当前批次的成本

    return theta # 返回最终参数

"""
下降前的损失显示
"""
# 模型评估
def computeCost(X, y, theta):
    predictions = X.dot(theta)
    square_err = (predictions - y) ** 2
    return np.sum(square_err) / (2 * m)
# 计算初始损失
initial_cost = computeCost(X_norm, y_norm, theta)
print("初始的损失值:", initial_cost)

"""
批量梯度下降
"""
# 进行梯度下降以拟合模型
theta = miniBatchGradientDescent(X_norm, y_norm, theta, alpha, iterations, batch_size)


"""
下降后的损失显示
"""
# 计算优化后的损失
final_cost = computeCost(X_norm, y_norm, theta)
print("下优化后的损失值:", final_cost)

"""
使用需要预测的数据X进行预测
"""
# 假设的人口和城市大小数据
population_values = [2000, 4000]  # 代表35,000和70,000人口
city_size_values = [2, 3]  # 假设的城市大小值，例如使用平均城市大小

# 对每个人口值进行预测
for pop, city_size in zip(population_values, city_size_values):
    # 首先将原始特征值归一化
    pop_norm = (pop - mean_X[0]) / std_X[0]
    city_size_norm = (city_size - mean_X[1]) / std_X[1]

    # 然后将人口值和城市大小转换为与训练数据相同的格式（包括截距项）
    predict_data = np.array([1, pop_norm, city_size_norm])  # 添加截距项

    # 使用模型进行预测
    predict_profit_norm = np.dot(predict_data, theta)

    # 将预测结果转换回原始尺度
    predict_profit = predict_profit_norm * std_y + mean_y
    print(f"模型预测结果 - 人口: {pop}, 城市大小: {city_size} : {predict_profit}")

"""
使用模型绘制函数
"""
# 创建3D图形
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d', elev=0, azim=80)  # 修改视角

# 使用归一化的特征创建网格
x1_grid, x2_grid = np.meshgrid(np.linspace(X_norm[:, 1].min(), X_norm[:, 1].max(), 100),
                               np.linspace(X_norm[:, 2].min(), X_norm[:, 2].max(), 100))

# 计算对应网格点的预测值（归一化尺度）
f_grid_norm = theta[0] + (theta[1] * x1_grid) + (theta[2] * x2_grid)

# 逆归一化预测值
f_grid = f_grid_norm * std_y + mean_y

# 逆归一化 x 和 y 轴的特征范围（用于绘图）
x1_grid_original = x1_grid * std_X[0] + mean_X[0]
x2_grid_original = x2_grid * std_X[1] + mean_X[1]

# 绘制训练数据点（使用原始尺度）
ax.scatter(data['Population'], data['City Size'], data['Profit'], color='b')

# 绘制预测平面（使用逆归一化的预测值和原始尺度的特征范围）
ax.plot_surface(x1_grid_original, x2_grid_original, f_grid, color='r', alpha=0.5)

# 设置原始尺度的轴标签
ax.set_xlabel('Population')
ax.set_ylabel('City Size')
ax.set_zlabel('Profit')
ax.set_title('Predicted Profit vs. Population Size and City Size')

plt.show()

注：本文为学习吴恩达版本机器学习教程的代码整理，使用的数据集为https://github.com/fengdu78/Coursera-ML-AndrewNg-Notes/blob/f2757f85b99a2b800f4c2e3e9ea967d9e17dfbd8/code/ex1-linear%20regression/ex1data2.txt