机器学习（四） -- 模型评估（1）

系列文章目录

机器学习（一） -- 概述

机器学习（二） -- 数据预处理（1-3）

机器学习（三） -- 特征工程（1-2）

机器学习（四） -- 模型评估（1-4）

未完待续……

---

目录

系列文章目录

前言

一、模型评估概述

1、模型评估定义

2、基本概念

3、过拟合、欠拟合

3.1、过拟合

3.2、欠拟合

3.3、防止欠拟合，过拟合的方法

4、偏差、方差

4.1、偏差（biase）

4.2、方差（variance）

4.3、噪声（Noise）

二、评估方法

1、留出法

2、交叉验证法（k折交叉验证）

3、留一法

4、自助法

---

机器学习（四） -- 模型评估（2）

机器学习（四） -- 模型评估（3）

---

前言

tips：这里只是总结，不是教程哈。

“***”开头的是给好奇心重的宝宝看的，其实不太重要可以跳过。

此处以下所有内容均为暂定，因为我还没找到一个好的，让小白（我自己）也能容易理解（更系统、嗯应该是宏观）的讲解顺序与方式。

第一文主要简述了一下机器学习大致有哪些东西（当然远远不止这些），对大体框架有了一定了解。接着我们根据机器学习的流程一步步来学习吧，掐掉其他不太用得上我们的步骤，精练起来就4步（数据预处理，特征工程，训练模型，模型评估），其中训练模型则是我们的重头戏，基本上所有算法也都是这一步，so，这个最后写，先把其他三个讲了，然后，在结合这三步来进行算法的学习，兴许会好点（个人拙见）。

---

一、模型评估概述

1、模型评估定义

对训练好的模型性能进行评估。

2、基本概念

错误率（error rate）：分类错误的样本数/样本总数

精度（accuracy）：1-错误率=分类正确的样本数/样本总数

误差（error）：学习器（模型）的预测输出与样本真实输出的差异。（误差期望，排除数据集大小的影响）

????????训练误差（training error，经验误差，empirical error）：学习器在训练集上的误差。

?????????测试误差（test error）：学习器在测试集上的误差。

?????????泛化误差（generalization error）：学习器在未知新样本上的误差。（我们是为了得到泛化误差小的学习器。因为，泛化误差无法测量，因此，通常我们会将测试误差近似等同于泛化误差。）

3、过拟合、欠拟合

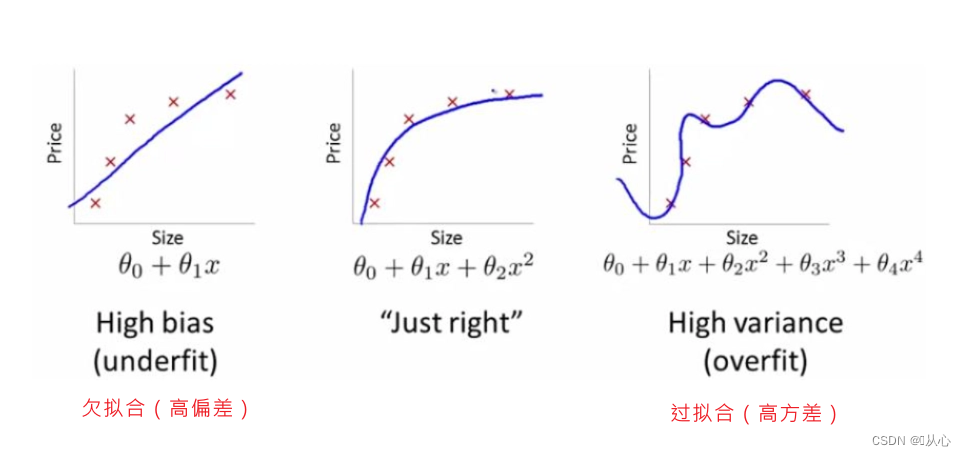
3.1、过拟合

模型对于训练数据拟合得太好了。
很可能已经把训练样本自身的一些特点当作所有潜在样本都会具有的一般性质，这样就会导致泛化性能下降。反映到评估指标上，就是模型在训练集上的表现很好，但在测试集和新数据上的表现较差。

（过拟合是机器学习的关键障碍，虽然各类学习算法都必然带有一些针对过拟合的措施；然而，必须认识到过拟合是无法彻底避免的，我们所能做的只是“缓解”，或者说减小其风险。）

3.2、欠拟合

指模型在训练数据上拟合得不好。
反映到评估指标上，是模型在训练和预测时表现都不好的情况。主要原因在于模型的学习能力低下。

3.3、防止欠拟合，过拟合的方法

3.3.1、防止欠拟合

数据：

????????获得更多的训练数据：更多的样本能够让模型学习到更多更有效的特征，减小噪声的影响。

????????添加新特征：当特征不足或者现有特征与样本标签的相关性不强时，模型容易出现欠拟合。

????????????????挖掘“上下文特征”、“ID 类特征”、“组合特征”等新的特征。

????????????????深度学习：因子分解机、梯度提升决策树、Deep-crossing 等都可以成为丰富特征的方法。

模型：

????????增加模型复杂度：通过增加模型的复杂度可以使模型拥有更强的拟合能力。

????????????????线性模型：添加高次项。

????????????????决策树模型：不采用剪枝手段，不限制叶节点的个数以及树的深度。

????????????????神经网络：增加网络层数或神经元个数。

????????减小正则化系数：针对性地减小正则化系数。（后面会说到）

3.3.2、防止过拟合

数据：

????????获得更多的训练数据：更多的样本能够让模型学习到更多更有效的特征，减小噪声的影响。

????????????????图像分类问题：通过图像的平移、旋转、缩放等方式扩充数据。
????????????????生成式对抗网络：合成大量的新训练数据。

模型：

????????降低模型复杂度：在数据较少时，模型过于复杂是产生过拟合的主要因素，适当降低模型复杂度可以避免模型拟合过多的采样噪声。
????????????????神经网络：减少网络层数、神经元个数。
????????????????决策树：降低树的深度和叶节点的个数、进行剪枝等。
????????正则化方法：给模型的参数加上一定的正则约束，比如将权值的大小加入到损失函数中。常用的惩罚项有 L1 惩罚项和 L2 惩罚项。
????????集成学习方法：把多个模型集成在一起，来降低单一模型的过拟合风险。

4、偏差、方差

模型泛化能力：指机器学习算法对未知样本的适应能力。?

通常我们会用过拟合、欠拟合来定性地描述模型是否很好地解决了特定的问题。
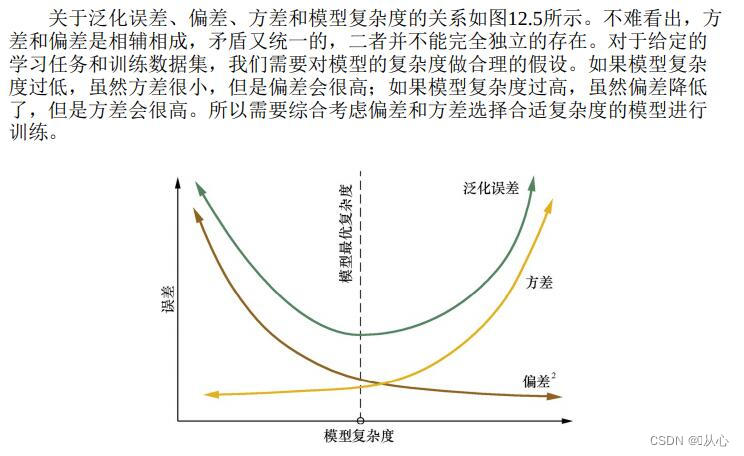
从定量的角度来说，可以用模型的偏差（Bias）与方差（Variance）来描述模型的泛化性能，这称为偏差-方差分解（bias-variance decomposition），是解释学习算法泛化性能（即为什么具有这样的性能）的一种重要工具。

这个训练数据集的损失与一般化的数据集的损失之间的差异就叫做泛化误差（generalization error）。而泛化误差可以分解为偏差（Biase）、方差（Variance）和噪声（Noise）。

4.1、偏差（biase）

是用所有可能的训练数据集训练出的所有模型的输出的平均值与真实模型的输出值之间的差异。

4.2、方差（variance）

是不同的训练数据集训练出的模型输出值之间的差异。即刻画了数据扰动所造成的影响。（预测值离散程度）

4.3、噪声（Noise）

噪声的存在是学习算法所无法解决的问题，数据的质量决定了学习的上限。假设在数据已经给定的情况下，此时上限已定，我们要做的就是尽可能的接近这个上限。

为了更好地说明偏差与方差的关系，以射击靶心作为例子。

二、评估方法

因为通常通过实验测试来对学习器的泛化误差进行评估并进而做出选择。而上面也说过因为泛化误差无法测量，因此，通常我们会将测试误差近似等同于泛化误差。所以需要将数据集进行划分。

1、留出法

留出法将测试数据集和训练数据集完全分开，采用测试数据集来评估算法模型。

其实就是和数据划分讲的一样。一般训练集S占70%-80%，测试集T占20%-30%。（数据量越大，训练集占比越大）
训练集用于训练算法生成模型。测试集通过模型来预测结果并与已知结果比较，最终通过一些模型评价指标评估算法模型的优劣。

训练集和测试集的划分要尽可能保持数据分布的一致性，避免因数据划分过程引入额外的偏差而对最终结果产生影响。基于该情况考虑的采样方式称为“分层采样”。

API：

sklearn.model_selection.train_test_split
导入：
from sklearn.model_selection import train_test_split

eg：

from sklearn.model_selection import train_test_split

# 先查看原先数据集的尺寸
print(iris.data.shape)  # 输出 (150, 4)


# 按照 70%训练集 30% 测试集进行划分
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.3, random_state=134)
print(x_train.shape)  # 输出训练集尺寸(105, 4)
print(x_test.shape)  # 输出测试集尺寸(45, 4)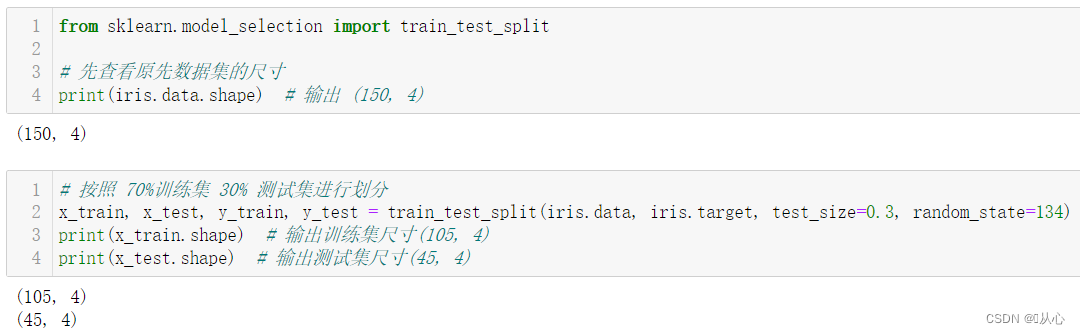

2、交叉验证法（k折交叉验证）

交叉验证法（cross validation）先将数据集 D 划分为 k 个大小相似的互斥子集，每次用k-1个子集的并集做训练集，余下那个做测试集，最终k次训练和测试，最终返回的是k个测试结果的均值。

?

?【当不知道如何选择分离数据集的方法时，请选择 K 折交叉验证来分离数据集；】
【当不知道如何设定 K 值时，请将 K 值设为 10。】

API:

sklearn.model_selection.cross_val_score
导入
from sklearn.model_selection import cross_val_score

实例：

from sklearn.model_selection import cross_val_score
from sklearn.tree import DecisionTreeClassifier

score = cross_val_score(DecisionTreeClassifier(), iris.data, iris.target, cv=10)
print("%.3f%% (%.3f)" % (score.mean() * 100, score.std() * 100)) 
print(score)

3、留一法

留一法（Leave-One-Out，简称 LOO），假定数据集 D 中包含 m 个样本，若令 k = m，则得到交叉验证法的一个特例，即留一法，又被称为“弃一交叉验证”。

k=m，每个样本就是一个子集。

缺点：数据量较大时对算力要求较高

实例：

from sklearn.model_selection import LeaveOneOut
from sklearn.model_selection import cross_val_score
from sklearn.tree import DecisionTreeClassifier

loo = LeaveOneOut()
score = cross_val_score(DecisionTreeClassifier(), iris.data, iris.target, cv=loo)
print("%.3f%% (%.3f)" % (score.mean() * 100, score.std() * 100))  
print(score)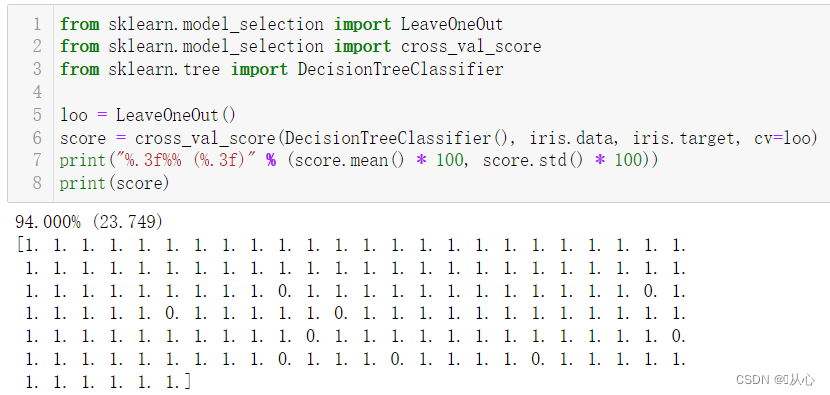

?

4、自助法

自助法（bootstraping）直接以自助采样法（bootstrap sampling）为基础。

D为基础，随机抽取放回抽样m次，产生D'，
m次采样中始终不被采到的概率是（1-1/m）^m，取极限得到0.368
D'做训练集，D\D'（D-D'）做测试集，即有36.8%做测试集

也可以如下描述：给定包含 m 个样本的数据集 D，对其进行采样产生数据集 D’：

每次随机从 D 中挑选一个样本，将其拷贝放入 D’；
然后再将该样本放回初始数据集 D 中，使得该样本在下次采样时仍有可能被采到，其实就是有放回地采样；
该过程重复执行 m 次后，就得到包含 m 个样本的数据集 D’。

这样的测试结果称为“包外估计”。

适用于：数据集较小，难以划分的时候。

缺点：改变初始数据集分布，会引入估计偏差