代码随想录刷题题Day16

2023-12-18 12:47:56

刷题的第十六天，希望自己能够不断坚持下去，迎来蜕变。😀😀😀
刷题语言：C++
Day16 任务
● 654.最大二叉树
● 617.合并二叉树
● 700.二叉搜索树中的搜索
● 98.验证二叉搜索树

1 最大二叉树

构造树一般采用前序遍历，因为先构造中间节点，然后递归构造左子树和右子树

（1）确定递归函数的参数和返回值
参数：存放元素的数组
返回值：指向节点的指针

TreeNode* construct(vector<int>& nums)

（2）确定终止条件

输入的数组大小一定是大于等于1的，所以我们不用考虑小于1的情况，那么当递归遍历的时候，如果传入的数组大小为1，说明遍历到了叶子节点

TreeNode* node = new TreeNode(0);
if (nums.size() == 1) {
	node->val = nums[0];
	return node;
}

（3）确定单层递归的逻辑：中、左、右

先找到数组中最大的值和对应的下标，最大的值构造根节点，下标用来下一步分割数组

int maxValue = 0;
int index = 0;
for (int i = 0; i < nums.size(); i++) {
	if (nums[i] > maxValue) {
		maxValue = nums[i];
		index = i;
	}
}
TreeNode* node = new TreeNode(maxValue);

最大值所在的下标左区间构造左子树

要判断index > 0，因为要保证左区间至少有一个数值

if (index > 0) {
	vector<int> vec(nums.begin(), nums.begin() + index);
	node->left = construct(vec);
}

最大值所在的下标右区间构造右子树

判断index < (nums.size() - 1)，确保右区间至少有一个数值

if (index < nums.size() - 1) {
	vector<int> vec(nums.begin() + index + 1, nums.end());
	node->right = construct(vec);
}

C++：

class Solution {
public:
    TreeNode* construct(vector<int>& nums) {
        if (nums.size() == 1) return new TreeNode(nums[0]);
        // 找到数组中最大的值和对应的下标
        int maxValue = 0;
        int index = 0;
        for (int i = 0; i < nums.size(); i++) {
            if (maxValue < nums[i]) {
                maxValue = nums[i];
                index = i;
            }
        }
        TreeNode* node = new TreeNode(maxValue);
        // 最大值所在的下标左区间 构造左子树
        if (index > 0) {
            vector<int> vec(nums.begin(), nums.begin() + index);
            node->left = construct(vec);
        }
        // 最大值所在的下标右区间 构造右子树
        if (index < nums.size() - 1) {
            vector<int> vec(nums.begin() + index + 1, nums.end());
            node->right = construct(vec);
        }
        return node;
        
    }
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        return construct(nums);
    }
};

以上代码比较冗余，效率也不高，每次还要切割的时候每次都要定义新的vector。
优化：每次分隔不用定义新的数组，而是通过下标索引直接在原数组上操作
优化代码：

class Solution {
public:
	// 在左闭右开区间[left, right)，构造二叉树
    TreeNode* traversal(vector<int>& nums, int left, int right) {
        if (left >= right) return NULL;
        int index = left;
        for (int i = left + 1; i < right; i++) {
            if (nums[i] > nums[index]) index = i;
        } 
        TreeNode* root = new TreeNode(nums[index]);
        // 左闭右开：[left, maxValueIndex)
        root->left = traversal(nums, left, index);
        // 左闭右开：[maxValueIndex + 1, right)
        root->right = traversal(nums, index + 1, right);
        return root;
    }
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        return traversal(nums, 0, nums.size());
    }
};

类似用数组构造二叉树的题目，每次分隔尽量不要定义新的数组，而是通过下标索引直接在原数组上操作，这样可以节约时间和空间上的开销。

一般情况来说：如果让空节点（空指针）进入递归，就不加if，如果不让空节点进入递归，就加if限制一下，终止条件也会相应的调整。

2 合并二叉树

617.合并二叉树
在这里插入图片描述
思路：
递归法

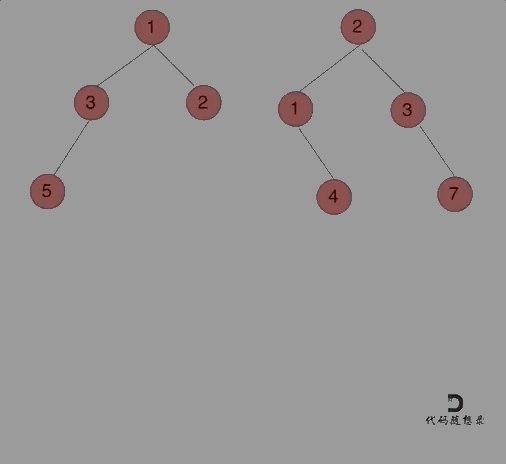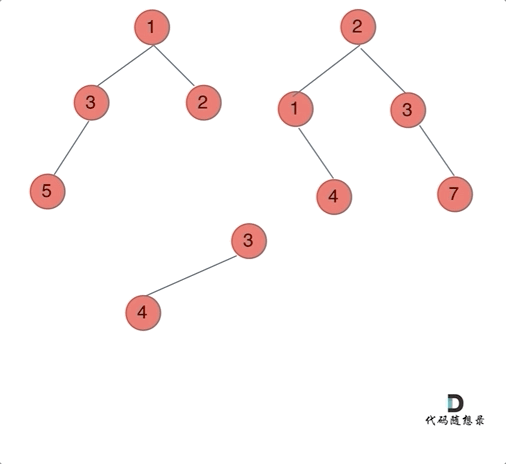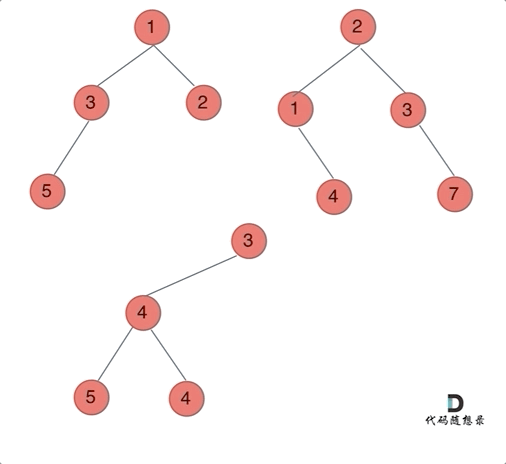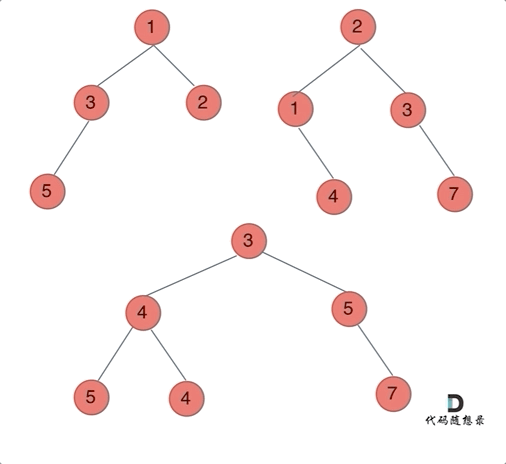
（1）确定递归函数的参数和返回值
参数：两个二叉树的根节点
返回值：合并之后二叉树的根节点

TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2)

（2）确定终止条件
传入了两个树，那么就有两个树遍历的节点t1 和 t2

如果t1 == NULL 了，两个树合并就应该是 t2
反过来如果t2 == NULL，那么两个数合并就是t1

if (root1 == NULL) return root2;
if (root2 == NULL) return root1;

（3）确定单层递归的逻辑
不构造新的二叉树：

root1->val += root2->val;
root1->left = mergeTrees(root1->left, root2->left);
root1->right = mergeTrees(root1->right, root2->right);
return root1;

构造新的二叉树：

TreeNode* root = new TreeNode(0);
root->val = root1->val + root2->val;
root->left = mergeTrees(root1->left, root2->left);
root->right = mergeTrees(root1->right, root2->right);
return root;

C++：

class Solution {
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        if (root1 == NULL) return root2;// 如果t1为空，合并之后就应该是t2
        if (root2 == NULL) return root1; // 如果t2为空，合并之后就应该是t1
        root1->val += root2->val;// 中
        root1->left = mergeTrees(root1->left, root2->left);// 左
        root1->right = mergeTrees(root1->right, root2->right);// 右
        return root1;
    }
};

3 二叉搜索树中的搜索

700.二叉搜索树中的搜索
在这里插入图片描述
思路：

二叉搜索树的特性：
（1）若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
（2）若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
（3）左、右子树也分别为二叉搜索树

递归法
（1）确定递归函数的参数和返回值

TreeNode* searchBST(TreeNode* root, int val)

（2）确定终止条件

如果root为空，或者找到这个数值了，就返回root节点

if (root == NULL || root->val == val) return root;

（3）确定单层递归的逻辑
二叉搜索树的节点是有序的，所以可以有方向的去搜索

如果root->val > val，搜索左子树，如果root->val < val，就搜索右子树，最后如果都没有搜索到，就返回NULL

TreeNode* result = NULL;
if (root->val > val) result = searchBST(root->left, val);
if (root->val < val) result = searchBST(root->right, val);
return result;

C++：

class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        if (root == NULL || root->val == val) return root;
        TreeNode* result = NULL;
        if (root->val > val) {
            result = searchBST(root->left, val);
        }
        if (root->val < val) {
            result = searchBST(root->right, val);
        }
        return result;
    }
};

迭代法
因为二叉搜索树的特殊性，可以不使用辅助栈或者队列就可以写出迭代法

对于一般二叉树，递归过程中还有回溯的过程，例如走一个左方向的分支走到头了，那么要调头，在走右分支
对于二叉搜索树，不需要回溯的过程，因为节点的有序性就帮我们确定了搜索的方向

C++：

class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        while (root != NULL) {
            if (root->val > val) {
                root = root->left;
            }
            else if (root->val < val) {
                root = root->right;
            }
            else return root;
        }
        return NULL;
    }
};

总结：

针对二叉搜索树的题目，一定要利用其特性

4 验证二叉搜索树

98.验证二叉搜索树
在这里插入图片描述
思路：
中序遍历，输出的二叉搜索树节点的数值是有序序列
验证二叉搜索树：判断一个序列是不是递增

递归法
递归中序遍历将二叉搜索树转变成一个数组

vector<int> vec;
void traversal(TreeNode* root) {
	if (root == NULL) return;
	traversal(root->left);
	vec.push_back(root->val);// 将二叉搜索树转换为有序数组
	traversal(root->right);
}

比较一下这个数组是否有序，二叉搜索树中不能有重复元素

traversal(root);
for (int i = 1; i < vec.size(); i++) {
	if (vec[i] <= vec[i - 1]) return false;
}
return true;

C++：

class Solution {
public:
    vector<int> vec;
    void traversal(TreeNode* root) {
        if (root == NULL) return;
        traversal(root->left);
        vec.push_back(root->val);// 将二叉搜索树转换为有序数组
        traversal(root->right);
    }
    bool isValidBST(TreeNode* root) {
        vec.clear();// 不加这句在leetcode上也可以过，但最好加
        traversal(root);
        for (int i = 1; i < vec.size(); i++) {
            if (vec[i] <= vec[i - 1]) return false;// 注意要小于等于，搜索树里不能有相同元素
        }
        return true;
    }
};

把二叉树转变为数组来判断，是最直观的
但其实不用转变成数组，可以在递归遍历的过程中直接判断是否有序

题目陷阱：
（1）不能单纯的比较左节点小于中间节点，右节点大于中间节点就完事

要比较的是左子树所有节点小于中间节点，右子树所有节点大于中间节点

上图不符合二叉搜索树

（2）样例中最小节点可能是int的最小值，如果这样使用最小的int来比较也是不行的

以初始化比较元素为long long的最小值

递归法：
（1）确定递归函数，返回值以及参数
返回值：bool
参数：根节点

long long maxVal = LONG_MIN;
bool isValidBST(TreeNode* root)

（2）确定终止条件

if (root == NULL) return true;

（3）确定单层递归的逻辑
中序遍历，一直更新maxVal，一旦发现maxVal >= root->val，就返回false，注意元素相同时候也要返回false。

bool left = isValidBST(root->left); // 左
// 中序遍历，验证遍历的元素是不是从小到大
if (maxVal < root->val) maxVal = root->val;// 中
else return false;
bool right = isValidBST(root->right);// 右
return left && right;

C++：

class Solution {
public:
    long long maxVal = LONG_MIN;
    bool isValidBST(TreeNode* root) {
        if (root == NULL) return true;
        bool left = isValidBST(root->left); // 左
        // 中序遍历，验证遍历的元素是不是从小到大
        if (maxVal < root->val) maxVal = root->val;
        else return false;
        bool right = isValidBST(root->right); // 右
        return left && right;
    }
};

如果测试数据中有 longlong的最小值，不可能在初始化一个更小的值
建议避免初始化最小值，如下方法取到最左面节点的数值来比较
C++：

class Solution {
public:
	TreeNode* pre = NULL;// 用来记录前一个节点
    bool isValidBST(TreeNode* root) {
		if (root == NULL) return true;
		bool left = isValidBST(root->left);
		if (pre != NULL && pre->val >= root->val) return false;
		pre = root;// 记录前一个节点
		bool right = isValidBST(root->right);
		return left && right;
    }
};

鼓励坚持十七天的自己😀😀😀

文章来源:https://blog.csdn.net/BigDavid123/article/details/135054016
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：veading@qq.com进行投诉反馈，一经查实，立即删除！