12.11图的存储方式（邻接矩阵、邻接表），对应操作（插入，删除，查找），遍历，最小生成树

构建树

先序输入

邻接输入

?图的邻接矩阵

无向图

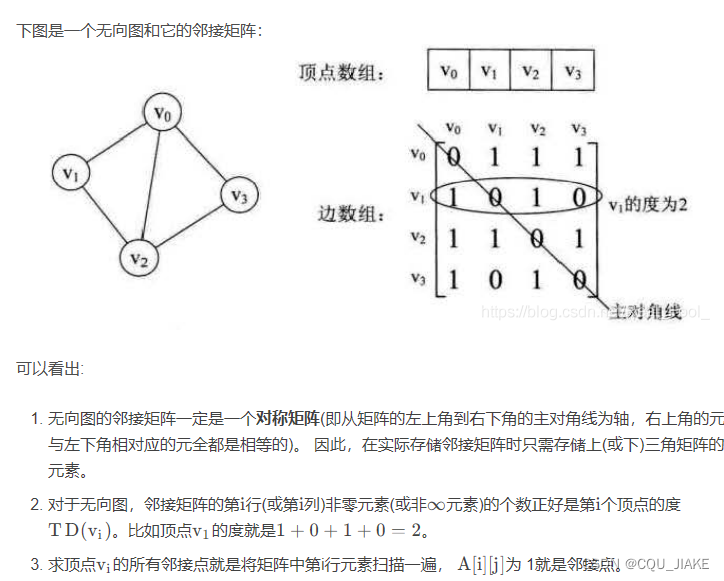
有向图

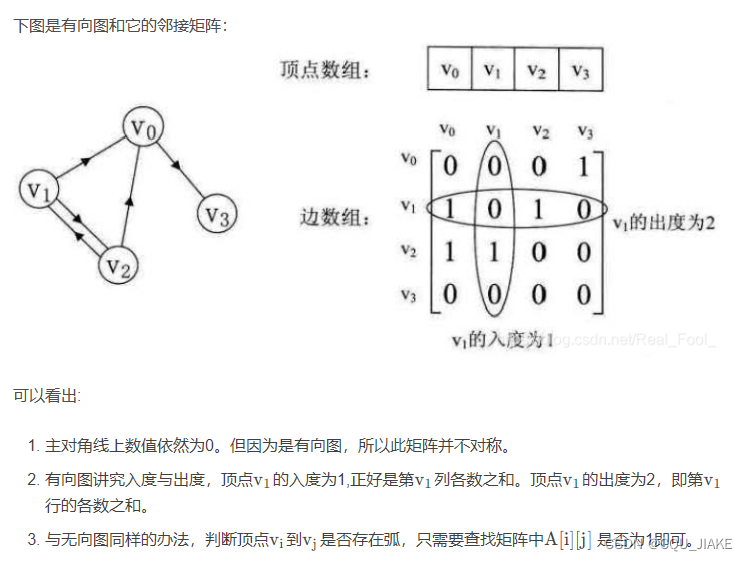
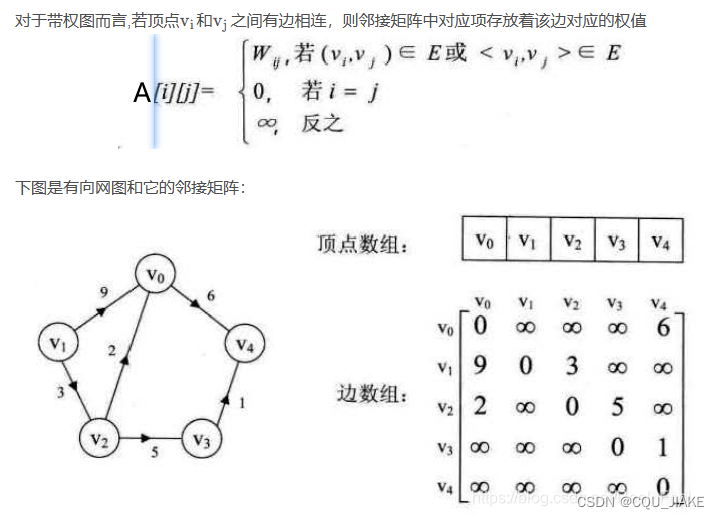
邻接矩阵就是通过顶点数组，直接记录顶点来记录边，即两个顶点数组夹成的二维数组里记录的就是边的信息

#define MaxVertexNum 100	//顶点数目的最大值
typedef char VertexType;	//顶点的数据类型
typedef int EdgeType;	//带权图中边上权值的数据类型
typedef struct{
	VertexType Vex[MaxVertexNum];	//顶点表
	EdgeType Edge[MaxVertexNum][MaxVertexNum];	//邻接矩阵，边表
	int vexnum, arcnum;	//图的当前顶点数和弧树
}MGraph;

图有两个重要参数，即点和边。?

邻接表

其实就是相当于在邻接矩阵的基础上，去掉了那些NULL的结点，对于每个边只保留了非空的结点，也就形成了每个结点下的一串串链

即在顶点链表中，每个顶点有两个指针，一个指针（next)指向后续的顶点（与该顶点不一定连通，只是编号顺序）；一个指针(dest)指向由该顶点通向的后续顶点（与该顶点一定连通）

#define MAXVEX 100	//图中顶点数目的最大值
type char VertexType;	//顶点类型应由用户定义
typedef int EdgeType;	//边上的权值类型应由用户定义
/*边表结点*/
typedef struct EdgeNode{
	int adjvex;	//该弧所指向的顶点的下标或者位置
	EdgeType weight;	//权值，对于非网图可以不需要
	struct EdgeNode *next;	//指向下一个邻接点
}EdgeNode;

/*顶点表结点*/
typedef struct VertexNode{
	Vertex data;	//顶点域，存储顶点信息
	EdgeNode *firstedge	//边表头指针
}VertexNode, AdjList[MAXVEX];

/*邻接表*/
typedef struct{
	AdjList adjList;
	int numVertexes, numEdges;	//图中当前顶点数和边数
}

无向图

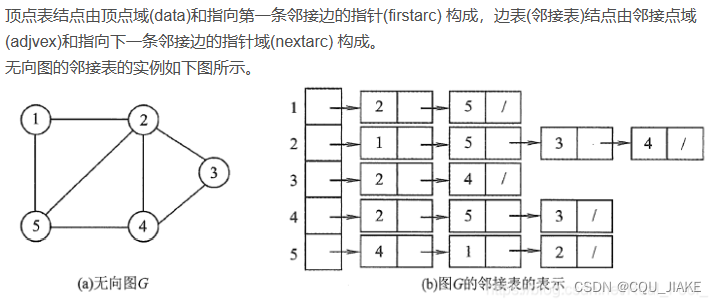
有向图

插入操作

查找操作

这是每个新节点都插入到头部位置?

删除操作

图的遍历

DFS

bool visited[MAX_VERTEX_NUM];	//访问标记数组
/*从顶点出发，深度优先遍历图G*/
void DFS(Graph G, int v){
	int w;
	visit(v);	//访问顶点
	visited[v] = TRUE;	//设已访问标记
	//FirstNeighbor(G,v):求图G中顶点v的第一个邻接点，若有则返回顶点号，否则返回-1。
	//NextNeighbor(G,v,w):假设图G中顶点w是顶点v的一个邻接点，返回除w外顶点v
	for(w = FirstNeighbor(G, v); w>=0; w=NextNeighor(G, v, w)){
		if(!visited[w]){	//w为u的尚未访问的邻接顶点
			DFS(G, w);
		}
	}
}
/*对图进行深度优先遍历*/
void DFSTraverse(MGraph G){
	int v; 
	for(v=0; v<G.vexnum; ++v){
		visited[v] = FALSE;	//初始化已访问标记数据
	}
	for(v=0; v<G.vexnum; ++v){	//从v=0开始遍历
		if(!visited[v]){
			DFS(G, v);
		}
	}
}

应用?

3、深度优先的生成树和生成森林

深度优先搜索会产生一棵深度优先生成树。 当然，这是有条件的，即对连通图调用DFS才能产生深度优先生成树，否则产生的将是深度优先生成森林，如下图所示。基于邻接表存储的深度优先生成树是不唯一的 。（因为邻接表自身存储就不是唯一的）

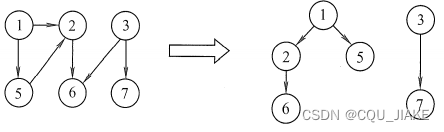
注意：图的邻接矩阵表示是唯一的，但对于邻接表来说，若边的输入次序不同，生成的邻接表也不同。因此，对于同样一个图，基于邻接矩阵的遍历所得到的DFS序列和BFS序列是唯一的，基于邻接表的遍历所得到的DFS序列和BFS序列是不唯一的.

最小生成树

最小生成树是指一个连通无向图中包含所有顶点的树，并且其边的总权重最小。

最小生成树的概念是为了解决一类问题，即在一个连通图中找到一棵包含所有顶点的树，并且使得树的边的权重之和最小。最小生成树在实际应用中有着广泛的应用，例如在电力输送网络中确定最佳输电线路、在城市道路规划中确定最佳道路布局、在通信网络中确定最佳通信线路等。

以城市道路规划为例，假设一个城市有多个区域，我们希望在这些区域之间建立道路，使得每个区域都能够互相到达，并且总的道路长度最小。这就可以通过最小生成树来解决。图中的每个顶点表示一个区域，边的权重表示两个区域之间的道路长度。通过找到最小生成树，就可以确定哪些区域之间需要建立道路，并且选择长度最短的道路，从而实现最优的道路规划。

最小生成树的概念的引入，使得我们能够在图中找到一种最优的连接方式，并且在实际问题中能够进行合理的规划和决策。