12.25~12.27并查集（查找与合并），全排列，约瑟夫问题（队列，数组）upper/lower_bound,重构二叉树，最优矩阵，线段树（构建），淘汰赛（构建树，队列），医院问题（最短路，弗洛伊德

P1551 亲戚（并查集）

题目背景

若某个家族人员过于庞大，要判断两个是否是亲戚，确实还很不容易，现在给出某个亲戚关系图，求任意给出的两个人是否具有亲戚关系。

题目描述

规定：�x?和?�y?是亲戚，�y?和?�z?是亲戚，那么?�x?和?�z?也是亲戚。如果?�x，�y?是亲戚，那么?�x?的亲戚都是?�y?的亲戚，�y?的亲戚也都是?�x?的亲戚。

输入格式

第一行：三个整数?�,�,�n,m,p，（�,�,�≤5000n,m,p≤5000），分别表示有?�n?个人，�m?个亲戚关系，询问?�p?对亲戚关系。

以下?�m?行：每行两个数?��Mi?，��Mj?，1≤��,?��≤�1≤Mi?,?Mj?≤n，表示?��Mi??和?��Mj??具有亲戚关系。

接下来?�p?行：每行两个数?��,��Pi?,Pj?，询问?��Pi??和?��Pj??是否具有亲戚关系。

输出格式

�p?行，每行一个?Yes?或?No。表示第?�i?个询问的答案为“具有”或“不具有”亲戚关系。

题解

注意并查集的合并操作，是要让合并爹的爹，即等式左边为爹，右边为另一联通图的爹

    int f[5005], n, m, p, u, v;//f记录的是联通图的代表点编号
    int find(int x) {//返回的是爹的编号
        if (f[x] == x)return x;
        else {//并且让找到的爹赋值给自己的指针上
            f[x] = find(f[x]);//递归查找f[x]的爹，直到f[x]是自己的爹，等式左边代表指针，等式右边代表实际节点
            return f[x];//返回自己的爹，同时也是这个联通图的代表,经过上一行，就是形成了一层
        }//只管并
    }
    cin >> n >> m >> p;
    for (int i = 1; i <= n; i++)f[i] = i;//并查集最好都有这样一步，不然一开始的话数组存的都是0，也就意味着各个点都是联通的，即每个点都是0号节点的下面一层的儿子
    for (int i = 1; i <= m; i++) {
        cin >> u >> v;
        //f[u] = v;//合并不是这么合并的这样合并只是把u一个点并到V的连通图上了，应该是要把U这一组的所有的点都并到v上，就是让这个组的代表点爹成为v，这样才是正确的合并
        f[find(u)] = find(v);//并查集合并还得是这么合并，即让代表点的爹成为另一个代表点，随便并会MLE，不知道问题在哪
    }
    for (int i = 1; i <= p; i++) {
        cin >> u >> v;
        if (find(u) == find(v))cout << "Yes" << endl;
        else cout << "No" << endl;
    }

P1706 全排列问题

按照字典序输出自然数?11?到?�n?所有不重复的排列，即?�n?的全排列，要求所产生的任一数字序列中不允许出现重复的数字。

int used[11], n;
bool vis[11];
void dfs(int k) {//这个参数可以有两种含义，不同的含义有不同的写法
    if (k == n) {//这种是视为已确定的位数，还有一种理解是要确定某位，即指向要确定的位数，而这种是代表已确定的位数，指向的是已经确定的
        for (int i = 1; i <= k; i++) {
            cout << "     " << used[i];
        }
        cout << endl;
        return;
    }
    for (int i = 1; i <= n; i++) {
        if (!vis[i]) {
            used[++k] = i;
            vis[i] = 1;
            dfs(k);
            k--;
            vis[i] = 0;
        }
    }
}
cin >> n;
dfs(0);

P1996 约瑟夫问题?

数组模拟

#include<stdio.h>
#include<iostream>
#include<string>
#include<stack>
#include<vector>
#include<cmath>
#include<queue>
#include<iomanip>
using namespace std;
//
int nxt[105];
int n, m;
int main() {
    cin >> n >> m;
    for (int j = 1; j <= n; j++) {
        nxt[j] = j + 1;
    }
    nxt[n] = 1;
    int i = n;//i指的是当前这个人的前一个人
    while (n) {
        int t = 1;//把第一个人算上
        while (t < m) {
            t++;
            i = nxt[i];
        }
        cout << nxt[i]<<" ";//此时出来时就是最后一个人，
        nxt[i] = nxt[nxt[i]];
        n--;
    }
    return 0;
}

队列?

#include <iostream>
#include <vector>
#include <algorithm>
#include<stack>
#include<queue>
#include <map>
#include<string>
using namespace std;
//队列模拟约瑟夫问题，如果队头元素此时为要出局的数字，那么就出局，不然就移到队尾循环
int main() {
    queue<int>q;
    int n, m, cnt = 0;//取模M的话，cnt在0~M-1内循环
    cin >> n >> m;//cnt为当前队头小孩要喊的数字
    for (int i = 1; i <= n; i++)q.push(i);
    while (!q.empty()) {
        if (cnt == m - 1) {//当前小孩喊的要被淘汰
            cout << q.front() << " ";
            q.pop();
            cnt = 0;
        }
        else {//当前小孩不淘汰
            cnt++;//是下个小孩要喊的数字
            q.push(q.front());
            q.pop();
        }
    }
    return 0;
}

P2249 【深基13.例1】查找

快速写入&&STL的lower_bound

STL自带lower_bound,返回的是地址，可以用它在数组上。如果要得到数组下标，由于返回的是地址，所以还需要再减去数组名，即数组开始的地址

int read() {
    int x = 0, f = 1;
    char c = getchar();
    while (c < '0' || c>'9') {
        if (c == '-')f = -1;
        c = getchar();
    }
    while (c >= '0' && c <= '9') {
        x = x * 10 + c - '0';
        c = getchar();
    }
    return x * f;
}//所谓快速写入，实际上就是把输入数字型，转化为输入字符型，通过对字符的输入得到数字，可能会更快
const int maxn = 1e6 + 4;
int n, m, a[maxn];
n = read(), m = read();
for (int i = 1; i <= n; i++)a[i] = read();
while (m--) {
    int x = read();
    int ans = lower_bound(a + 1, a + n + 1, x) - a;
    if (x != a[ans])cout << -1;
    else cout << ans;
    cout << " ";
}

重构二叉树

105.已知前序与中序

通过前序找到根，然后在中序中找个这个根的位置，确定这个根的左子树与右子树大小，接着递归相应区间

class Solution {
    private:
    unordered_map<int,int>index;
public:
TreeNode*mybuild(const vector<int>&preorder,const vector<int>&inorder,int pl,int pr,int il,int ir){
    if(pl>pr){return nullptr;}
    int proot=pl;//先序的根节点编号
    TreeNode*root=new TreeNode(preorder[pl]);
    int iroot=index[preorder[proot]];//从Index找，找先序序列的根节点的编号
    int sizel=iroot-il;//proot是下标，p[proot]是值，就是查找指定的值出现的下标，在中序序列中
    root->left=mybuild(preorder,inorder,pl+1,pl+sizel,il,iroot-1);//左子树大小，不包含根节点，即区间的右端点，所以不用+1
    root->right=mybuild(preorder,inorder,pl+sizel+1,pr,iroot+1,ir);
    return root;
}
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int n=preorder.size();
        for(int i=0;i<n;i++){
            index[inorder[i]]=i;//中序序列第i个出现的元素，的哈希映射为i
        }
        return mybuild(preorder,inorder,0,n-1,0,n-1);
    }
};

56.合并区间

把每个区间的起点从小到大排序，然后记录此时的最右区间，如果此时起点比它小，那就能合并，合并的时候更新最右区间；直到起点不比它小，然后把最早起点和此时最右区间导出，然后更新最早起点为这个，然后最右区间为这个的

class Solution {
public:
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        if(!intervals.size()){
            return {};
        }
        sort(intervals.begin(),intervals.end());
        vector<vector<int>>res;
        for(int i=0;i<intervals.size();i++){
            int l=intervals[i][0],r=intervals[i][1];
            if(!res.size()||res.back()[1]<l){
                res.push_back({l,r});
            }else{
                res.back()[1]=max(res.back()[1],r);
            }
        }
        return res;
    }
};

88.合并两个有序数组

双指针从大的地方开始，就是先扫描大的，然后逐个放到第一个数组的末尾

最优矩阵

    const int maxn = 125;
    int arr[maxn][maxn], n, ans = 0;
    cin >> n;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            cin >> arr[i][j];
        }
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            arr[i][j] = arr[i][j] + arr[i - 1][j] + arr[i][j - 1] - arr[i - 1][j - 1];
        }
    }
    for (int i = 1; i <= n; i++) {//右下x
        for (int j = 1; j <= n; j++) {//右下y
            for (int k = i; k <= n; k++) {//左上x
                for (int m = j; m <= n; m++) {//左上y
                    ans = max(ans, arr[k][m] - arr[i - 1][m] - arr[k][j - 1] + arr[i - 1][j - 1]);
                }
            }
        }
    }
    cout << ans;

P4715 【深基16.例1】淘汰赛

队列模拟

先用队列保存原始数据，然后不断的缩减，依据规则，最后只保留出顶点

这种特点，就适用于那些中间节点没什么用，只是在构建过程的中间步骤的过程，比如哈夫曼树的构建，或者是中间过程不需要保存（需要输出时就是到了输出就行），

对比约瑟夫问题的队列模拟

#include <iostream>
#include <vector>
#include <algorithm>
#include<stack>
#include<queue>
#include <map>
#include<string>
#include<cstdio>
using namespace std;
int main() {
    int n;
    queue<pair<int, int>>q;
    cin >> n;
    for (int i = 1; i <= (1 << n); i++) {
        int x;
        cin >> x;
        q.push({ i,x });
    }
    while (q.size() > 2) {
        pair<int, int>x, y;
        x = q.front();
        q.pop();
        y = q.front();
        q.pop();
        if (x.second > y.second) {
            q.push(x);
        }
        else {
            q.push(y);
        }
    }
    pair<int, int>x, y;
    x = q.front();
    q.pop();
    y = q.front();
    q.pop();
    if (x.second > y.second) {
        cout << y.first;
    }
    else {
        cout << x.first;
    }
    return 0;
}

建树

依据规则构建一棵树结构，然后每个父亲结点是两个孩子结点的最大值

依据规则去建树，就是由两个结点去合并，然后有一定的合并规则，递归合并完后就是最后的规则树，线段树的规则是区间里两个相邻结点的加和

#include <iostream>
#include <vector>
#include <algorithm>
#include<stack>
#include<queue>
#include <map>
#include<string>
#include<cstdio>
using namespace std;
struct node {
    int power, id;
};
node maxt(node a, node b) {
    return a.power > b.power ? a : b;
}
node mint(node a, node b) {
    return a.power < b.power ? a : b;
}
node a[150], tree[600];//原始数据就是规则树的叶子结点，然后在依据规则构造树的过程中，会产生非叶子结点，所以树要多开空间，一般多开4倍
void build(int node, int start, int end) {
    if (start == end) {
        tree[node] = a[start];
        return;//叶子结点，数据就是原始数据
    }//往下是非叶子结点，就要依据叶子结点来构造
    int l = node * 2, r = node * 2 + 1, mid = (start + end) / 2;//之所以要找中点，就是因为是依据一个规定好的区间来构建的
    build(l, start, mid);
    build(r, mid + 1, end);
    tree[node] = maxt(tree[l], tree[r]);
}
int main() {
    int n;
    cin >> n;
    for (int i = 1; i <= (1<<n); i++) {
        cin >> a[i].power;
        a[i].id = i;
    }
    build(1, 1, (1 << n));
    cout << mint(tree[2], tree[3]).id;//输入的时候是在a上，输出的时候在tree上，即build是在tree上做的修改
    return 0;
}

线段树

结合了二叉树与前缀和

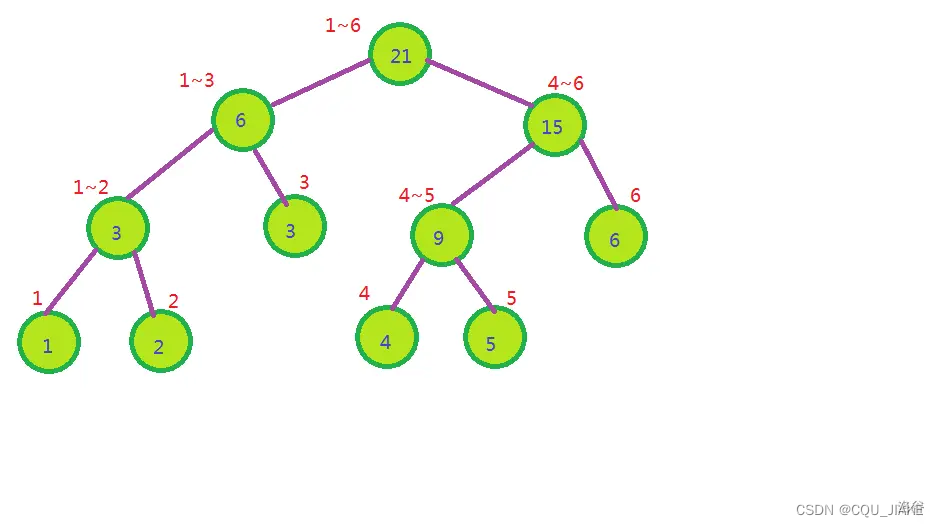
每个父节点是它的两个子节点的值的和！

修改和查询的时间复杂度都为Ologn

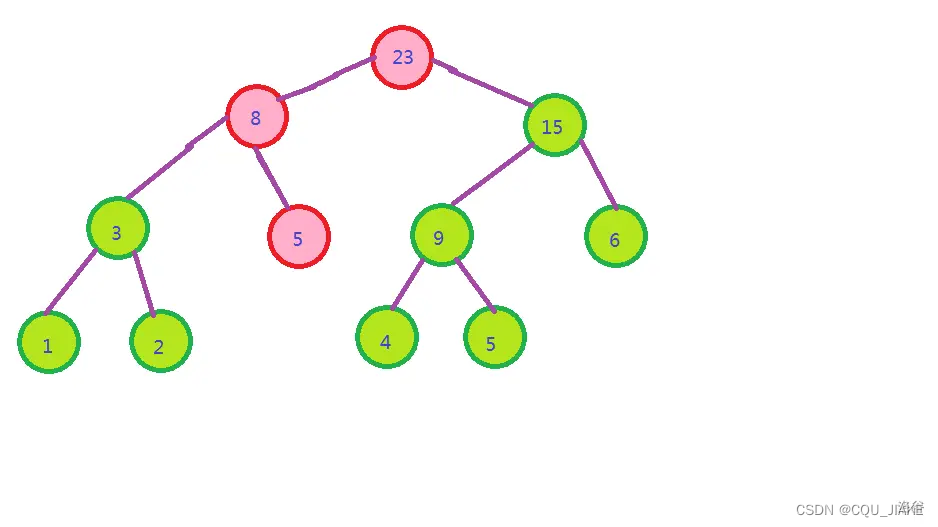
修改就是从根节点往下查找，找到结点2然后加上3，再往上顺着一个一个改

查询，查询2~5的和

2~5的和

=2~3的和+4~5的和

=2+3+4~5的和

=2+3+9

=14

总之，就是沿着线段树的划分把区间分开，再加到一块就行啦！

完全二叉树，数组顺序存储

?

typedef long long ll;
const int maxn = 1e5 + 10, maxm = 5e5 + 5;
ll arr[maxn] = { 0 }, tree[maxm] = { 0 };//arr原始数据，tree为存线段树的数组
void build(int node, int start, int end) {//根节点以及左右区间
    if (start == end) {
        tree[node] = arr[start];//存数据
        return;
    }
    int left = node * 2, right = node * 2 + 1, mid = (start + end) / 2;
    build(left, start, mid);//左与右是树结点的属性
    build(right, mid + 1, right);//s,end,与midd是指的区间
    tree[node] = tree[left] + tree[right];
}
void update(int node, int start, int end, int id, int val) {//依据区间构建出的一棵树
    if (start == end) {
        tree[node] += val;
        return;//找到头后进行更新
    }
    int left = node * 2, right = node * 2 + 1, mid = (start + end) / 2;
    if (id >= start && id <= mid)update(left, start, mid, id, val);//
    else update(right, mid + 1, end, id, val);//沿着路径去查找
    tree[node] = tree[left] + tree[right];//最后更新路径上的结点值，所以它的更新复杂度为logn
}//之所以和中点比较，是因为线段树的左右子树的构建是直接切区间中点的，左半区间代表左子树，右半区间为右子树
//如果查询区间涵盖住了整个子树，那么直接加上子树的根节点值
//其他情况就是不完全涵盖，有交集，有交集的话就要加上这个子树上的部分区间和
//而要获取具体是这个子树的哪段区间，就需要先和这段子树的中间值去比较，递归下去，划分这个子树为左子树右子树，看看涵盖的区间包括其中哪个
//如果包含左子树，那么查询区间的左端点一定比这段树的中间端点小
//如果包含右子树，那么查询区间的右端点一定比这段树的区间的中间端点大
int query(int node, int start, int end, int l, int r) {//查询l和r上的区间和
    if (l <= start && r >= end)return tree[node];//是树的区间被查询区间包含了，而不是查询区间被包含了
    int left = node * 2, right = node * 2 + 1, mid = (start + end) / 2;
    int sum = 0;
    if (l <= mid)sum += query(left, start, mid, l, r);//如果查询左区间在树的中间区间左侧，那么递归更新树的左区间不变，右区间为中间点
    if (r > mid) sum += query(right, mid + 1, end, l, r);
    //由于进一步划分了范围，所以树所代表的区间一定会越来越小，直到小到被查询区间所涵盖，在这一过程中，查询区间是不变的
    //变的是递归的子树的区间范围
}

?P1229 遍历问题

只有一个儿子的节点才会在前序后序的情况下有不同的中序遍历，所以问有多少种不同的情况，就是问只有一个儿子的节点个数

前序出现AB，后序出现BA，就说明这个节点只有一个儿子。这个节点有两种中序，及左右儿子

应用乘法，每层的左右儿子情况相互独立，相互独立，所以是乘法，上面的不会影响下面的，就是每层的情况，每层只有一个儿子

所以就是遍历，找AB,BA结构

比如abc,cba,那就是c是b的儿子，b是a的儿子，但是具体是左还是右儿子不能确定，只知道树的高度为3，而且每层只有1个儿子，所以结果就是1<<2

#include <iostream>
#include <vector>
#include <algorithm>
#include<stack>
#include<queue>
#include <map>
#include<string>
#include<cstdio>
using namespace std;
int main() {
    string a, b;
    cin >> a >> b;
    int ans = 0;
    for (int i = 0; i < a.length(); i++) {//i模拟先序里根的位置
        for (int j = 1; j < b.length(); j++) {//j模拟后序里根的位置
            if (a[i] == b[j] && a[i + 1] == b[j - 1])ans++;
        }
    }
    cout << (1 << ans);//直接用移位，就可以兼顾0的情况与后续所有情况
    return 0;
}

P1102 A-B 数对

就是说，有N个数，然后要让计算结果为C，两个数的计算结果，

先排序，然后让最大去减最小，如果结果大于C，就左移右指针，如果结果小于C，就右移左指针，直到最后两指针相遇

转换为A-C=B

映射的原理就是C是输入的固定常数，那么A与B之间就可以建立起一个一一映射的关系

首先对A数组每个元素出现的次数统计起来，用map映射，最后将A数组每次减一个C，再扫一遍，将所有映射的次数和加起来就是答案

是给定一个数组，问这个数组里相减是C的组合次数，所以找元素的时候也是在自己的数组里去找，就是只有一个数组为A

#include <iostream>
#include <vector>
#include <algorithm>
#include<stack>
#include<queue>
#include <map>
#include<string>
#include<cstdio>
using namespace std;
typedef long long ll;
ll a[200001];
map<ll, ll>m;
int main() {
    int n;
    ll c, ans = 0;
    cin >> n >> c;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        m[a[i]]++;//a[i]是元素，mai是它出现的次数，频数
        a[i] -= c;//这个元素要和另一个数相减结果为C，那么将原数据转换为这个数
    }
    for (int i = 1; i <= n; i++)ans += m[a[i]];//将映射结果再逐次相加得到
    cout << ans << endl;
    return 0;
}

lower_bound/upper_bound

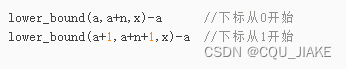
lower找的是第一个大于等于的查找值x的数的地址，要减去数组名a，才是数组里的下标

涵盖等于的部分

upper找到是第一个大于的

在a里找第一个大于a[i]+c的数字出现的下标，再找第一个大于等于a[i]+c的数字出现的下标（这个数字应该是要等于a[i]+c的)，它们做差，就是这个区间的长度，也就是区间里不含一侧端点的元素个数，即等于a[i]+c的元素个数

就是先排个序，然后从头开始，对每个元素a[i],都找a[i]+c出现的次数即可

P4913 【深基16.例3】二叉树深度

主要是怎么依据这个输入方式构建树

用结构体，里面的指针为int型来构建

const int maxn = 1e6 + 10;
struct node {
    int l, r;//既然输入的是左右孩子的编号，那么左右孩子的指针类型就直接设置为Int即可
}t[maxn];//用数组存树的节点，那么下标就是树节点编号
int n;
int dfs(int id) {
    if (id == 0)return 1;//到了叶子节点
    return max(dfs(t[id].l), dfs(t[id].r)) + 1;
}
cin >> n;
for (int i = 1; i <= n; i++) {
    cin >> t[i].l >> t[i].r;//直接顺序输入树的左右孩子编号
}
cout << dfs(1) - 1;

P1305 新二叉树

主要问题在于怎么存树，由于输入为

输入三个char，直接让char作为下标，然后它的左右孩子为后面的两个字符

struct p {
    char lc, rc;
}t[130];
char h, h1;
void sm(char x) {
    if (x == '*')return;
    cout << x;
    sm(t[x].lc);
    sm(t[x].rc);
}
int n;
cin >> n;
cin >> h1 >> t[h1].lc >> t[h1].rc;
for (int i = 1; i < n; i++) {
    cin >> h >> t[h].lc >> t[h].rc;
}
sm(h1);

bits/stdc++.h?

P1364 医院设置

树的重心的定义：

树若以某点为根，使得该树最大子树的结点数最小，那么这个点则为该树的重心，一棵树可能有多个重心。

树的重心的性质：

1、树上所有的点到树的重心的距离之和是最短的，如果有多个重心，那么总距离相等。

2、插入或删除一个点，树的重心的位置最多移动一个单位。

3、若添加一条边连接2棵树，那么新树的重心一定在原来两棵树的重心的路径上

应用最短路（弗洛伊德）

用最短路的话，就是先得到树的各个节点到其他节点的最短路径长度，然后外层循环为起点，即医院设置的位置，内层循环为终点，加上路径长度乘以终点的权值

弗洛伊德的算法就是应用动态规划的思想，即母问题是可以应用所有的点作为终点站，那么划分子问题就是，逐渐减少可应用的终点站的数量，或者就是从一开始只能应用一个中转站，然后在此基础上，逐渐增加可用中转站的数量（数组记录之前中转站保存的最好结果），最后直到增加到可用全部的中转站，也就是说最外层的循环代表的实际就是考虑的问题规模，只不过一开始时是从最小的问题规模考虑的，而且每次只增加一层问题规模，逐渐累积才到最后的大问题规模

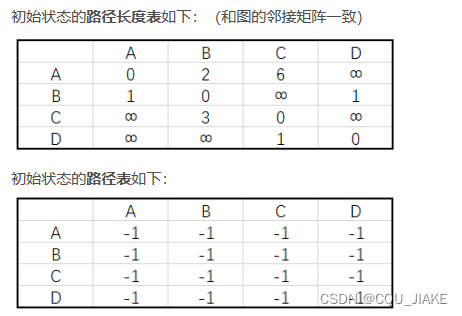
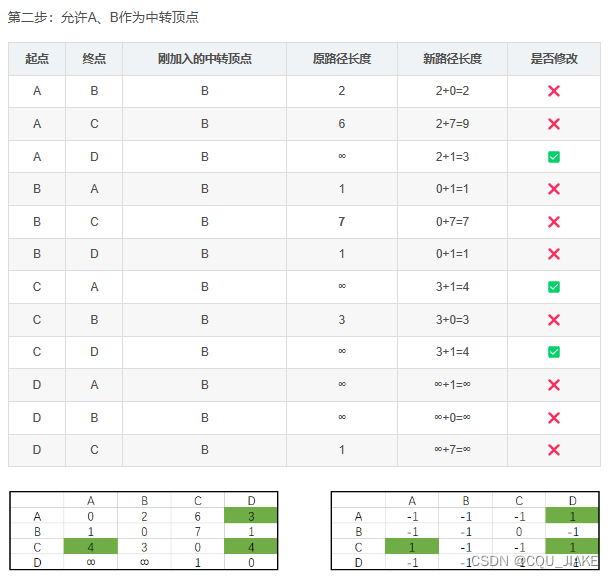
在用新k时，由于比较的是d[i][k]+d[k][j]，而d[i][k],d[k][j]都是带k的，是不会变的，即d[i][k]=d[i][k]+d[k][k],d[k][j]=d[k][k]+d[k][j]，所以在每个k的遍历各个起点与终点过程中，顺序问题不会影响，就是因为在过程中，d[i][k],d[j][k]都不会变，都是保留上一层里的结果，用的之前的最好结果，然后用这个点，可能去缩短结果

可以发现如果中专点与起点相同，那么g[i][k]=0,也就等于原来保存的最优路径长度，所以在循环内层，i==k的情况可直接剪掉

如果中转点与终点相同，那么g[k][j]=0,还是等于原来保存的最优路径长度，但这是对每个起点而言的，就是说过程是外层为中转点循环，内一层为起点循环，最里层为终点循环

在起点循环时，遍历所有这个起点的终点，如果起点和中转点相同就没必要继续，剪掉这一次的循环，相当于是扫了三次数组，第一次扫确定中转点，然后在确定中转点的基础上去确定起点，然后在确定中转点与起点的基础上，去枚举终点，通过中转点

需要注意的是，在每个问题规模下，各个起点与终点的组合都会被访问一遍，即都会被再确认一遍

初始的路径矩阵，就是一开直接相连的矩阵；

后续扩大问题规模，每扩大一次规模，就是原矩阵，即原起点终点矩阵对，在原来的最好方法基础上，再应用此时的新问题条件，可以得到的最优解法

考虑一个问题，就是某个起点一开始是无法到达中转点，即g[i][k]=inf,即一开始无法一步到达，但是后续通过其他点可以到达，到达后可依据这个中转点更新路径长度

中转点 的 个数 可能需要多个 ,?A 到 B 可能中间途径多个 中转点?, 使得 两个结点 之间的距离更短

每个顶点 都有可能 缩短 另外两个 顶点 之间的距离 ;

只允许经过 1 号点中转得到任意两点之间的最短路径

在之前的基础上-只允许经过 1、2 号点中转得到任意两点之间的最短路径

任意一个顶点都有可能作为其他任意两顶点间最短路径的中转点，以更新两顶点间的更短路径，且中转点的顺序交换没有影响，通过依次使n个顶点充当一次中转点以求解任意顶点间的最短路径。

若将B称为一级中转点，那么A通过一级中转点B获取到达顶点C的更短路径。

图解（2）即使B没有作为以及中转点，其依旧有可能充当其他级别的中转点。

由图可见，即使B没有作为A到C的一级中转点（直接中转），但是B作为D到C的一级中转点，为A借助中转点D获取到达C的更短路径打下了基础

比如一条很长的链，最后确定就是，先到距离终点最近的那个节点，然后通过那个节点到终点，而到距离终点最近的那个节点的路径长度，需要通过其他的中转站，这个是在其他的中转站循环里完成的

每个点都有可能成为缩短其它任意两节点之间路径长度的中转点，

担心的是确实是可以缩短，但是不可达，

A要到C，可以通过A,C之间的点到C，就是D，如果A能到C，但是A不能直接到C，就说明A和C之间一定有割点，通过中转点循环，可以找到割点到终点的最短路径

可见，每一个顶点都有可能作为任意两点的直接或间接中转点，因此主循环需要循环n次，依次将图中的顶点vk作为其余顶点间的路径<vi,vj>的中转点，判断该顶点是否可以作为<vi,vj>的中转点。若可以，则更新<vi,vj>的最短路径。其数学表达式为，假设Dis(vi,vj)表示顶点vi到顶点vj的路径权值，假如Dis(vi,vj)>Dis(vi,vk)+Dis(vk,vj)，则Dis(vi,vj)=Dis(vi,vk)+Dis(vk,vj)。
各个顶点充当中转点的顺序不影响求解任意顶点间最短路径的效果。如图（2）所示，若B先充当中转点再到D，则D先通过B连通C，即D->B->C。再到D充当中转点时，A通过D连通C，即A->D->B->C为最短路径；若D先充当中转点再到B，则A先通过D连通B，即A->D->B.再到D通过B连通C，即A->D->B->C.可见，各个顶点充当中转点的顺序不影响求解任意顶点间最短路径的效果。

对于A到C；如果B先作为中转点，则A不会先到C，但是D可以以B为中转点找一个最短路劲到C，然后D再作为中转点，对于A到C可以通过中转点D到；如果D先作为中转点，A可以通过D先到C，然后还可以更新A到B的最短路径，然后B再作为中转点，可以以B为中转点，通过A到B的距离到C?

    int a[101], g[101][101], n, l, r, mina = 1e9, total = 0;
    cin >> n;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            g[i][j] = 1e9;//gij代表两点之间的路径数量
        }
    }
    for (int i = 1; i <= n; i++) {
        g[i][i] = 0;
        cin >> a[i] >> l >> r;
        if (l)g[i][l] = g[l][i] = 1;
        if (r)g[i][r] = g[r][i] = 1;
    }
    for (int k = 1; k <= n; k++) {//借助的中间节点
        for (int i = 1; i <= n; i++) {
            if (i != k) {//起点与中间路径不同
                for (int j = 1; j <= n; j++) {
                    if (i != j && k != j && g[i][k] + g[k][j] < g[i][j]) {//如果先到k再到j的代价比先
                        g[i][j] = g[i][k] + g[k][j];
                    }
                }
            }
        }
    }
    for (int i = 1; i <= n; i++) {//把医院建在i处，起点就是i
        total = 0;//重置此时的总成本
        for (int j = 1; j <= n; j++) {//遍历终点为1~n,得到起点到终点的路径
            total += g[i][j] * a[j];//加上每个节点的成本
        }
        mina = min(mina, total);
    }
    cout << mina;

P3371 【模板】单源最短路径（弱化版）

dij算法，堆优化

#include <iostream>
#include <vector>
#include <algorithm>
#include<stack>
#include<queue>
#include <map>
#include<string>
#include<cstdio>
using namespace std;
//fu表示以u为根的总距离，sizeu为u为根的子树大小，是子树的大小
const int maxn = 1e4 + 5, maxm = 5e5 + 4, inf = 1e9;
struct edge {
    int v, w, next;
}e[maxm];
int head[maxn], dis[maxn], n, m, s, cnt = 0;
bool vis[maxn] = { 0 };
void add(int u, int v, int w) {
    e[++cnt].v = v;
    e[cnt].w = w;
    e[cnt].next = head[u];
    head[u] = cnt;
}
typedef pair<int, int> pii;
priority_queue<pii, vector<pii>, greater<pii>>q;
int main() {
    cin >> n >> m >> s;
    for (int i = 1; i <= m; i++) {
        int u, v, w;
        cin >> u >> v >> w;
        add(u, v, w);
    }
    for (int i = 1; i <= n; i++)dis[i] = inf;
    dis[s] = 0;
    q.push({ 0,s });
    while (!q.empty()) {
        int cur = q.top().second, d = q.top().first;
        q.pop();
        if (vis[cur])continue;
        vis[cur] = 1;
        dis[cur] = d;
        for (int i = head[cur]; i; i = e[i].next) {
            int v = e[i].v;
            if (dis[v] > dis[cur] + e[i].w)q.push({ dis[cur] + e[i].w ,v });
        }
    }
    for (int i = 1; i <= n; i++) {
        if (dis[i] >= inf)cout << (1 << 31) - 1 << " ";
        else cout << dis[i] << " ";
    }
    return 0;
}