leetcode刷题记录06（2023-04-19）【验证二叉搜索树(前序遍历) | 对称二叉树(不要闹，递归最简单) | 二叉树的层序遍历(队列/不断清空序列) | 二叉树的最大深度(队列)】

98. 验证二叉搜索树

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

输入：root = [2,1,3]
输出：true

示例 2：

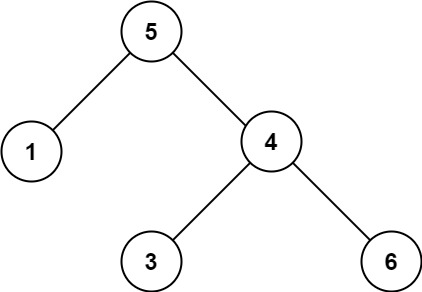
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：
树中节点数目范围在$[1,10^4]$ 内
$?2^{31}<=Node.val<=2^{31}?1$

最开始采用的方法是，通过递归遍历，来判断二叉搜索树是否满足局部排序，但是这种方法，不好考虑到全局是否可行，比如下面这棵树。

		5
	  /	  \
	4		6
		  /   \
		3       7

这棵树就不是一颗符合条件的二叉搜索树，但是，我如果使用注释的方法，返回的结果就是true（因为他没有考虑到5和3的关系）。

代码如下：

class Solution {
    void digui(TreeNode* root, vector<int>& vec) {
        if (root->left != nullptr) {
            digui(root->left, vec);
        }
        vec.push_back(root->val);
        if (root->right != nullptr) {
            digui(root->right, vec);
        }
    }
public:
    //bool isValidBST(TreeNode* root) {
    //    if (root == nullptr) {
    //        return true;
    //    }

    //    if (root->left != nullptr && root->val < root->left->val) {
    //        return false;
    //    }
    //    else {
    //        bool res = isValidBST(root->left);
    //        if (res == false)return false;
    //    }

    //    if (root->right != nullptr && root->val > root->right->val) {
    //        return false;
    //    }
    //    else {
    //        bool res = isValidBST(root->right);
    //        if (res == false)return false;
    //    }

    //    return true;
    //}

    bool isValidBST(TreeNode* root) {
        vector<int> vec;
        digui(root, vec);
        for (int i = 1; i < vec.size(); i++) {
            if (vec[i] <= vec[i - 1]) {
                return false;
            }
        }
        return true;
    }
};

101. 对称二叉树

给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

树中节点数目在范围 [1, 1000] 内
-100 <= Node.val <= 100

第一种方法为 递归 的方法，思路就是，搞两个指针 left 和 right 然后分情况讨论：

• 如果他俩有一个空指针了，另外一个必须也是。是返回true，不是返回false。
• left->val 和 right->val 不相等，很显然返回false
• 如果上面的都满足了，递归调用，判断 left->left 和 right->right 是否对称，同时判断 left->right 和 right->left 是否对称。

语言有些抽象，代码如下：

struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};
 
class Solution {
    bool testIsSame(TreeNode* left, TreeNode* right) {
        if (left == nullptr || right == nullptr) {
            if (left == right) {
                return true;
            }
            else {
                return false;
            }
        }
        if (left->val != right->val) {
            return false;
        }
        else {
            return testIsSame(left->left, right->right) && testIsSame(left->right, right->left);
        }
    }
public:
    bool isSymmetric(TreeNode* root) {
        bool isSame = testIsSame(root->left, root->right);
        return isSame;
    }
};

迭代的方法，如下，主要利用了 stack 这一数据结构。搞两个栈，宏观来讲，我们比较的就是 root->left 和 root->right 是否对称。因此，我们用两个栈来对他们分别进行存储。

这里遍历采用层次遍历的方法，前序遍历和中序遍历用迭代法有点绕，后续遍历更加绕，在此不在使用。遇到前、中、后序遍历的用递归法更加简单直接。

#include<stack>
using namespace std;

class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        TreeNode* left = root->left;
        TreeNode* right = root->right;

        stack<TreeNode*> stk_left;
        stack<TreeNode*> stk_right;
        if (left != nullptr)
            stk_left.push(left);
        if (right != nullptr)
            stk_right.push(right);
        
        while (!stk_left.empty() && !stk_right.empty())
        {
            left = stk_left.top();
            stk_left.pop();


            right = stk_right.top();
            stk_right.pop();

            if (left->val != right->val) {
                return false;
            }

            if (left->left != nullptr && right->right != nullptr) {
                stk_left.push(left->left);
                stk_right.push(right->right);
            }
            else {
                if (left->left != right->right) {
                    return false;
                }
            }

            if (left->right != nullptr && right->left != nullptr) {
                stk_left.push(left->right);
                stk_right.push(right->left);
            }
            else {
                if (left->right != right->left) {
                    return false;
                }
            }
        }
        if (!stk_left.empty() || !stk_right.empty()) {
            return false;
        }
        else {
            return true;
        }
    }
};

同时，递归方法相比于迭代方法性能并没有差很多，甚至更好一些（当然可能和我使用的层次遍历与测试用例分布的情况有关）。但至少可以说明，不会相差太多。

提交记录如下：

从执行时间和内存消耗两方面来看，递归方法看起来更有优势。

102. 二叉树的层序遍历

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

示例 2：
输入：root = [1]
输出：[[1]]

示例 3：
输入：root = []
输出：[]

提示：
树中节点数目在范围 [0, 2000] 内
$?1000<=Node.val<=1000$

这道题目运用队列进行层次遍历。

主要思想是对深度进行一个记录。

后面利用深度信息对节点进行填充。

#include<vector>
#include<queue>
using namespace std;

// Definition for a binary tree node.
struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};
 
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        // 如果为 0 层二叉树，直接返回空 vector
        if (root == nullptr) {
            return {};
        }
        vector<int> deep;       // 用来记录每个节点的深度
        int index = -1;         // 用来记录当前节点的序号（从 0 开始
        deep.push_back(0);  // 第一个节点记录为 0

        queue<TreeNode*> que;   // 存储节点的队列

        que.push(root);     // 放入根节点

        TreeNode* cur = nullptr; // 当前访问到的节点

        vector<int> vec;         // 从前往后存储节点
        while (!que.empty()) {
            index++;
            cur = que.front();
            vec.push_back(cur->val); // 记录节点值
            que.pop();
            if (cur->left != nullptr) {
                que.push(cur->left);
                deep.push_back(deep[index] + 1); // 记录层数
            }
            if (cur->right != nullptr) {
                que.push(cur->right);
                deep.push_back(deep[index] + 1); // 记录层数
            }            
        }

        // 数组 1 维长度应该为树的深度 deep[index] + 1
        vector<vector<int>> result(deep[index] + 1, vector<int>());
        for (int i = 0; i < vec.size(); i++) {      // 再次遍历所有节点
            result[deep[i]].push_back(vec[i]);  // 按照深度进行数组的填充
        }
        return result;
    }
};

104. 二叉树的最大深度

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，

    3
   / \
  9  20
    /  \
   15   7

返回它的最大深度 3 。

主要思路为每次输出每一层的节点，然后加入下一层的节点，很巧妙。

代码如下：

#include<queue>
using namespace std;
// Definition for a binary tree node.
struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};
 
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (root == nullptr) {
            return 0;
        }
        queue<TreeNode*> que;
        que.push(root);
        int deep = 0;
        TreeNode* cur = nullptr;
        while (!que.empty())
        {
            deep++;
            int n = que.size();
            for (int i = 0; i < n; i++) {
                cur = que.front();
                que.pop();
                if (cur->left != nullptr) {
                    que.push(cur->left);
                }
                if (cur->right != nullptr) {
                    que.push(cur->right);
                }
            }
        }
        return deep;
    }
};

利用这道题的思路可以对上面题目 102 题很好地进行改进了。