Python - 深夜数据结构与算法之 Disjoint-Set
目录
一.引言
这里并查集不是我们集合中提到的并集、差集,可能很多同学都是第一次接触这个概念,博主也是,不过其确实涉及到一些集合的操作和概念,下面我们看下什么是并查集。
二.并查集简介
1.使用场景
并查集 disjoint-set [非交集数据结构] 主要用于解决组团、配对问题 即 Group or not,主要是快速判断当前的两个元素是不是在同一个集合中。
其常见于社群场景,例如朋友圈你们是否互为好友。

- makeSet:?新建一个并查集
- unionSet: x、y 分别对应两个群组,将各自对应的群组进行合并
- find: 找到元素 x 所在群组或者集合的代表
2.常规操作
◆ 初始化
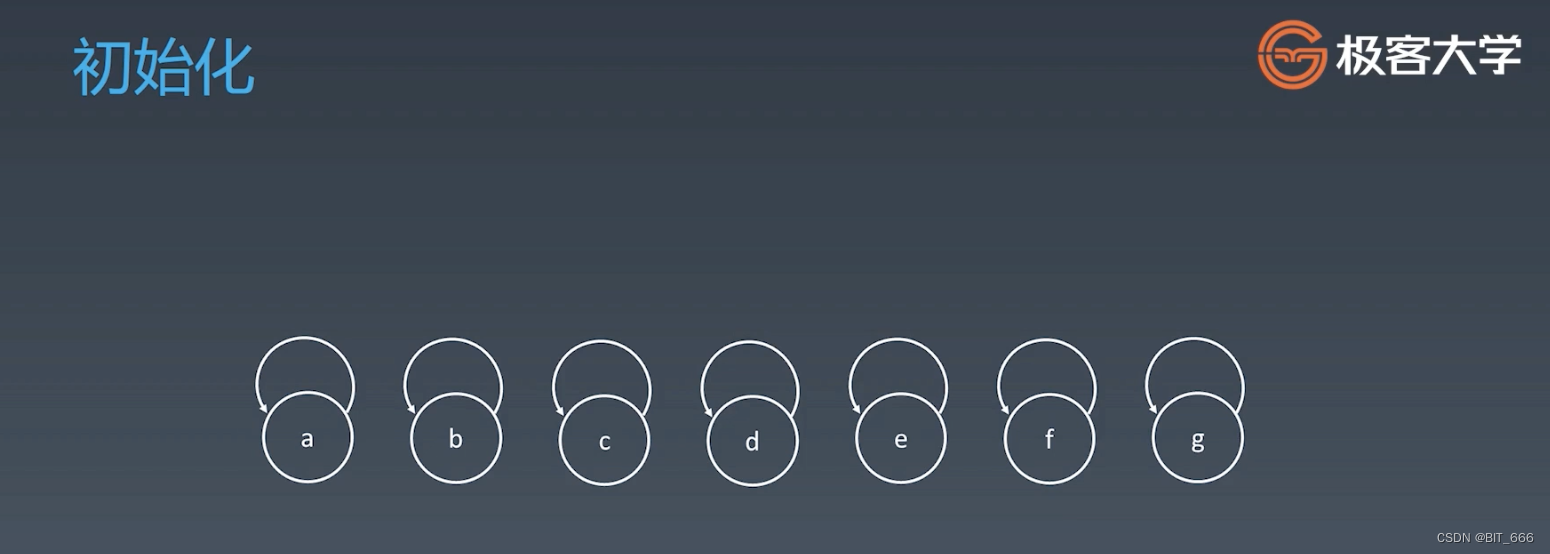
初始化时每一个元素都有一个指针指向自己,指向自己表示自己就是自己的集合。
◆ 查询、合并
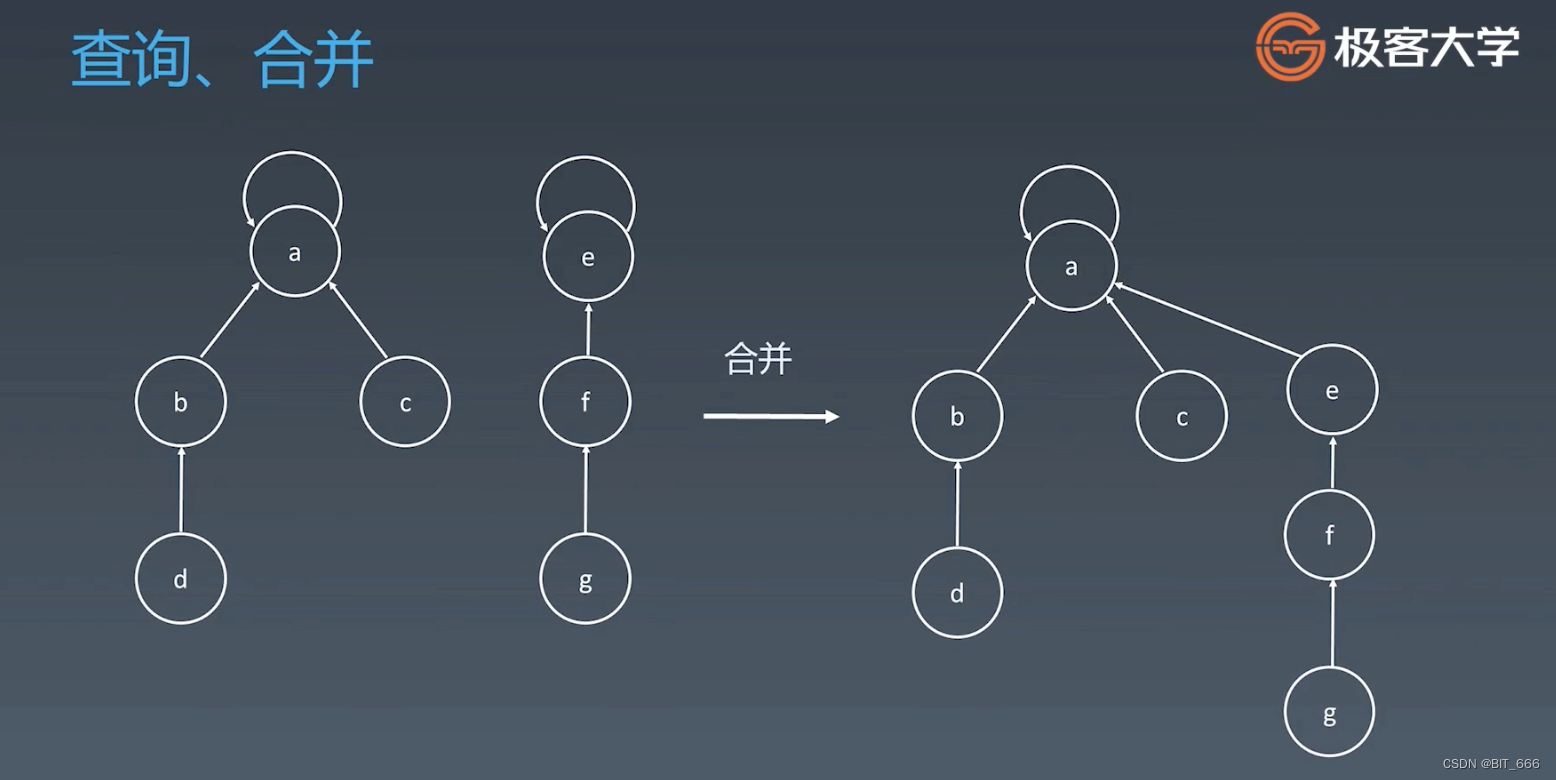
查询 - 查询的话就是一直向上找 parent,直到 parent 等于其自己,说明找到了领头元素。
合并 - a 和 e 代表两个集群,合并时将 a.parent -> e 或者 e.parent -> a
◆ 路径压缩

对于左边的数据结构,d -?c -?b -?a,我们可以修改数据结构,dcb 的 parent 都指向 a,可以减少群组搜索的路径。
3.代码实现

上图给出了 Python 和 Java 的代码实现,第一眼看会感觉字母我都认识,但是逻辑很乱,下面我们基于 Python 代码给大家做一下示例,理解一下。
class bcSet:
"""
# Disjoint-set
"""
p = None
def __init__(self, n):
self.p = [i for i in range(n)]
def union(self, i, j):
p1 = self.parent(i)
p2 = self.parent(j)
self.p[p1] = p2
def parent(self, i):
root = i
# 父节点非自身
while self.p[root] != root:
# 向上找父节点
root = self.p[root]
# 此时 root 为本群老大
while self.p[i] != i:
# 存储临时变量
x = i
# i 指向 i 的父节点
i = self.p[i]
# 路径压缩
self.p[x] = root
return root- init 初始化
根据社群的数量构建数组即可,这里初始化状态为 1:1,即自己以自己为中心的社群。
bc = bcSet(10)
p -> [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]- Union 合并
这里合并的两个节点可以 A -> B,也可以 B -> A,这里是前者,我们合并两个元素。这里我们把 3 -> 4,4 -> 5,可以看到 A -> B 的操作其实就是?A 的索引处修改为 B,即它的父节点索引。p[3] = 4,说明 3 的父节点是 4,p[4] = 5 说明 4 的父节点是 5,所以上面两次合并有?A -> B -> C 的传递关系,类似朋友圈,而圈里的大佬就是 5,因为 p[5] = 5。
bc.union(3, 4)
p -> [0, 1, 2, 4, 4, 5, 6, 7, 8, 9]
bc.union(4, 5)
p -> [0, 1, 2, 4, 5, 5, 6, 7, 8, 9]- Parent 获取父节点
3 -> 4 -> 5 所以向上寻找时二者都属于 5 这个社群,为了优化查询次数上面提到了路径压缩,对应代码的第二个 while 逻辑,第一个 while 循环找到了 root,第二个 while 循环则是遍历社群路径上所有的 i,将其值设置为 root。调用 parent(4) 时不会触发路径压缩,调用 parent(3)?时触发,此时 3、4 的 value 都设置为其父节点 5,即 5/5/5 而不是 4/5/5。
print(bc.parent(4)) -> 5
print(bc.parent(3)) -> 5
p -> [0, 1, 2, 5, 5, 5, 6, 7, 8, 9]三.经典算法实战
1.Friend-Circles
朋友圈:?https://leetcode-cn.com/problems/friend-circles

◆ 题目分析
这里相互认识的同学会在 NxN 的矩阵上体现为互相相连,而没有朋友的点则是一座孤岛,因此其和前面介绍过的岛屿问题很像,不过其在岛屿上不一定是连接的。
◆ DFS 实现
class Solution(object):
def findCircleNum(self, M):
visited = [False] * len(M)
res = 0
def dfs(i):
for j in range(len(M)):
if M[i][j] == 1 and not visited[j]:
visited[j] = True
# 找朋友的朋友
dfs(j)
for i in range(len(M)):
# 第i个朋友还未找朋友
if not visited[i]:
dfs(i)
res += 1
return res
if __name__ == '__main__':
s = Solution()
M = [[1, 1, 0],
[1, 1, 0],
[0, 0, 1]]
print(s.findCircleNum(M))
◆ 并查集实现
class Solution(object):
def findCircleNum(self, M):
if not M:
return 0
# 构建并查集
N = len(M)
bc = bcSet(N)
# 朋友合并在一起
for i in range(N):
for j in range(N):
if i != j and M[i][j] == 1:
bc.union(i, j)
# 找社群大佬数量
return len(set(bc.p))直接套用 bcSet 的 union 方法即可。
2.Num-Of-Island [200]
岛屿数量:?https://leetcode.cn/problems/number-of-islands/

◆ 题目分析
◆ DFS 实现
class Solution(object):
def numIslands(self, grid):
"""
:type grid: List[List[str]]
:rtype: int
"""
# 异常情况
if not grid:
return 0
# 记录岛屿数量
count = 0
# 遍历岛屿
for row in range(len(grid)):
for col in range(len(grid[0])):
if grid[row][col] == "1":
# 沿 (row, col) 递归遍历上下左右
self.dfs(grid, row, col)
count += 1
return count
def inArea(self, grid, row, col):
return 0 <= row < len(grid) and 0 <= col < len(grid[0])
def dfs(self, grid, row, col):
# 不在网格 -> 返回
if not self.inArea(grid, row, col):
return
# 不是岛屿->返回
if grid[row][col] != "1":
return
# 已遍历标记
grid[row][col] = "2"
self.dfs(grid, row - 1, col) # 上
self.dfs(grid, row + 1, col) # 下
self.dfs(grid, row, col - 1) # 左
self.dfs(grid, row, col + 1) # 右每次遍历把能连接的地方标记即可。?
◆ 并查集实现?
class bcSet:
"""
# Disjoint-set
"""
p = None
def __init__(self, n):
self.p = [i for i in range(n)]
def union(self, i, j):
p1 = self.parent(i)
p2 = self.parent(j)
self.p[p1] = p2
def parent(self, i):
root = i
# 父节点非自身
while self.p[root] != root:
# 向上找父节点
root = self.p[root]
# 此时 root 为本群老大
while self.p[i] != i:
# 存储临时变量
x = i
# i 指向 i 的父节点
i = self.p[i]
# 路径压缩
self.p[x] = root
return root
class Solution(object):
def numIslands(self, grid):
M, N = len(grid), len(grid[0])
bc = bcSet(M * N)
sea_count = 0
has_parent = set()
for i in range(M):
for j in range(N):
cur_val = grid[i][j]
if cur_val == "0":
sea_count += 1
elif cur_val == "1":
parent = N * i + j
grid[i][j] == "0"
# 向右、向下
for row, col in ((i, j + 1), (i + 1, j)):
if 0 <= row < M and 0 <= col < N and grid[row][col] == "1":
group = N * row + col
bc.union(group, parent)
# 防止拐弯的情况发生 grid = [["1", "0", "1", "1", "1"], ["1", "0", "1", "0", "1"], ["1", "1", "1", "0", "1"]]
for i in range(len(bc.p)):
if bc.p[i] != bc.parent(i):
bc.p[i] = bc.parent(i)
group = len(set(bc.p))
return group - sea_count
将陆地部分不断融合,并记录海洋的面积,最后把总圈数减去海洋数就是岛屿的数量。这里最后一层 for 循环是防止节点与父节点不一致的情况,又做了一次统一的处理,这里不太容易想到,需要结合实例测试才能发现问题。
3.Surrounded-Regions [130]
被围绕的区域:?https://leetcode.cn/problems/surrounded-regions/description/
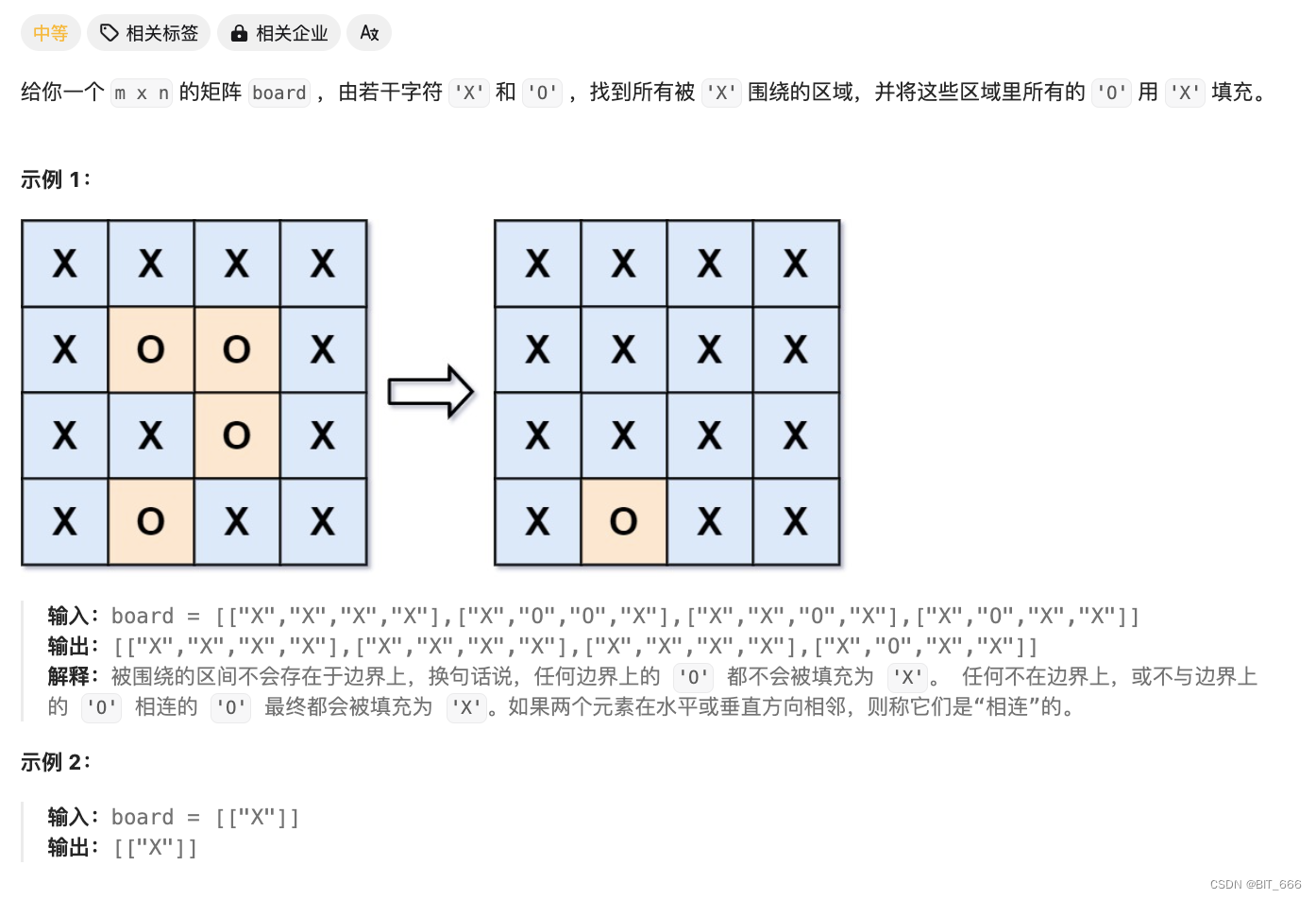
◆ 题目分析
在区域内的 O 我们需要先排除和边界 O 相连的 O,剩下边界内的 O 都修改为 X 即可。首先处理边界的 O,随后遍历整个 Board。
◆ DFS
class Solution(object):
def solve(self, board):
"""
:type board: List[List[str]]
:rtype: None Do not return anything, modify board in-place instead.
"""
if not board or not board[0]:
return
M, N = len(board), len(board[0])
def dfs(row, col):
board[row][col] = "B"
for r, c in ((row + 1, col), (row - 1, col), (row, col + 1), (row, col - 1)):
if 1 <= r < M and 1 <= c < N and board[r][c] == "O":
dfs(r, c)
for j in range(N):
# 第一行
if board[0][j] == "O":
dfs(0, j)
# 最后一行
if board[M - 1][j] == "O":
dfs(M - 1, j)
for i in range(M):
# 第一列
if board[i][0] == "O":
dfs(i, 0)
# 最后一列
if board[i][N - 1] == "O":
dfs(i, N - 1)
# 联通完了,把 O->X 把 B -> O
for i in range(M):
for j in range(N):
if board[i][j] == "O":
board[i][j] = "X"
if board[i][j] == "B":
board[i][j] = "O"
return board
◆ BFS
class Solution:
def solve(self, board):
"""
Do not return anything, modify board in-place instead.
"""
if not board or not board[0]:
return
row = len(board)
col = len(board[0])
def bfs(i, j):
stack = [(i, j)]
while stack:
i, j = stack.pop(0)
if 0 <= i < row and 0 <= j < col and board[i][j] == "O":
board[i][j] = "B"
for x, y in [(-1, 0), (1, 0), (0, -1), (0, 1)]:
stack.append((i + x, j + y))
for j in range(col):
# 第一行
if board[0][j] == "O":
bfs(0, j)
# 最后一行
if board[row - 1][j] == "O":
bfs(row - 1, j)
for i in range(row):
if board[i][0] == "O":
bfs(i, 0)
if board[i][col - 1] == "O":
bfs(i, col - 1)
for i in range(row):
for j in range(col):
if board[i][j] == "O":
board[i][j] = "X"
if board[i][j] == "B":
board[i][j] = "O"
return board?可以使用 collections.deque 的双端队列,也可以直接 list 代替 stack。
◆ 并差集
class bcSet:
"""
# Disjoint-set
"""
p = None
def __init__(self, n):
self.p = [i for i in range(n)]
def union(self, i, j):
p1 = self.parent(i)
p2 = self.parent(j)
self.p[p1] = p2
def parent(self, i):
root = i
# 父节点非自身
while self.p[root] != root:
# 向上找父节点
root = self.p[root]
# 此时 root 为本群老大
while self.p[i] != i:
# 存储临时变量
x = i
# i 指向 i 的父节点
i = self.p[i]
# 路径压缩
self.p[x] = root
return root
class Solution(object):
def solve(self, grid):
M, N = len(grid), len(grid[0])
bc = bcSet(M * N)
for i in range(M):
for j in range(N):
cur_val = grid[i][j]
parent = N * i + j
# 向右、向下
for row, col in ((i, j + 1), (i + 1, j)):
if 0 <= row < M and 0 <= col < N and grid[row][col] == cur_val:
group = N * row + col
bc.union(group, parent)
board_set = set()
for i in range(M):
for j in range(N):
index = N * i + j
if bc.p[index] != bc.parent(index):
bc.p[index] = bc.parent(index)
# 添加边界的群组标记
if i*j == 0 or i == M-1 or j == N-1:
board_set.add(bc.parent(index))
# 非边界群组修改为 X
for i in range(1, M - 1):
for j in range(1, N - 1):
index = N * i + j
if bc.parent(index) not in board_set:
grid[i][j] = "X"
return grid?- 分群 对于能够联通的部分进行分群,此处共有3个群,parent 为 5、13、14
- 将边界分群的 Parent 添加到 set,添加后边界的 parent 为 set(13, 14)
- 对中间部分的元素遍历,如果 parent 不在上面的 set,说明不与边界联通,修改为 'X'

四.总结?
本文介绍了?并查集 的实现和相关算法例题,在实现上我们看到其和字典树也有一定相似,也是在一层一层的嵌套,好处是这里可以通过路径压缩缩短树的路径。只要通过联通或者群组判断的,我们就可以使用 DFS、BFS 以及 Disjoint-Set,根据题型的不同,选择也有区别,第一题朋友圈就适合并查集快速求解,而后面两题则 DFS、BFS 更加效率。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
