卡尔曼滤波原理

1 卡尔曼滤波原理

??卡尔曼滤波算法作为一种重要的最优估计理论被广泛应用于各种领域。组合导航系统的设计一般都是采用Kalman滤波器，Kalman滤波器最早和最成功的应用实例便是在导航领域。卡尔曼滤波有连续型和离散型两种形式，连续型卡尔曼滤波器常用于卡尔曼滤波的理论性能分析，离散型卡尔曼滤波器可以在数字计算机上直接实现，本文将介绍数字型卡尔曼滤波器的使用。
??假设有一个离散线性系统，k时刻的系统状态X_k受到过程噪声W_k-1驱动；系统的状态方程与量测方程均为系统状态量的线性方程：

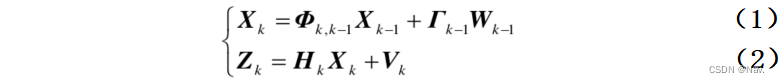
??式中，下标k-1、k分别表示前一时刻 t_k-1 与当前时刻 t_k ，X_k 表示n维状态向量；Φ_k,k?1 为 t_k-1 至 t_k 时刻的状态转移矩阵（n×n）、Γ_k-1 为过程噪声分配矩阵（n×s）、Z_K 为 t_k 时刻的观测向量（m×1）、H_k 为观测矩阵（m×n）；W _k-1 为过程噪声（s×1），V _k 为量测噪声（m×1）。

注意：
??W _k-1 和 V _k 要求是互不相关的零均值的高斯白噪声序列，即满足：

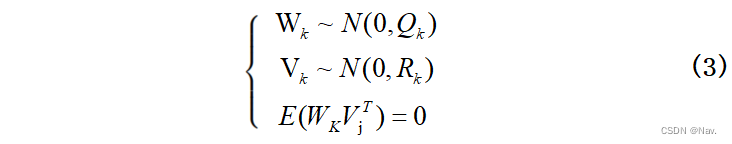
??式中，Q_k 为系统状态噪声方差阵，R_k 为量测噪声方差阵。

??在一个卡尔曼滤波周期内,其过程可以分为时间更新和量测更新。时间更新又称为预测，下述是时间更新计算状态量与协方差矩阵的过程：

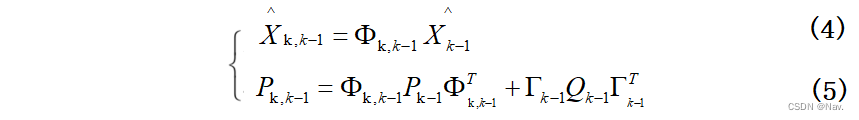
??式中$\hat{X}$_k-1为前一时刻 t_k-1 状态向量的最优估计值，$\hat{X}$_k,k-1 为当前时刻t_k 的状态最优预测值。P_k,k-1 为当前时刻 t_k 的状态最优估计的方差协方差阵的预测值，P_k-1 为前一时刻 t_k-1 的方差协方差阵最优估计值。

??当观测值到来时，我们进行量测更新。在量测更新过程中我们要先计算增益矩阵K，然后更新系统状态X和方差协方差矩阵P。下述为量测更新计算状态量与协方差矩阵的过程：

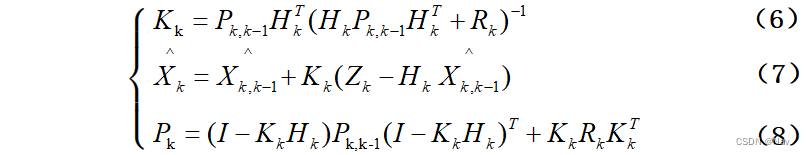
??公式(4)~(8)即卡尔曼滤波器的五个公式，只要给定初值 $\hat{X}$₀ 和P₀ ，根据 t_k 时刻的观测值就可以计算出 t_k 时刻的状态估计 $\hat{X}$_k 。但是要将卡尔曼滤波用于实际模型中却又诸多考量：若系统模型与实际运动模型不匹配，或观测模型与实际观测输出不匹配时，都可能导致滤波发散，得到错误结果。因此在使用卡尔曼滤波时，应优化实际问题的数学模型、合理地设置过程噪声、观测噪声，使状态空间模型尽可能准确才能获取精确的状态估计。

2 卡尔曼滤波器代码实现

function kf = Kfupdate(kf, yk, TimeMeasBoth)
%*************************************************************%
  % @brief  卡尔曼滤波器
  % @param  kf：卡尔曼滤波器参数
  % @param  yk：观测值
  % @param  TimeMeasBoth：判断时间更新还是量测更新参数
  % @retval kf：卡尔曼滤波器参数
  %具体原理参考：https://blog.csdn.net/weixin_47268803/article/details/134949948
%*************************************************************%
    if nargin==1
        TimeMeasBoth = 'T';%时间更新
    elseif nargin==2
        TimeMeasBoth = 'B';%量测更新
    end
    
    if TimeMeasBoth=='T'            % 时间更新
        kf.xk = kf.Phikk_1*kf.xk;  %参考公式（4）
        kf.Pxk = kf.Phikk_1*kf.Pxk*kf.Phikk_1' + kf.Gammak*kf.Qk*kf.Gammak';%参考公式（5）
    else
        if TimeMeasBoth=='M'        % 时间更新
            kf.xkk_1 = kf.xk;    
            kf.Pxkk_1 = kf.Pxk; 
        elseif TimeMeasBoth=='B'    % 时间&量测更新
            kf.xkk_1 = kf.Phikk_1*kf.xk;    
            kf.Pxkk_1 = kf.Phikk_1*kf.Pxk*kf.Phikk_1' + kf.Gammak*kf.Qk*kf.Gammak';
        else
            error('TimeMeasBoth input error!');
        end
        kf.Pxykk_1 = kf.Pxkk_1*kf.Hk';%参考公式（6）：Pk,k-1 * H'
        kf.Py0 = kf.Hk*kf.Pxykk_1;%参考公式（6）：H * Pk,k-1 * H'
        kf.ykk_1 = kf.Hk*kf.xkk_1;%参考公式（7）：H * Xk,k-1
        kf.rk = yk-kf.ykk_1;%参考公式（7）：Zk - H * Xk,k-1

        kf.Pykk_1 = kf.Py0 + kf.Rk;%参考公式（6）：H * Pk,k-1 * H' + Rk
        kf.Kk = kf.Pxykk_1*invbc(kf.Pykk_1); % kf.Kk = kf.Pxykk_1*kf.Pykk_1^-1;参考公式（6）
        
        kf.xk = kf.xkk_1 + kf.Kk*kf.rk;%参考公式（7）
        kf.Pxk = kf.Pxkk_1 - kf.Kk*kf.Pykk_1*kf.Kk';%参考公式（8）和《捷联惯导算法与组合导航原理》P125 （5.3.31b）
        
    end