Python房价分析（三）支持向量机SVM分类模型

目录

1 数据预处理

1.1 房价数据介绍

1.2 数据预处理

2 SVM模型

2.1 模型概述

2.2 核函数选择

2.3 建模步骤

2.4 参数搜索过程

3模型评估

3.1 模型评估结果

3.2 混淆矩阵

3.3 绘制房价类别三分类的ROC曲线和AUC数值

3.4 模型比较

总结

---

往期精彩内容：

房价分析（0）反爬虫机制_python爬取房价数据-CSDN博客

Python房价分析（一）pyton爬虫-CSDN博客

Python房价分析（二）随机森林分类模型-CSDN博客

1 数据预处理

1.1 房价数据介绍

房价数据来源于上期Python爬虫所获取的数据

Python房价分析（一）pyton爬虫-CSDN博客

本文采用宜昌市二手房数据进行讲解，数据如图所示，共3000条样本，有区域、街道、房型、朝向、面积、楼层数、装修类型、房屋结构、收藏数、价格 10个特征。

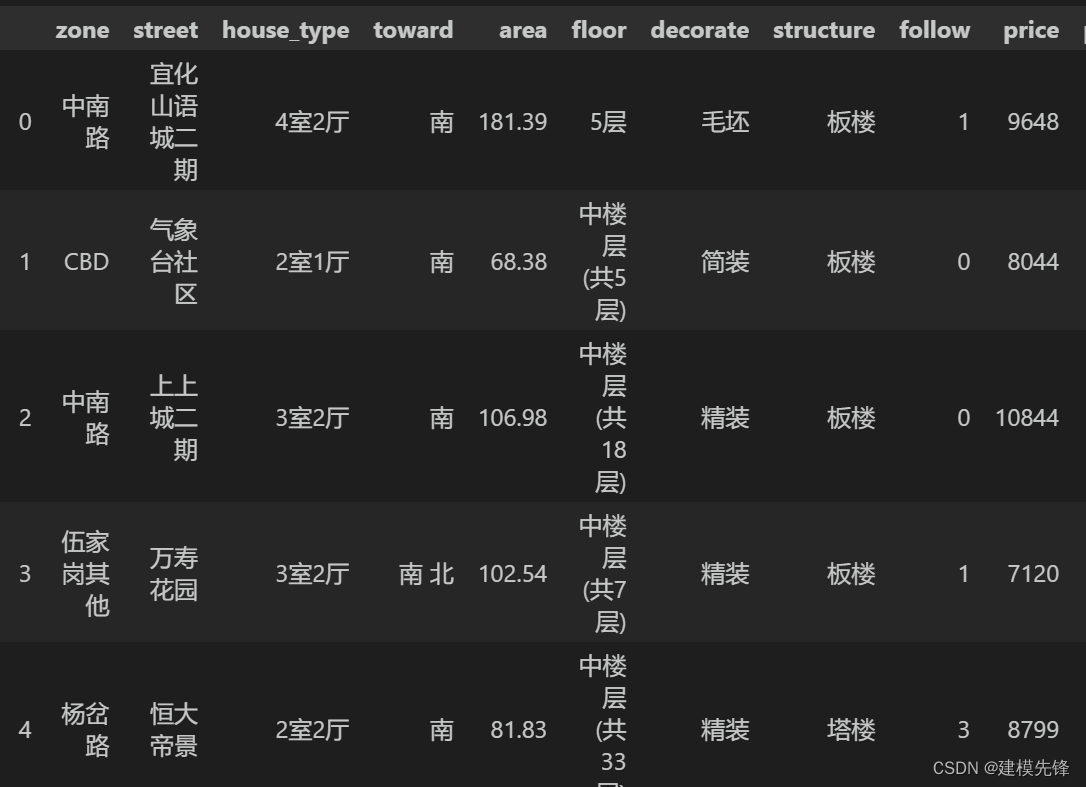
1.2 数据预处理

数据的偏离程度以及数据之间的关联性会拉大整体数据标准差、造成统计偏见以及使数据带有指向性偏好，这都会影响到我们最终模型和分析的结果，造成偏差，可见在进行统计与计算前对数据处理的必要性与重要性。

数据归一化：

由于数据集中大多数特征指标不满足正态分布，不能采用常规的z-score 标准化。而数据集经过异常值处理后，减小了数据归一化受离群点影响，我们采用Min-Max归一化即极差法，将数据集中列数值缩放到0和1之间，来处理量纲的问题。

分类特征编码：

对于数据集中的多分类特征变量，把不能量化的多分类变量量化，使得每个哑变量对模型的影响都细化，从而提高模型精准率。分类变量编码能够加速参数的更新速度；使得一个很大权值管理一个特征，拆分成了许多小的权值管理这个特征多个表示，降低了特征值扰动对模型的影响，模型具有更好的鲁棒性。因此，我们采用OneHot独热编码来为其创建分类类别特征。

2 SVM模型

2.1 模型概述

支持向量机（SVM）是一类按监督学习方式对数据进行二元分类的广义线性分类器，其决策边界是对学习样本求解的最大边距超平面，可以将问题化为一个求解凸二次规划的问题。与逻辑回归和神经网络相比，支持向量机，在学习复杂的非线性方程时提供了一种更为清晰，更加强大的方式。

具体来说就是在线性可分时，在原空间寻找两类样本的最优分类超平面。在线性不可分时，加入松弛变量并通过使用非线性映射将低维度输入空间的样本映射到高维度空间使其变为线性可分，这样就可以在该特征空间中寻找最优分类超平面。

2.2 核函数选择

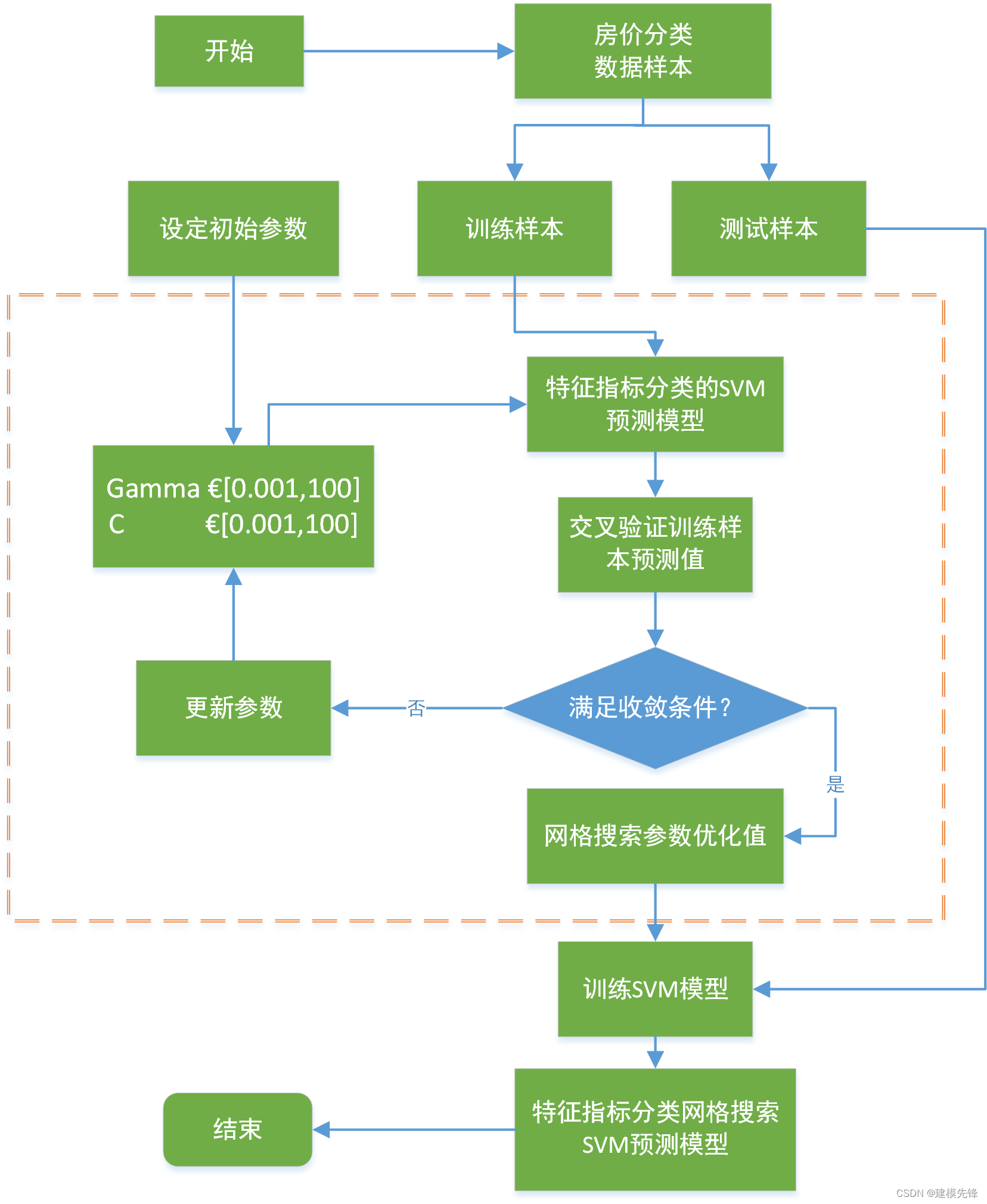
具体选择哪种类型的核函数以及核函数中参数如何选择，应该实验不同的核函数和不同的参数进行组合，网格搜索是最简单、应用最广泛的超参数搜索算法，它通过查找搜索范围内的所有的点来确定最优值[1]。如图所示，为提高搜索效率，本文采用大步长粗搜，小步长精搜的思路寻找所有可能的参数组合。

2.3 建模步骤

Step1.特征变量和目标变量提取，我们分析利用二手房价高、中、低三分类作为目标变量，把区域、街道、楼房名称、户型、朝向、建筑面积、楼层、装修、结构、关注作为特征变量；

Step2.先对特征数据集进行标准化处理，然后进行训练集和测试集数据划分，本文将原始数据集进行分割，将训练集与测试集进行划分，将前70%的数据作为训练集，后30%的数据作为测试集；

导入相关包

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split,GridSearchCV,cross_val_score
from sklearn.metrics import confusion_matrix, accuracy_score,classification_report
from sklearn import preprocessing
from sklearn import svm
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rc("font", family='Microsoft YaHei')

读取 预处理后的 数据

# 读取 预处理后的 数据
price_classify_data = pd.read_csv('yichang_deal.csv')
X = price_classify_data[['zone_label','street_label','type_label','toward_label','area','floor_label',
                         'decorate_label','structure_label','follow']]

Y = price_classify_data['price_label']
# 标准化
X = preprocessing.scale(X)
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.3, random_state=200)  # 随机数种子

Step3.利用Python的开源机器学习库scikit-learn构建分类模型，采用支持向量机分类方法进行建模。利用管道对模型进行复合调参，网格搜索是最简单、应用最广泛的超参数搜索算法，它通过查找搜索范围内的所有的点来确定最优值。

2.4 参数搜索过程

参数介绍

• C:正则化参数。正则化的强度与C成反比。必须严格为正。惩罚是平方的l2惩罚。
• kernel:{'linear','poly','rbf','sigmoid','precomputed'}，默认='rbf'
• degree:多项式和的阶数
• gamma:“ rbf”,“ poly”和“ Sigmoid”的内核系数。shrinking:是否软间隔分类,默认true
• decision_function_shape：分类形式（二分类或多分类）

kernel='linear'时,为线性核,C越大分类效果越好,但有可能会过拟合(defaul C=1)。

kernel='rbf'时(defaul),为高斯核,gamma值越小,分类界面越连续;gamma值越大,分类界面越“散”,分类效果越好,但有可能会过拟合。

decision_function_shape='ovr'时,为one v rest,即一个类别与其他类别进行划分,decision_function_shape='ovo'时,为one v one,即将类别两两之间进行划分,用二分类的方法模拟多分类的结果。

参数网格搜索：

# 复合调参
from sklearn.pipeline import Pipeline
from sklearn.feature_selection import SelectKBest, chi2, f_classif
from sklearn.model_selection import GridSearchCV
pipe = Pipeline([
    ('selector', SelectKBest()),       # 特征选择
    ('model', svm.SVC(random_state=200))  # 模型
])

# 参数
parameters = [
    {
        # 'selector__score_func': [chi2, f_classif],
        'kernel':['linear'],
        'C':[0.1, 1, 10,100],
        'decision_function_shape':['ovo']
    },
    {
        'kernel': ['poly'],
        'coef0':[0.1,1,10],
        'degree':[1, 3, 5],
        'C':[0.1, 1, 10,100],
        'gamma': [0.1,1,10,100],
        'decision_function_shape':['ovo']
    },
    {
        'kernel':['rbf'],
        'gamma': [0.1,1,10,100],
        'C':[0.1, 1, 10,100],
        'decision_function_shape':['ovo']
    },
    {
        'kernel':['sigmoid'],
        'gamma': [0.1,1,10,100],
        'coef0':[0.1,1,10],
        'C':[0.1, 1, 10,100],
        'decision_function_shape':['ovo']
    }
]
train_model =svm.SVC() # 构建分类器
gird_search = GridSearchCV(
    pipe,
    parameters,
    cv=10,
    scoring='accuracy'
)

gird_search.fit(X_train, Y_train)
# 最优参数结果
print(gird_search.best_score_)
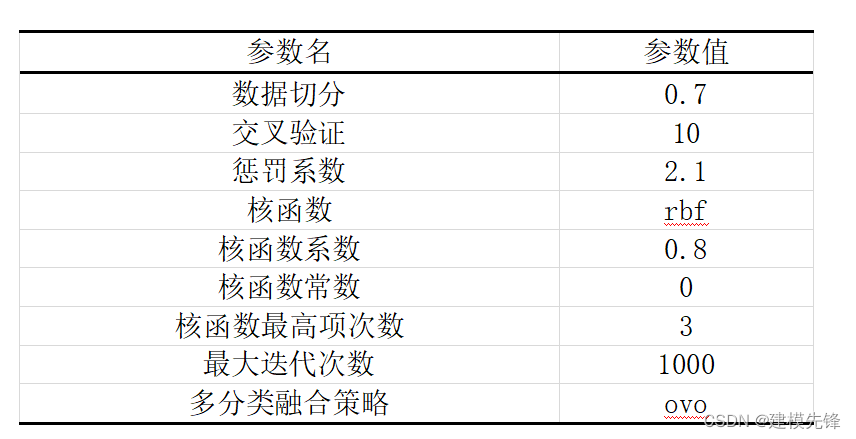
print(gird_search.best_params_)

通过网格搜索，设置模型参数如表8所示：采用10折交叉验证，惩罚系数设置为2.1，核函数设置为高斯核函数，核函数系数为0.8，最大迭代次数为1000，多分类融合策略为ovo。

3模型评估

3.1 模型评估结果

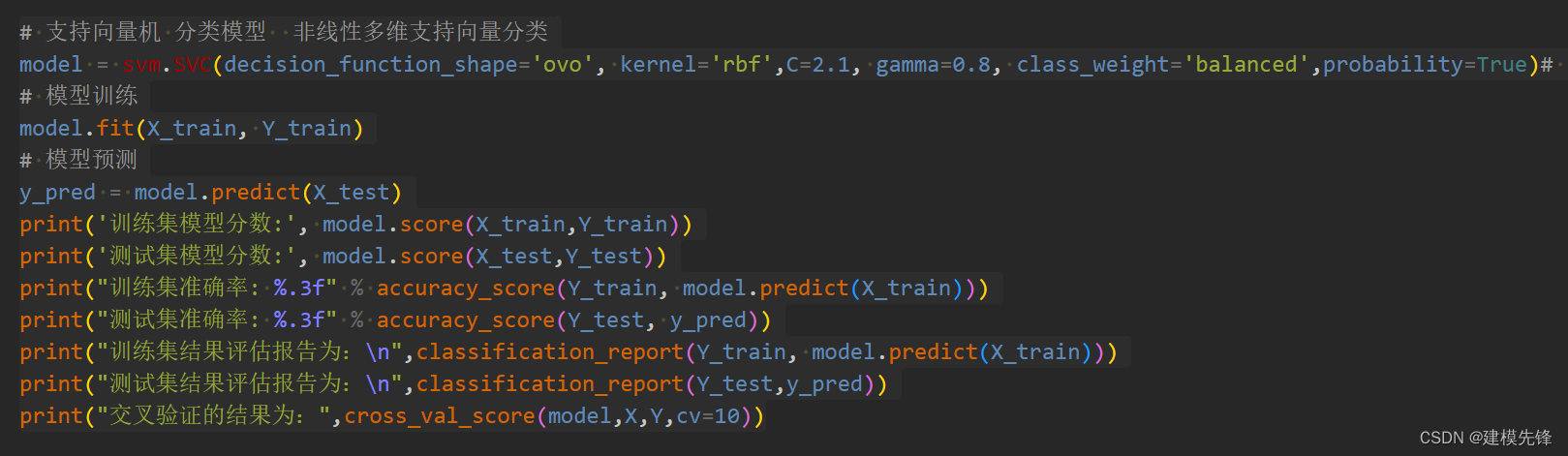
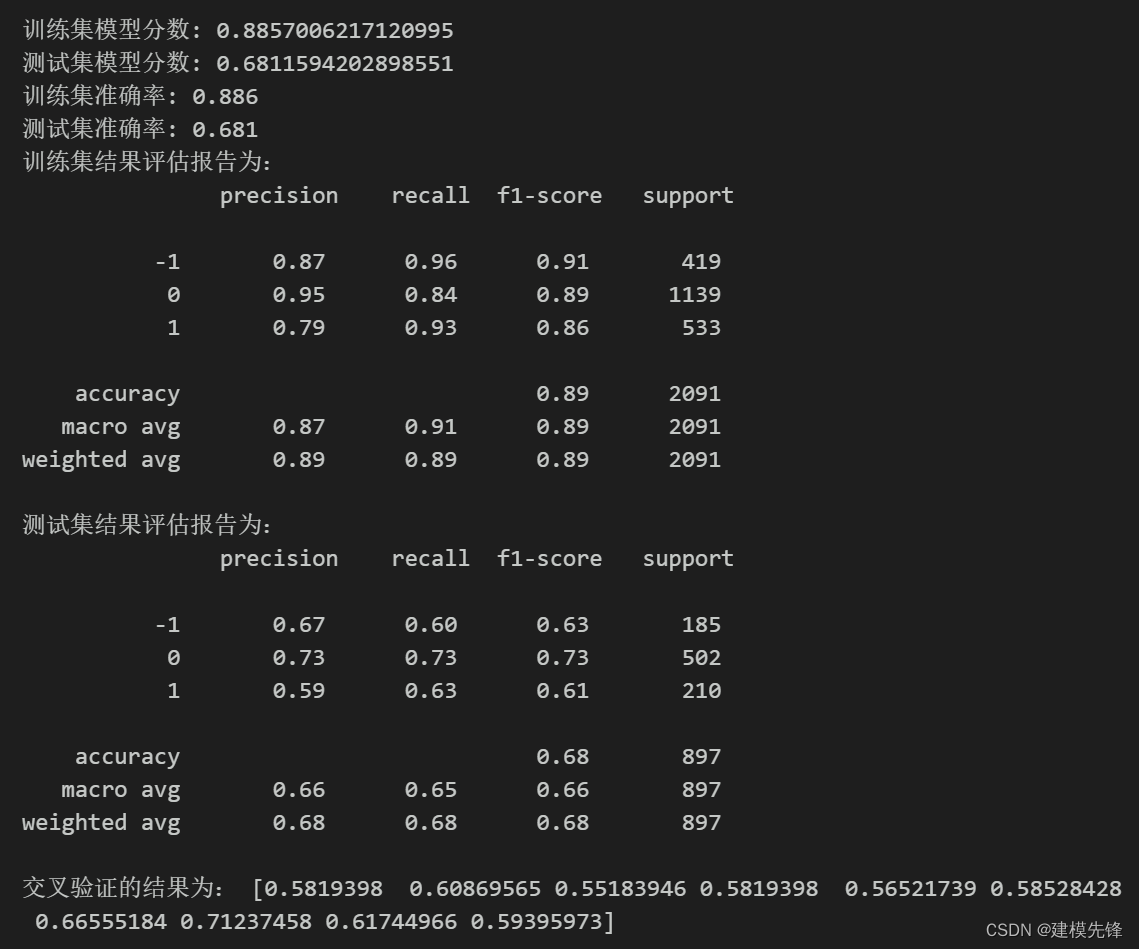
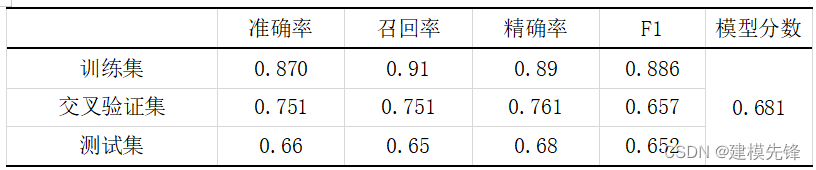
模型评估结果如表所示，表中展示了训练集和测试集的分类评价指标，通过量化指标来衡量随机森林对训练、测试数据的分类效果。准确率：预测正确样本占总样本的比例，准确率越大越好；召回率：实际为正样本的结果中，预测为正样本的比例，召回率越大越好；精确率：预测出来为正样本的结果中，实际为正样本的比例，精确率越大越好；F1：精确率和召回率的调和平均，精确率和召回率是互相影响的，虽然两者都高是一种期望的理想情况，然而实际中常常是精确率高、召回率就低，或者召回率低、但精确率高。若需要兼顾两者，那么就可以用F1指标。支持向量机的精确率表现一般，其模型分数在测试集结果为0.681.

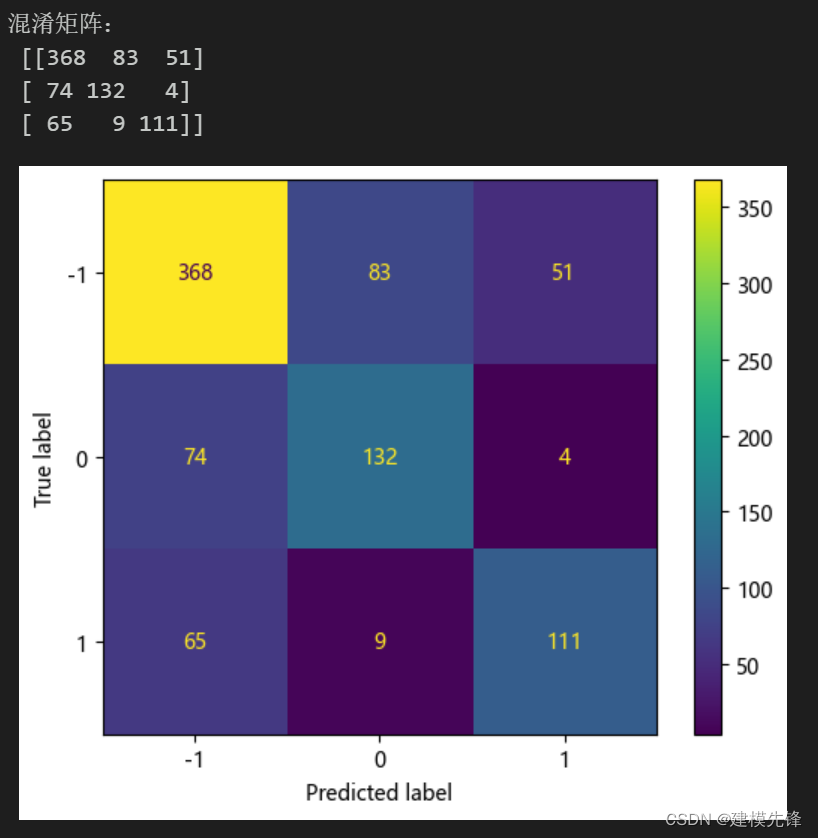
3.2 混淆矩阵

# 混淆矩阵
from sklearn.metrics import confusion_matrix
import matplotlib.ticker as ticker

cm = confusion_matrix(Y_test, y_pred,labels=[0,1,-1])
print('混淆矩阵：\n', cm)
labels=['-1','0','1']
from sklearn.metrics import ConfusionMatrixDisplay
cm_display = ConfusionMatrixDisplay(cm,display_labels=labels).plot()

以热力图的形式展示了SVM分类模型结果的混淆矩阵

3.3 绘制房价类别三分类的ROC曲线和AUC数值

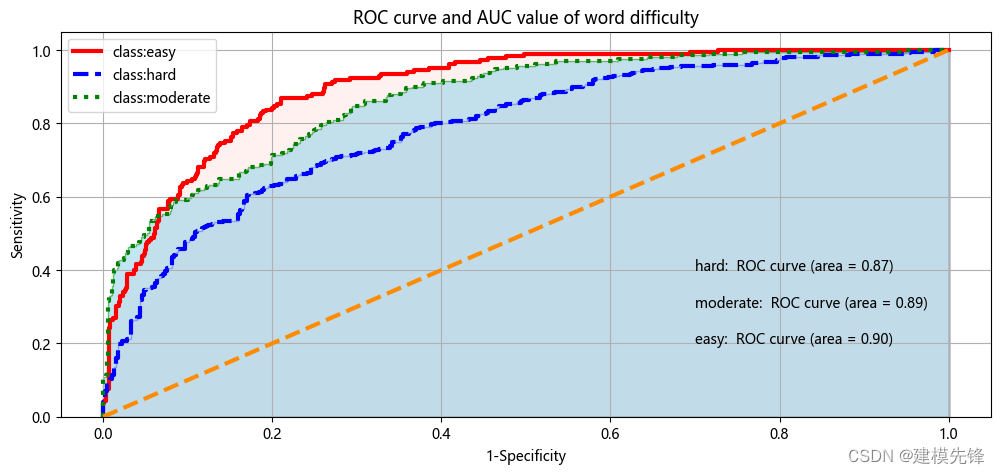
模型ROC曲线和AUC数值如图所示，图中的橙色线为参考,即在不使用模型的情况下,Sensitivity 和1-Specificity之比恒等于1。通过绘制ROC曲线,重要的是计算折线下的面积,即图中的阴影部分,这个面积称为AUC。在做模型评估时,希望AUC的值越大越好,通常情况下,当AUC在0.8以上时,模型就基本可以接受了。在AUC>0.5的情况下，AUC越接近于1，说明模型效果越好；AUC在 0.5~0.7时有较低准确性，AUC在0.7~0.9时有一定准确性，AUC在0.9以上时有较高准确性；AUC=0.5时，跟随机猜测一样，模型没有分类价值；AUC<0.5时，比随机猜测还差。然而支持向量机分类模型三种分类的AUC值分别为0.87、0.79、0.90,说明模型分类效果比较明显。

3.4 模型比较

结合上期随机森林模型，根据宜昌市二手房的数据集训练结果看，模型比较如表所示，随机森林分类模型从准确率均值、召回率均值、精确率均值、F1均值、AUC均值、模型分数都要比支持向量机分类模型效果要好的多，在此数据集上，使用随机森林分类模型效果会明显一点。

总结

支持向量机优点：由于采用核函数方法克服了维数灾难和非线性可分的问题，所以向高维空间映射时没有增加计算的复杂性。换句话说，由于支持向量计算法的最终决策函数只由少数的支持向量所确定，所以计算的复杂性取决于支持向量的数目，而不是样本空间的维数；SVM的处理方法是只考虑support vectors，也就是和分类最相关的少数点，去学习分类器。

支持向量机缺点：经典的支持向量机算法只给出了二分类的算法，而在实际应用中，一般要解决多分类问题，但支持向量机对于多分类问题解决效果并不理想；SVM算法效果与核函数的选择关系很大，往往需要尝试多种核函数，即使选择了效果比较好的高斯核函数，也要调参选择恰当的参数。

每种算法都有其各自的优点和使用场景，没有最好的算法，只有更好的数据。

参考资料

[1]田芳,周孝信,于之虹. 基于支持向量机综合分类模型和关键样本集的电力系统暂态稳定评估[J]. 电力系统保护与控制,2017,45(22):1-8. DOI:10.7667/PSPC161864.