动态规划中的状态转移方程和最优子结构
LeetCode 64:给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。说明:每次只能向下或者向右移动一步。
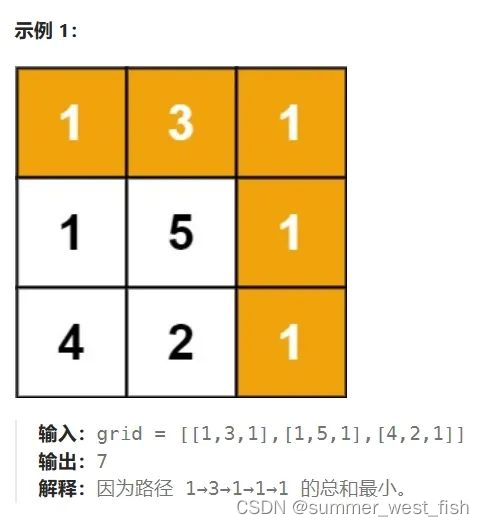
这个问题的本质其实是一个背包问题。
把 i 设置为向下走,把 j 设置为向右走,从 (0,0) 走到 (i,j) 的最小路径总和置为f[i][j]。那么我们是怎么走到(i,j)的呢?有三种可能。
-
当前位置只能通过往下移动而来,即有f[i][j] = f[i-1][j] + grid[i][j]
-
当前位置只能通过往右移动而来,即有f[i][j] = f[i][j-1] + grid[i][j]
-
当前位置既能通过往下也能往右移动,为了使路径上的数字总和为最小,需要在向下和向右走之前取一个最小值,既有f[i][j] = min(f[i][j-1],f[i-1][j]) + grid[i][j]
像这样,当前阶段的状态往往是上一阶段状态和相应决策的结果,采用指标函数来表示它们之间的关系称为状态转移方程。?
?代码实现:
public static int minPathSum(int[][] grid) {
int m = grid.length, n = grid[0].length;
int[][] f = new int[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (i == 0 && j == 0) {
f[i][j] = grid[i][j];
} else {
//如果是第一行或第一列只需要考虑left或者top值
//其余位置则需要选取left和top比较后较小的值
int top = i - 1 >= 0 ? f[i - 1][j] + grid[i][j] : Integer.MAX_VALUE;
int left = j - 1 >= 0 ? f[i][j - 1] + grid[i][j] : Integer.MAX_VALUE;
f[i][j] = Math.min(top, left);
}
}
}
return f[m - 1][n - 1];
}这道题中,有一个最小路径总和,也就是有一个最优解。像这样,我们可以通过计算子问题的最优解可以来构建整个问题的最优解,我们就说这个问题具有最优子结构,即满足最优性原理。
你甚至不需要看懂这道题答案的具体代码,只需要你能理解啥是状态转移方程和最优子结构。
?
能采用动态规划求解的问题的一般要具有以下性质:
-
具有最优子结构:如果问题的最优解所包含的子问题的解也是最优的,就称该问题具有最优子结构,即满足最优性原理。
-
有重叠子问题:即子问题之间是不独立的,一个子问题在下一阶段决策中可能被多次使用到。
?
总结出动态规划法在实际应用中简化的步骤:
-
分析最优解的性质,并刻画其结构特征
-
递归的定义最优解,得到状态转移方程/递推关系式【难点】
-
以自底向上方式计算出最优值【填表】
-
根据计算最优值时得到的信息,构造问题的最优解【可选】,这里的第四步,构造问题的最优解,不是必须的,但是有一些题目需要。
动态规划法是一种用空间换时间的技术,本质上是一种比较 “聪明” 的枚举法。
?
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!