数据结构——栈
目录
栈是一种常用而且重要的数据结构之一,如用于保存函数调用时所需要的信息,通常再将递归算法转换成非递归算法时需要使用到栈。很多编辑器的撤销操作以及括号匹配等等都是使用栈来实现。
一、栈的定义
栈是一种只能在一端进行插入或删除操作的线性表。表中允许进行插入、删除操作的一端称为栈顶,表的另一端称为栈底。如下图所示。

在栈中,栈顶的位置是动态变化的,它会根据出栈和进栈操作变更栈顶的位置,进栈操作是将一个元素插入到栈中(只能插入到栈顶),出栈操作是将栈顶元素从栈中删除。进栈操作后栈顶的位置将会变为插入元素所在的位置,出栈操作后栈顶的位置将会变为原栈顶元素的上一个元素的位置。
栈顶的位置通常用一个指向栈顶元素的指针或者索引来表示,执行进栈和出栈操作后只需要更改对于的栈顶索引或者指针即可。
进栈操作如下图:

插入元素后,栈顶位置对应移动到插入元素的位置?
出栈操作如下图:
?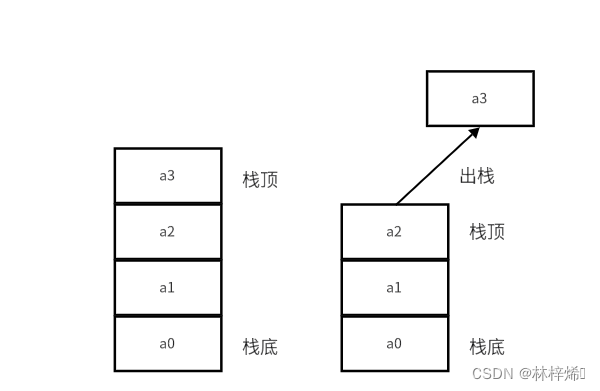
删除元素后,栈顶位置对应移到到上一个元素的位置。?
由于栈的特殊性,它的基本操作都只能在栈顶进行,?因此它的实现比较简单。栈的基本操作包括:插入元素,删除元素,查询元素,判断非空等,其中前三个操作都只能在栈顶出进行。、
二、栈的存储
栈有两种存储方式:顺序存储和链式存储。顺序存储就是用顺序表存储栈,以顺序表末尾的元素的索引作为栈顶的位置。链式存储是用链表存储栈,以链表的操作来执行进栈出栈操作。这里我只实现了栈的顺序存储,栈的链式存储和顺序存储只差在存储结构不同,将对应的操作改为链表的操作即可。
1. 栈类的定义
template<typename T>
class MyStack
{
private:
T* data; // 栈的存储数组(数组变量就是指针,未初始的时候不能用data[])
int topIndex; // 栈顶的索引
int size; // 栈的长度
public:
MyStack();
~MyStack();
bool empty();
bool push(T value);
bool pop();
T top();
int getSize();
};如上述代码,栈类包括三个数据成员:存储数组data、栈顶索引topIndex、栈的大小size,成员函数包括:创建栈MyStack()、销毁栈~Mystack()、判断栈是否为空empty()、进栈push()、出栈pop()、取栈顶元素top()以及获取栈大小getSize()。
现在一一实现上面的各个操作函数。
1. 创建栈
创建栈有两个构造函数可选,一个无参构造,直接创建一个空的栈,为数据成员初始化,申请data数组存储空间(大小默认为宏定义MAXSIZE),初始化top索引以及栈大小。另一个有参构造可以传入一个包含数组的数组以及数组中可用数据的长度,使用该数组作为栈的存储数组。
// 初始化栈,无参构造,创建一个空栈
MyStack() {
data = new T[MAXSIZE];
topIndex = -1;
size = 0;
}
// 有参构造,以一个数组构造一个栈,n为数组长度
MyStack(T data[], int n) {
this.data = data;
topIndex = n - 1;
size = 0;
}2. 销毁栈?
当栈类不再使用后,系统调用析构函数销毁栈类,析构函数需要做的操作是将data数组的空间释放,并将topIndex和size的值改为初始值,这个操作也可以不做。
~MyStack() {
delete[] data;
topIndex = -1;
size = 0;
}3. 进栈
进栈操作对于顺序表存储的栈只需要将栈顶元素的下一个元素赋值为要插入的元素即可,并且同步更新topIndex和size的值。注意需要判断此时栈是否是满的(超过data数组的上限),如果是满的则返回插入失败。
bool push(T value) {
// 超过栈能存储的上限,栈已满
if (topIndex == MAXSIZE - 1) {
return false;
}
// 插入元素
data[++topIndex] = value;
size++;
return true;
}4. 出栈
出栈操作只需要将栈顶索引减一,使其指向原本栈顶元素的上一个元素并同步更新size的值,不需要直接删除数组中栈顶的元素,因为用户不能直接访问data数组,只能根据top访问对应的元素。
bool pop() {
if (empty()) {
return false;
}
topIndex--;
size--;
return true;
}5. 取栈顶元素
直接使用topIndex索引访问对应栈顶元素,返回即可。
T top() {
if (empty()) {
throw out_of_range("栈为空,无法访问栈顶元素");
}
return data[topIndex];
}6. 栈是否为空?
栈顶的索引是从0开始的,因此初始将栈顶索引设为-1,表示栈为空,所以要判断栈是否为空只需要判断栈顶索引是否为-1即可。
bool empty() {
return topIndex == -1;
}测试:
MyStack<string> st;
cout << "栈是否为空:" << st.empty() << "\t栈长度:" << st.getSize() << endl;
cout << "插入元素'lin'" << endl;
st.push("lin");
cout << "栈是否为空:" << st.empty() << "\t栈长度:" << st.getSize() << endl;
cout << "插入元素'zixi'" << endl;
st.push("zixi");
cout << "栈是否为空:" << st.empty() << "\t栈长度:" << st.getSize() << endl;
if (!st.empty())
cout << "栈顶元素:" << st.top() << endl;
cout << "弹出元素" << endl;
st.pop();
cout << "栈是否为空:" << st.empty() << "\t栈长度:" << st.getSize() << endl;
if (!st.empty())
cout << "栈顶元素:" << st.top() << endl;
cout << "弹出元素" << endl;
st.pop();
cout << "栈是否为空:" << st.empty() << "\t栈长度:" << st.getSize() << endl; 测试结果:?

测试结果全部正确。
c++中是有现成的栈类的,类名是stack,包含在头文件stack中。
三、栈的应用
栈的一个经典的应用就是中缀表达式转换后缀表达式以及后缀表达式计算。现在我们使用自己定义的栈来解决这个问题。
1. 表达式转换
问题描述:
给出一个中缀表达式字符串,将其转换为后缀表达式,并计算结果。
比如将中缀表达式1+3*2/4转换为1 3 2 * 4 / +,计算结果为2.5。
解决过程:
中缀表达式就是我们平常使用的计算式,根据符号的优先级来计算,而后缀表达式不需要考虑优先级,按每次取两个操作数计算得到最终结果。
中缀表达式转换为后缀表达式的过程如下:
1. 遍历中缀表达式字符串
? ? ? ? 1.1. 如果当前字符是左括号 '(':
? ? ? ? ? ? ? ? 1.1.1. 直接入栈;
? ? ? ? 1.2. 如果当前字符是右括号 ')':
? ? ? ? ? ? ? ? 1.2.1. 将栈中元素依次弹出,直到遇到左括号(左括号也要弹出);
? ? ? ? 1.3. 如果当前字符是乘除号 '*'、'/':
? ? ? ? ? ? ? ? 1.3.1. 将栈中元素依次弹出直到遇到运算优先级比自己低的符号为止('+'、'-'、‘(’);
? ? ? ? ? ? ? ? 1.3.2. 将弹出的元素依次加入到后缀表达式postExpr中;
? ? ? ? ? ? ? ? 1.3.3. 将当前字符入栈;
? ? ? ? 1.4. 如果当前字符是加减号 '+'、'-':
? ? ? ? ? ? ? ? 1.4.1. 如果当前字符是加减号,则将栈中元素依次弹出直到遇到优先级比自己低的符号为止('(');
? ? ? ? ? ? ? ? ????????1.4.1.1.?将弹出的元素依次加入到后缀表达式postExpr中;
? ? ? ? ? ? ? ? ????????1.4.1.2.?将当前字符入栈;
? ? ? ? ? ? ? ? 1.4.2. 如果当前字符是操作数的正负号,则直接将当前字符加入postExpr中,不入栈;
? ? ? ? 1.5. 如果当前字符是操作数:
? ? ? ? ? ? ? ? 1.5.1. 将连续的操作数(操作数可能有多位)直接添加进postExpr中,不入栈;
2. 如果栈中还存在操作符:
? ? ? ? 2.1. 将栈中操作符依次弹出并添加进postExpr中;
3. 返回后缀表达式postExpr;
具体原理是什么我忘了,但是操作步骤大概就是这样。
一个简单的流程示例:

对应代码:
// 转换表达式,中缀表达式转化为后缀表达式
string cvrtExpr(string expr) {
string rsExpr;
// 存储符号的栈,操作数不入栈
MyStack<char> opSt;
// 存储后缀表达式字符串
string postExpr = "";
for (int i = 0; i < expr.length(); i++) {
char c = expr[i];
// 遇到左括号直接进栈
if (c == '(') {
opSt.push(c);
}
// 遇到右括号全部出栈直到遇到左括号
else if (c == ')') {
while (!opSt.empty() && opSt.top() != '(') {
// 将操作符加入后缀表达式中,以空格间隔
// 字符串和字符之间不能直接用+加起来,将字符和空格分开加入postExpr
postExpr += opSt.top();
postExpr += " ";
opSt.pop();
}
// 左括号也要出栈
opSt.pop();
}
// 遇到乘除号先将栈内的优先级低的符号出栈再入栈,遇到左括号或者优先级不低于其的符号停止
else if (c == '*' || c == '/') {
while (!opSt.empty() && opSt.top() != '+' && opSt.top() != '-' && opSt.top() != '(') {
postExpr += opSt.top();
postExpr += " ";
opSt.pop();
}
// 将该符号入栈
opSt.push(c);
}
// 加减号需要判断是加减号还是数字的正负号,如果是加减号与乘除法一样的处理步骤
else if (c == '+' || c == '-') {
// 如果是加减号则该运算前面一个字符是数字或者右括号
// 如果是第一个字符那么是正负号(避免访问-1)
//if (i != 0 && (isdigit(expr[i - 1]) || expr[i - 1] == ')') && (isdigit(expr[i + 1])) || expr[i + 1] == '(')
if (!isSign(expr, i)) {
while (!opSt.empty() && opSt.top() != '(') {
postExpr += opSt.top();
postExpr += " ";
opSt.pop();
}
opSt.push(c);
}
// 如果不是加减号,而是正负号,则将其加入后缀表达式中,并且不加空格分隔,作为操作数的一部分
else if (isSign(expr, i))
postExpr += c;
}
// 数字不进栈,数字直接进入后缀表达式中,数字可能有多位,需要特殊处理
else if (isdigit(c)) {
// 多位数字一起添加进后缀表达式中,遇到小数点也要添加
while (isdigit(expr[i]) || expr[i] == '.')
{
postExpr += expr[i];
i++;
}
// 此次循环结束后i会加一,未避免少访问一位,i需要减一
i--;
postExpr += " ";
}
// 其他字符不处理
}
// 字符串遍历完后栈中可能还存在部分操作符,需要将这些操作符全部取出来
while (!opSt.empty())
{
postExpr += opSt.top();
postExpr += " ";
opSt.pop();
}
return postExpr;
}
// 判断是否是正负号
bool isSign(string expr, int i) {
// 如果是第一个字符,那一定是正负号
if (i == 0) {
return true;
}
i--;
// 字符串中可能存在空格或者其他非法字符
while (i > 0 && !isdigit(expr[i]) && expr[i] != '/' && expr[i] != '*'
&& expr[i] != '+' && expr[i] != '-' && expr[i] != ')' && expr[i] != '(') {
i--;
}
if (isdigit(expr[i]) || expr[i] == ')'){
return false;
}
else if (!isdigit(expr[i]) && expr[i] != ')')
return true;
}上述代码为了区分各个操作数和操作符,在每次添加操作符和操作数后使用空格结尾,以空格和其他操作数和操作符间隔。
中缀表达式转换的过程比较麻烦,除了按照上面的步骤走之外还要考虑各种情况,比如加减号和正负号怎么区别,中缀表达式中的一些无用字符怎么处理,这些字符可能会影响正负号和加减号的判断结果。对应加减号和正负号的判别,我的解决方式是判断该符号前面一个字符是否是数字或者右括号,如果是则它是加减号,如果不是则它是正负号,而对应中缀表达式中的一些无用字符我直接跳过不处理,在正负号和加减号的判断中寻找该符号的前一个字符时也要跳过这些字符寻找第一个有用的字符。还有一些其他的特殊情况我没有处理,这只是一个简单的转换函数,代码的健壮性不是很强。
2. 后缀表达式求值
问题描述:
给出一个后缀表达式字符串,对其进行计算得出结果。
比如给出一个后缀表达式3 7 2 2 / * +,计算得到其结果10。
解决过程:
1. 遍历后缀表达式:
? ? ? ? 1.1. 如果当前字符是操作数,将整个操作数添加进操作数栈numSt中;
? ? ? ? 1.2. 如果当前字符是操作符:
? ? ? ? ? ? ? ? 1.2.1. 则依次从numSt中取出两个操作数num1,num2,再根据操作符计算二者进行对应计算的结果;
? ? ? ? ? ? ? ? 1.2.2. 将计算结果压入栈中;
2. 将numSt的栈顶弹出;
3. 如果numSt为空:
? ? ? ? 3.1. 返回栈顶元素结果;
4. 否则打印表达式错误;
对应流程:
?
对应代码:
// 后缀表达式计算结果
float simpleCalculator(string postExpr) {
// 存储操作数
string num = "";
MyStack<double> numSt;
double result = 0.0;
double tempResult = 0.0;
for (int i = 0; i < postExpr.length(); i++) {
char c = postExpr[i];
if (c == ' ')
continue;
// 如果是数字或者数字的正负号,可能有多位,以空格间隔
if (isdigit(c) || ((c == '-' || c == '+') && i + 1 < postExpr.length() && isdigit(postExpr[i + 1]))) {
num = "";
while (postExpr[i] != ' ' && i < postExpr.length())
{
num += postExpr[i++];
}
// 将字符串转换为double类型压入栈中
numSt.push(stod(num));
}
else if(c != ' ') {
double opNum2 = 0, opNum1 = 0;
// 从栈中取出两个数,作为操作数,注意操作顺序,最上面元素的是在双目运算符的后面
// 取栈顶元素前都需要进行非空判断
if (numSt.empty()){
cout << "表达式错误!!!请重新输入。" << endl;
//cout << result << endl;
exit(1);
}
opNum2 = numSt.top(); numSt.pop();
if (numSt.empty()){
cout << "表达式错误!!!请重新输入。" << endl;
//cout << result << endl;
exit(1);
}
opNum1 = numSt.top(); numSt.pop();
// 对应操作符对两个操作数进行相应的操作
if (c == '+') {
tempResult = opNum1 + opNum2;
}
if (c == '-') {
tempResult = opNum1 - opNum2;
}
if (c == '*') {
tempResult = opNum1 * opNum2;
}
if (c == '/') {
if (opNum2 == 0) {
cout << "出现除0错误!!!请重新输入表达式。" << endl;
exit(1);
}
tempResult = opNum1 / opNum2;
}
// 运算完后将结果压入栈中
numSt.push(tempResult);
}
}
result = numSt.top();
numSt.pop();
if (numSt.empty()) {
return result;
}
else {
cout << "表达式错误!!!请重新输入。" << endl;
exit(1);
}
}对应操作数需要一些比较复杂的判断,因为操作数可能包含符号,对于数字字符则直接将操作数整个转换为浮点数后添加进栈中直到空格为止,对应'+'、'-'号,需要判断它是否是操作数正负号,如果是则于操作数一样的操作。
测试:
string expr = "-13.21 + 1.2002 * (-21.9 + 7 * (2.2 - 8) / 2.1 - 2) - 1 + (2.0220 - 9.7 * -81.9) + -1.209";
string postExpr = cvrtExpr(expr);
cout << "后缀表达式为:" << postExpr << endl;
double calResult = simpleCalculator(postExpr);
cout << "后缀表达式计算结果:" << setprecision(10) << calResult << endl;
double s = -13.21 + 1.2002 * (-21.9 + 7 * (2.2 - 8) / 2.1 - 2) - 1 + (2.0220 - 9.7 * -81.9) + -1.209;
cout << "验证:" << setprecision(10) << s << endl;测试结果:

因为浮点数存储的方式的问题,浮点数计算会出现一些误差,所以在小数点后几位会有一些差别,但前面的结果都是一样的,再换一个位数更小的表达式测试结果。、
这次不设置保留精度,让它自己根据结果输出
string expr = "-13.2 + 1.2 * (-21.9 + 7 * (2.2 - 8) / 2.1 - 2) - 1 + (2.5 - 9.7 * -81.9) + -1.9";
string postExpr = cvrtExpr(expr);
cout << "后缀表达式为:" << postExpr << endl;
double calResult = simpleCalculator(postExpr);
cout << "后缀表达式计算结果:" << calResult << endl;
double s = -13.2 + 1.2 * (-21.9 + 7 * (2.2 - 8) / 2.1 - 2) - 1 + (2.5 - 9.7 * -81.9) + -1.9;
cout << "验证:" << s << endl;测试结果:

可以看到这次结果就一样了。?
把这两个函数结合在一起使用就相当于是一个简易的计算器了,不过对浮点数计算精度不是太高,一般小数点前三位是比较精确的。
表达式转换和后缀表达式求值原理都很简单,但是实现起来就会遇到各种问题,需要综合考虑各种问题,各种情况并一一解决,实现起来还是有点难度的。
四、总结
栈也是线性表的一种,它遵循”后进先出“的原则,即后进入栈的元素先取出。栈的操作都只能在栈顶进行,删除元素只能删除栈顶元素,插入元素只能插入在栈顶,栈的删除和插入操作对应为入栈和出栈操作,基于这个特殊的插入和删除元素的方式,栈的元素取出的原则是”后进先出“,因为后进栈的元素位于栈中更靠近栈顶的为止,先进栈的会更靠近栈底,在从栈顶元素依次出栈的过程中后进栈的因素会比先先出栈的因素先出栈。
栈的基本操作非常简单,因为只需要考虑栈顶因素的增删查,使用顺序表来存储栈实现起来也很简单,将元素依次加入数组的后面位置,以一个栈顶索引指向栈顶,使用该索引对数组中对应的元素操作就能完成对栈顶的增删查操作,不过使用数组存储需要考虑数组的大小,数组申请不了太大的空间,使用链表存储就不需要太担心这个问题。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!