【每日一题】2132. 用邮票贴满网格图-2023.12.14

题目：

2132. 用邮票贴满网格图

给你一个?m x n?的二进制矩阵?grid?，每个格子要么为?0?（空）要么为?1?（被占据）。

给你邮票的尺寸为?stampHeight x stampWidth?。我们想将邮票贴进二进制矩阵中，且满足以下?限制?和?要求?：

1. 覆盖所有?空?格子。
2. 不覆盖任何?被占据?的格子。
3. 我们可以放入任意数目的邮票。
4. 邮票可以相互有?重叠?部分。
5. 邮票不允许?旋转?。
6. 邮票必须完全在矩阵?内?。

如果在满足上述要求的前提下，可以放入邮票，请返回?true?，否则返回?false?。

示例 1：

输入：grid = [[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0]], stampHeight = 4, stampWidth = 3
输出：true
解释：我们放入两个有重叠部分的邮票（图中标号为 1 和 2），它们能覆盖所有与空格子。

示例 2：

输入：grid = [[1,0,0,0],[0,1,0,0],[0,0,1,0],[0,0,0,1]], stampHeight = 2, stampWidth = 2 
输出：false 
解释：没办法放入邮票覆盖所有的空格子，且邮票不超出网格图以外。

提示：

• m == grid.length
• n == grid[r].length
• 1 <= m, n <= 105
• 1 <= m * n <= 2 * 105
• grid[r][c]?要么是?0?，要么是?1?。
• 1 <= stampHeight, stampWidth <= 105

解答：

?

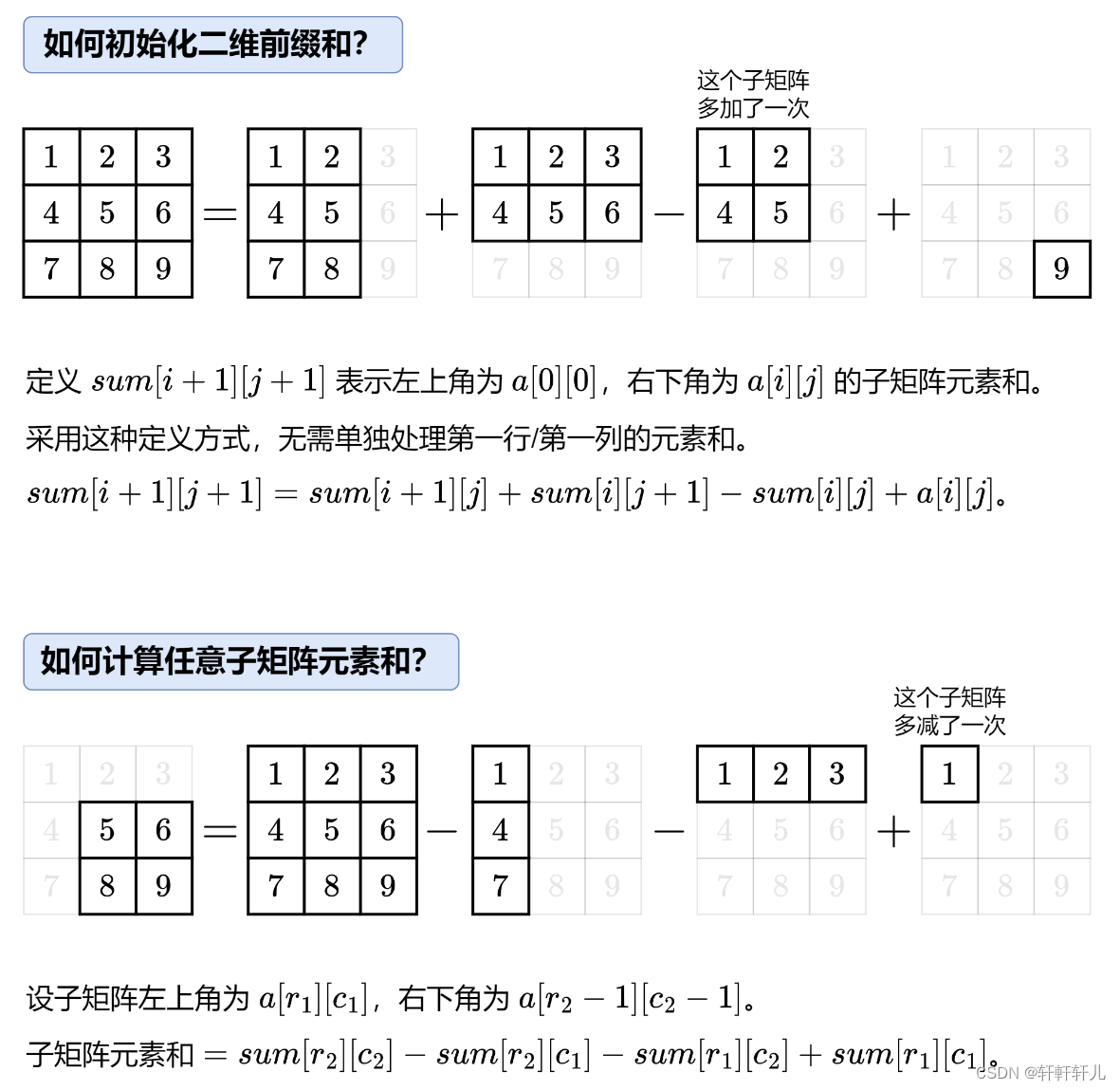代码：

class Solution {
    public boolean possibleToStamp(int[][] grid, int stampHeight, int stampWidth) {
        int m=grid.length;
        int n=grid[0].length;
        //1.计算grid的二维前缀和
        int[][] s=new int[m+1][n+1];
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                s[i+1][j+1]=s[i+1][j]+s[i][j+1]-s[i][j]+grid[i][j];
            }
        }
        //2.计算二维差分
        //为了方便第三步的计算，在d数组的最上面和最左边各加了一行(列)，所以下标要+1
        int[][] d=new int[m+2][n+2];
        for(int i2=stampHeight;i2<=m;i2++){
            for(int j2=stampWidth;j2<=n;j2++){
                int i1=i2-stampHeight+1;
                int j1=j2-stampWidth+1;
                if(s[i2][j2]-s[i2][j1-1]-s[i1-1][j2]+s[i1-1][j1-1]==0){
                    d[i1][j1]++;
                    d[i1][j2+1]--;
                    d[i2+1][j1]--;
                    d[i2+1][j2+1]++;
                }
            }
        }
        //3.还原二维差分矩阵对应的计数矩阵(原地计算)
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                d[i+1][j+1]+=d[i+1][j]+d[i][j+1]-d[i][j];
                if(grid[i][j]==0&&d[i+1][j+1]==0){
                    return false;
                }
            }
        }
        return true;
    }
}

结果：