数据结构排序——选择排序与堆排序（c语言实现）

数据结构排序——选择排序与堆排序（c语言实现）

今天继续排序的内容：

---

---

1.选择排序

1.1基本介绍

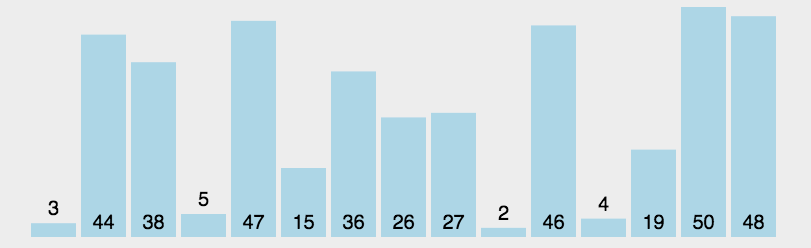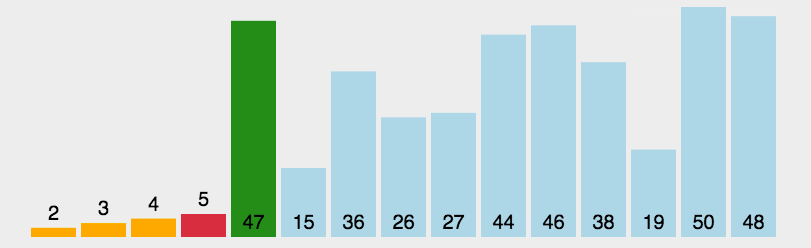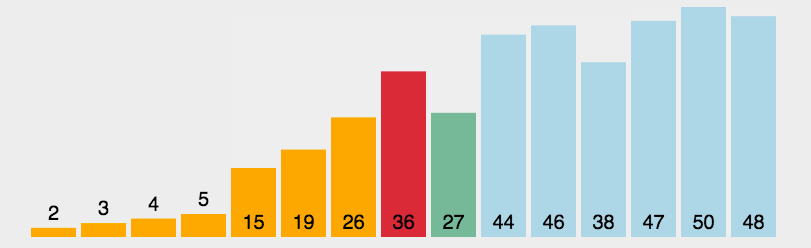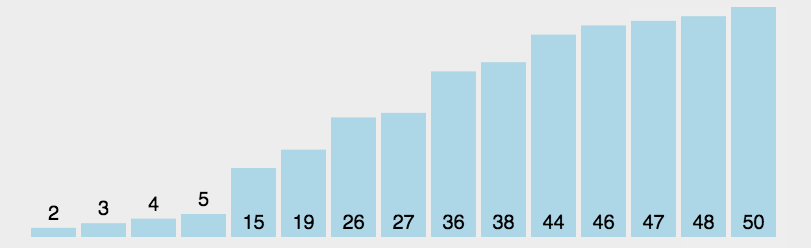
选择排序（Selection Sort）:是一种简单直观的排序算法.它的基本思想是在未排序序列中找到最小（大）的元素，放到序列的起始位置，然后再从剩余未排序元素中找到最小（大）的元素，放到已排序序列的末尾。重复这个过程，直到所有元素都排好序。

选择排序的特性：

1. 直接选择排序思考非常好理解，但是效率不是很好,所以很少使用
2. 时间复杂度：O(N^2)
3. 空间复杂度：O(1)
4. 稳定性：不稳定

1.2代码实现

1.2.1基础款

void Swap(int* x, int* y)
{
	int tmp = *x;
	*x = *y;
	*y = tmp;
}

void SelectSort(int* a, int n)//升序
{
	for (int i = 0; i < n-1; i++)//n个数据，排n-1次
	{
		int mini = i;//0到i-1都已经排好，下一个就放在i这个位置上
		for (int j = i+1; j < n; j++)//从i到n-1找最小的，因为本身是i，所以j可以中i+1开始
		{
			if (a[minf] > a[j])
			{
				minf = j;//找到小的就来替换
			}
		}
		Swap(&a[minf], &a[i]);
	}
}

int main()
{
	int a[] = { 9,1,2,5,7,4,8,6,3,5,1,2,3,5,1,8,3 };
	printf("排序前：");
	for (int i = 0; i < sizeof(a) / sizeof(int); i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
	SelectSort(a, sizeof(a) / sizeof(int));
	printf("排序后：");
	for (int i = 0; i < sizeof(a) / sizeof(int); i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
	return 0;
}

1.2.2进阶款

之前都是一次选一个最小的放在左侧。现在一次选出最大和最小，分别放在左侧和右侧

void SelectSort(int* a, int n)//升序
{
	int begin = 0, end = n - 1;
	while (begin < end)	//begin=end时就已经排好了
	{
		int mini = begin, maxi = begin;//不知道会指向哪里，所以要每次都初始化
		for (int i = begin + 1; i <= end; i++)//从begin到end找最大和最小
		{
			if (a[i] < a[mini])
			{
				mini = i;
			}
			if (a[i] > a[maxi])
			{
				maxi = i;
			}
		}
		Swap(&a[begin], &a[mini]);//最小跟begin换
		if (begin == maxi)//有可能begin位置就是此时最大的，maxi=begin，要是交换了，maxi值就不对了
		{
			maxi = mini;//让maxi仍是最大的数据的索引（此时数据被换到mini所指）
		}
		Swap(&a[end], &a[maxi]);
		begin++;
		end--;
	}

}

---

2.堆排序

2.1基本介绍

之前在堆应用这篇文章我已经讲过了堆排序和TOP-K问题，详细可见：堆的应用：堆排序和TOP-K问题

那这次就再次大致讲解一下

如果是升序，就建立大堆；是降序就建立小堆。

因为思路是（以升序为例）：大堆的堆顶一定是最大的，我们就把堆顶与堆尾交换后，除去最后一个对新堆顶进行向下调整。完成后，堆顶与倒数第二个交换…

2.2代码实现

#define _CRT_SECURE_NO_WARNINGS 1
#include"Heap.h"

void Swap(HPDataType* p1, HPDataType* p2)
{
	HPDataType tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

void AdjustUp(HPDataType* a, int child)
{
	int father = (child - 1) / 2;
	while (child > 0)
	{
		if (a[child] > a[father])
		{
			Swap(&a[child], &a[father]);
			//更新下标
			child = father;
			father = (father - 1) / 2;
		}
		else
		{
			break;//一旦符合小堆了，就直接退出
		}
	}
}

void AdjustDown(HPDataType* a, int n, int father)
{
	int child = father * 2 + 1;//假设左孩子大
	while (child < n)
	{
		if (child + 1 < n && a[child] < a[child + 1])
		{
			child++;
		}
		if (a[child] > a[father])
		{
			Swap(&a[child], &a[father]);
			father = child;
			child = father * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

void HeapSort(int* arr, int n)//升序
{
	//先建大堆
	for (int i = 0; i < n; i++)
	{
		AdjustUp(arr, i);
	}
	int a = n - 1;
	while (a > 0)
	{
		//此时最大的是堆顶，堆顶跟最后一个交换
		Swap(&arr[0], &arr[a]);
		//现在最大的已经在最后了，不考虑它，把新塔顶降下来，重新编程大堆
		AdjustDown(arr, a, 0);
		a--;
	}

}

int main()
{
	int arr[]= { 4,6,2,1,5,8,2,9 };
	for (int i = 0; i < sizeof(arr) / sizeof(int); i++)
	{
		printf("%d ", arr[i]);
	}
	printf("\n");
	HeapSort(arr, sizeof(arr) / sizeof(int));
	for (int i = 0; i < sizeof(arr) / sizeof(int); i++)
	{
		printf("%d ", arr[i]);
	}
}

---

这次就到这里啦，感谢大家支持！！！