算法设计与分析复习1

课后练习

2.1?（2）（4）（5）

2.2 ?

2.5（1）（2）

2.8 ?

实验1 复习：快速排序

• 实验任务

应用快速排序算法，对n个记录序列a1，a2，…，an-1，an进行升序排序。

• 目标

（1）编写递归函数，记录采用练习题3.4（3）。

（2）运行结果截图，分析时间复杂度，给出分析过程和分析结果。

实验1：快速排序

运行结果：

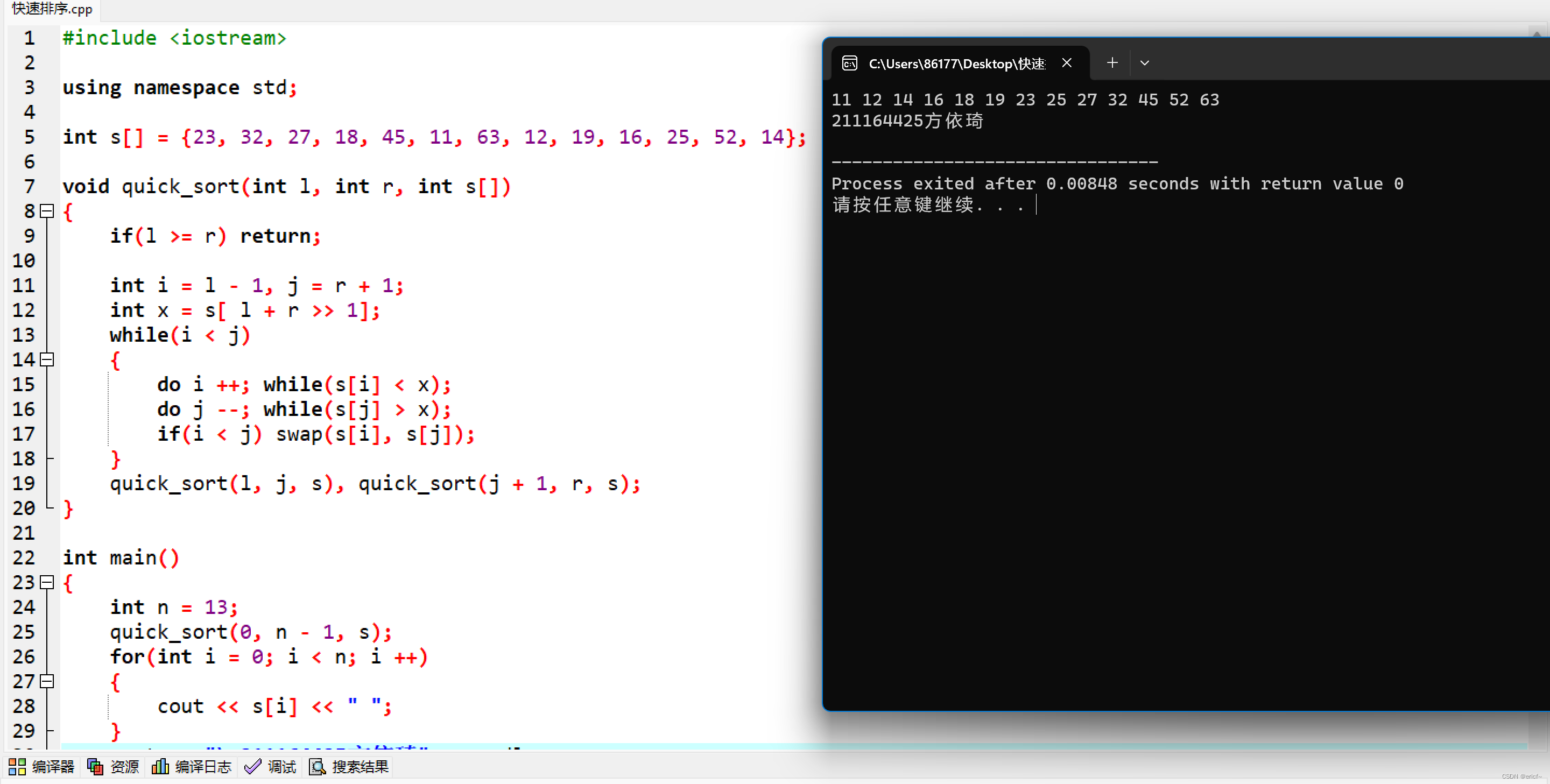
代码：

#include <iostream>



using namespace std;



int s[] = {23, 32, 27, 18, 45, 11, 63, 12, 19, 16, 25, 52, 14};



void quick_sort(int l, int r, int s[])

{

if(l >= r) return;



int i = l - 1, j = r + 1;

int x = s[ l + r >> 1];

while(i < j)

{

do i ++; while(s[i] < x);

do j --; while(s[j] > x);

if(i < j) swap(s[i], s[j]);

}

quick_sort(l, j, s), quick_sort(j + 1, r, s);

}



int main()

{

int n = 13;

quick_sort(0, n - 1, s);

for(int i = 0; i < n; i ++)

{

cout << s[i] << " ";

}

cout << "\n211164425方依琦" << endl;

return 0;

}

时间复杂度：

递归算法的时间复杂度 = 递归层数 * 每层的计算量

每层计算量O(n), 然后一共会递归logn层，时间复杂度为：O(n * logn)

由于我们每次取的都是中间元素，所以这就是快排最优的时间复杂度，这是因为平均每次分割我们都能得到较均匀的两部分。需要注意的是，在代码中使用 (l + r) >> 1 选择基准元素，在某些分布不均的数组上可能会退化到最坏情况。通常，为了提高性能并减小达到最坏情况的可能性，我们可以随机选择一个划分元素或使用"三数取中"法来选取基准元素。

分析结果:

综合最好、平均和最坏情况，可得出结论：快速排序的平均时间复杂度为 O(n * logn)

，最坏情况时间复杂度为 O(n * n)，但通常情况下可以通过随机化选择基准元素来避免最坏情况的发生，使得实际性能非常接近平均情况。

实验2 复习：最大子段和

• 实验任务

求序列(-20, 11, -4, 13, -5, -2)的最大连续子段和。

• 目标

（1）使用分治方法实现。

（2）分析时间、空间复杂度，结果截图。

实验二: 最大字段和

运行结果：

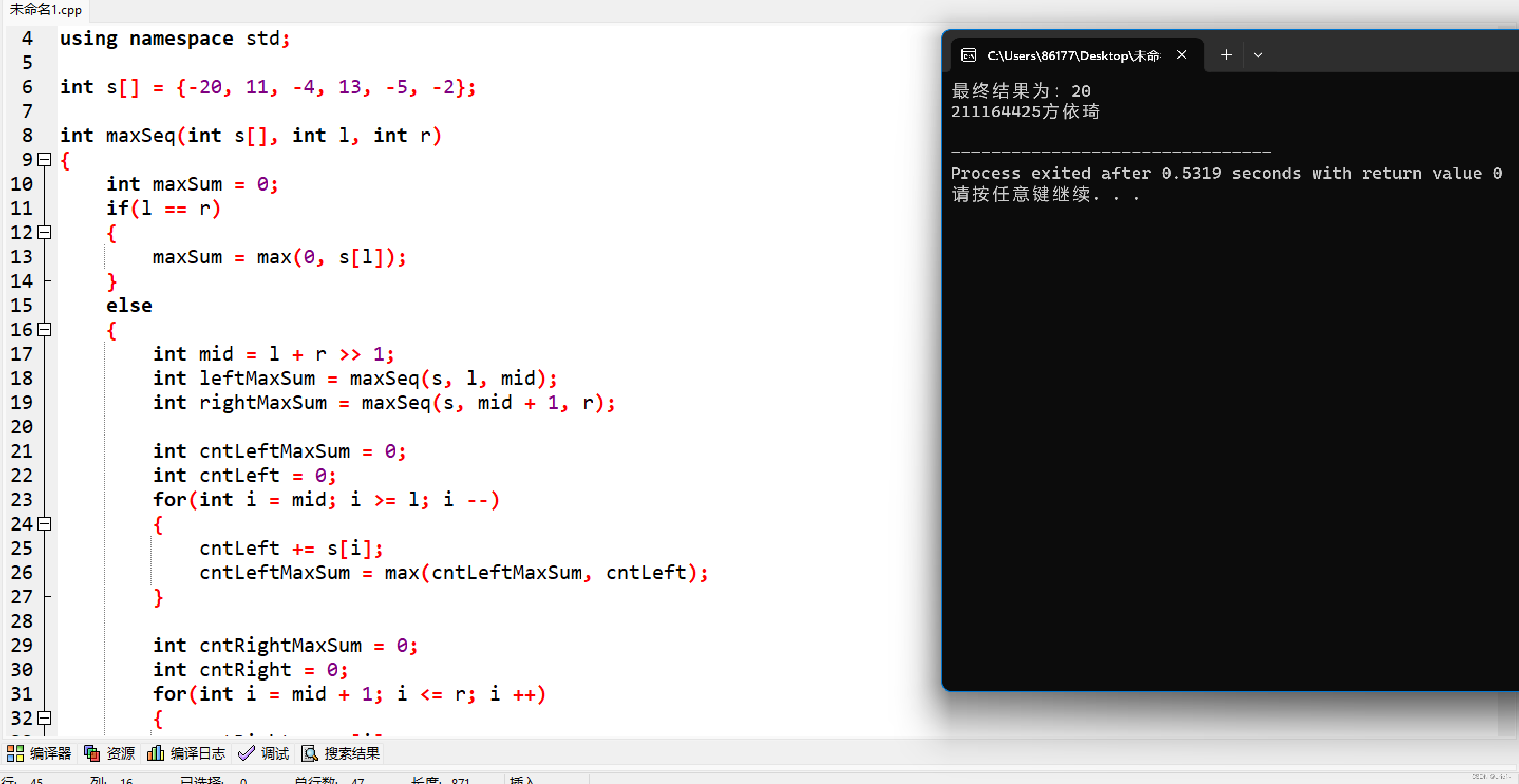
代码：

#include <iostream>



using namespace std;



int s[] = {-20, 11, -4, 13, -5, -2};



int maxSeq(int s[], int l, int r)

{

int maxSum = 0;

if(l == r)

{

maxSum = max(0, s[l]);

}

else

{

int mid = l + r >> 1;

int leftMaxSum = maxSeq(s, l, mid);

int rightMaxSum = maxSeq(s, mid + 1, r);



int cntLeftMaxSum = 0;

int cntLeft = 0;

for(int i = mid; i >= l; i --)

{

cntLeft += s[i];

cntLeftMaxSum = max(cntLeftMaxSum, cntLeft);

}



int cntRightMaxSum = 0;

int cntRight = 0;

for(int i = mid + 1; i <= r; i ++)

{

cntRight += s[i];

cntRightMaxSum = max(cntRightMaxSum, cntRight);

}

maxSum = max(leftMaxSum, max(rightMaxSum, cntLeftMaxSum + cntRightMaxSum));

}

return maxSum;

}





int main()

{

cout << "最终结果为：" << maxSeq(s, 0, 5);

cout << "\n211164425方依琦" << endl;

return 0;

}

时间复杂度：

递归算法的时间复杂度 = 递归层数 * 每层的计算量

每层计算量O(n), 然后一共会递归logn层，时间复杂度为：O(n * logn)

空间复杂度：

递归的空间复杂度=递归深度*每次递归的空间复杂度

当输入N时，由于我们每次递归都把搜索范围缩小一半，也就是N/2/2/2…直到得到1，于是有公式N/2^k=1，推出递归深度k=log_2 N每次递归的空间复杂度是个常量，为O(1)。因为递归算法那个参数，由于是数组名做参数，传递的是地址并不是把数组一个一个赋值，所以递归的空间复杂度为O(logN)。从整个算法来看，空间复杂度为O(N + logN), 所以空间复杂度为O(N);