基于C++的简单BP神经网络（C++）

需求：在某些无网络的实验机器上，由于某些任务需求，需要拟合特定的函数，因此需要部署基于C++开发的神经网络，本文在不使用外部库的情况下，编写简单的神经网络，实现简单函数的拟合。

一、简介

本文描述了一个用C++编写的反向传播（Backpropagation）神经网络，该网络采用多层感知器（MLP）结构，解决分类和预测问题，使用梯度下降算法优化权重。

二、原理

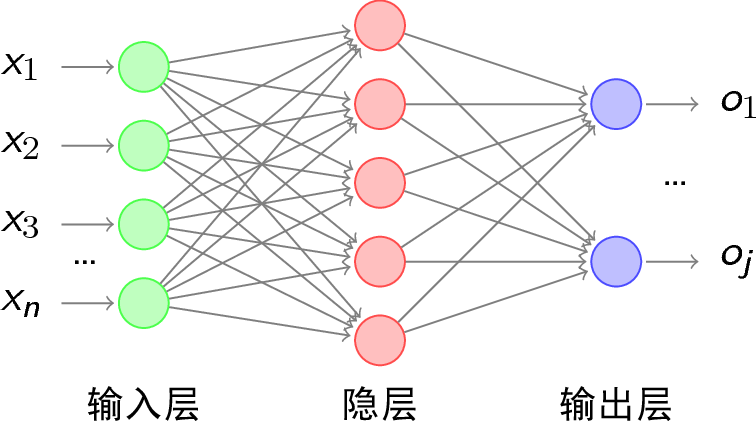
BP神经网络由输入层、隐藏层和输出层组成。每个层中的节点通过权重连接到下一层的节点。网络接收输入数据，通过激活函数（本文采用Relu）处理并传递到输出层，然后与目标输出进行比较，利用误差进行反向传播，更新权重以最小化误差。

三、代码详解

• 首先包含一些头文件，用于导入一些标准库和第三方库，例如iostream，fstream，vector，cmath和random。
  下面展示一些 内联代码片。

  #include <iostream>
  #include <fstream>
  #include <vector>
  #include <cmath>
  #include <random>
  using namespace std;
  

• 定义激活函数，用于给神经元的输出增加非线性，本文采用relu 函数，它的定义是

  relu(x)=max(0,x)
  

  double relu(double x) {
  return max(0.0, x);
  }
  

• 定义一个神经元类，用于封装一个神经元的属性和方法，它包含以下几个成员变量和成员函数：

  • 权重向量，用于存储神经元的输入权重weights。

  • 偏置值，用于增加神经元的灵活性bias。

  • 输出值，用于存储神经元的激活值output。

  • 构造函数，用于初始化权重和偏置为随机值Neuron(int input_size)。

  • 前向传播函数，用于计算神经元的输出feedforward(const vector<double>& inputs)。

  • 更新权重和偏置的函数，用于根据梯度下降法更新神经元的参数update(double delta, double learning_rate, const vector<double>& inputs)。

    / 定义一个神经元类，包含权重、偏置和输出
    class Neuron {
    public:
        // 构造函数，初始化权重和偏置为随机值
        Neuron(int input_size) {
            random_device rd;
            mt19937 gen(rd());
            normal_distribution<> dis(0.0, 0.1);
            for (int i = 0; i < input_size; i++) {
                weights.push_back(dis(gen));
            }
            bias = dis(gen);
            output = 0.0;
        }
    
        // 前向传播函数，计算输出
        void feedforward(const vector<double>& inputs) {
            double sum = 0.0;
            for (int i = 0; i < inputs.size(); i++) {
                sum += inputs[i] * weights[i];
            }
            sum += bias;
            output = relu(sum);
        }
    
        // 返回输出
        double get_output() {
            return output;
        }
    
        // 返回权重
        vector<double> get_weights() {
            return weights;
        }
    
        // 返回偏置
        double get_bias() {
            return bias;
        }
    
        // 更新权重和偏置
        void update(double delta, double learning_rate, const vector<double>& inputs) {
            for (int i = 0; i < weights.size(); i++) {
                weights[i] -= learning_rate * delta * inputs[i];
            }
            bias -= learning_rate * delta;
        }
        vector<double> weights;
        double bias;
        double output;
    };
    

• 定义一个神经网络类，用于封装一个神经网络的属性和方法，例如NeuralNetwork类，它包含以下几个成员变量和成员函数：

  • 构造函数，用于初始化神经网络的结构和参数NeuralNetwork(int input_size, int hidden_size, int output_size)。

  • 前向传播函数，用于计算神经网络的输出feedforward(const vector<double>& inputs)。

  • 反向传播函数，用于根据误差反向传播算法更新神经网络的参数backprop(const vector<double>& inputs, const vector<double>& targets, double learning_rate)。

  • 训练函数，本部分核心代码，输入参数包含三个部分（文件名，迭代次数，学习率），首先读取数据文件（本文读取“data.txt”），接着迭代更新神经网络的参数，然后将参数保存到文件中train(const string& filename, int epochs, double learning_rate)。

  • 预测函数，用于给定输入，输出神经网络的预测值predict(const vector<double>& inputs)。

  • 加载函数，有了加载函数，就不用每次都进行训练，下次使用的时候直接将保存的参数文件进行加载，提高效率load(const string& filename)。

    class NeuralNetwork {
    public:
        // 构造函数，初始化神经元
        NeuralNetwork(int input_size, int hidden_size, int output_size) {
            input_size_save = input_size;
            hidden_size_save = hidden_size;
            output_size_save = output_size;
            for (int i = 0; i < hidden_size; i++) {
                hidden_layer.push_back(Neuron(input_size));
            }
            for (int i = 0; i < output_size; i++) {
                output_layer.push_back(Neuron(hidden_size));
            }
        }
    
        // 前向传播函数，计算输出
        void feedforward(const vector<double>& inputs) {
            for (int i = 0; i < hidden_layer.size(); i++) {
                hidden_layer[i].feedforward(inputs);
            }
            vector<double> hidden_outputs;
            for (int i = 0; i < hidden_layer.size(); i++) {
                hidden_outputs.push_back(hidden_layer[i].get_output());
            }
            for (int i = 0; i < output_layer.size(); i++) {
                output_layer[i].feedforward(hidden_outputs);
            }
        }
        // 反向传播函数，更新权重和偏置
        void backprop(const vector<double>& inputs, const vector<double>& targets, double learning_rate) {
            vector<double> output_errors;
            vector<double> hidden_errors;
            for (int i = 0; i < output_layer.size(); i++) {
                double output = output_layer[i].get_output();
                double error = (output - targets[i]) * (output > 0 ? 1 : 0);
                output_errors.push_back(error);
            }
            for (int i = 0; i < hidden_layer.size(); i++) {
                double hidden_output = hidden_layer[i].get_output();
                double error = 0.0;
                for (int j = 0; j < output_layer.size(); j++) {
                    error += output_errors[j] * output_layer[j].get_weights()[i];
                }
                error *= hidden_output > 0 ? 1 : 0;
                hidden_errors.push_back(error);
            }
            for (int i = 0; i < output_layer.size(); i++) {
                vector<double> hidden_outputs;
                for (int j = 0; j < hidden_layer.size(); j++) {
                    hidden_outputs.push_back(hidden_layer[j].get_output());
                }
                output_layer[i].update(output_errors[i], learning_rate, hidden_outputs);
            }
            for (int i = 0; i < hidden_layer.size(); i++) {
                hidden_layer[i].update(hidden_errors[i], learning_rate, inputs);
            }
        }
        // 训练函数，读取数据文件，进行迭代
        void train(const string& filename, int epochs, double learning_rate) {
            ifstream fin(filename);
            if (!fin) {
                cout << "无法打开数据文件" << endl;
                return;
            }
            vector<vector<double>> data;
            while (!fin.eof()) {
                vector<double> row;
                for (int i = 0; i < input_size_save+ output_size_save; i++) {
                    double x;
                    fin >> x;
                    row.push_back(x);
                }
                data.push_back(row);
            }
            fin.close();
            for (int e = 0; e < epochs; e++) {
                double total_error = 0.0;
                for (int i = 0; i < data.size(); i++) {
                    vector<double> inputs(data[i].begin(), data[i].begin() + 2);
                    vector<double> targets(data[i].begin() + 2, data[i].end());
                    feedforward(inputs);
                    backprop(inputs, targets, learning_rate);
                    for (int j = 0; j < output_layer.size(); j++) {
                        double output = output_layer[j].get_output();
                        double error = 0.5 * pow(output - targets[j], 2);
                        total_error += error;
                    }
                }
                cout << "Epoch " << e + 1 << ": Error = " << total_error << endl;
            }
            // 保存神经网络的参数到文件
            ofstream fout("net_params.txt");
            if (!fout) {
                cout << "无法打开参数文件" << endl;
                return;
            }
            // 保存输入层、隐藏层和输出层的大小
            int input_size= input_size_save; // 输入层的神经元数量
            int hidden_size = hidden_size_save; // 隐藏层的神经元数量
            int output_size= output_size_save; // 输出层的神经元数量
            fout << input_size << " " << hidden_size << " " << output_size << endl;
            // 保存隐藏层的权重和偏置
            for (int i = 0; i < hidden_layer.size(); i++) {
                vector<double> weights = hidden_layer[i].get_weights();
                double bias = hidden_layer[i].get_bias();
                for (int j = 0; j < weights.size(); j++) {
                    fout << weights[j] << " ";
                }
                fout << bias << endl;
            }
            // 保存输出层的权重和偏置
            for (int i = 0; i < output_layer.size(); i++) {
                vector<double> weights = output_layer[i].get_weights();
                double bias = output_layer[i].get_bias();
                for (int j = 0; j < weights.size(); j++) {
                    fout << weights[j] << " ";
                }
                fout << bias << endl;
            }
            fout.close();
            cout << "神经网络的参数已保存到net_params.txt文件" << endl;
        }
    
        // 预测函数，给定输入，输出预测值
        void predict(const vector<double>& inputs) {
            feedforward(inputs);
            for (int i = 0; i < output_layer.size(); i++) {
                cout << "Output " << i + 1 << ": " << output_layer[i].get_output() << endl;
            }
        }
        // 加载函数，从文件中读取神经网络的参数
        void load(const string& filename) {
            ifstream fin(filename);
            if (!fin) {
                cout << "无法打开参数文件" << endl;
                return;
            }
            // 读取输入层、隐藏层和输出层的大小
            int input_size, hidden_size, output_size;
            fin >> input_size >> hidden_size >> output_size;
            // 重新初始化神经网络
            hidden_layer.clear();
            output_layer.clear();
            for (int i = 0; i < hidden_size; i++) {
                hidden_layer.push_back(Neuron(input_size));
            }
            for (int i = 0; i < output_size; i++) {
                output_layer.push_back(Neuron(hidden_size));
            }
            // 读取隐藏层的权重和偏置
            for (int i = 0; i < hidden_layer.size(); i++) {
                vector<double> weights(input_size);
                double bias;
                for (int j = 0; j < input_size; j++) {
                    fin >> weights[j];
                }
                fin >> bias;
                // 用读取的值覆盖原来的随机值
                hidden_layer[i].weights = weights;
                hidden_layer[i].bias = bias;
            }
            // 读取输出
            // 读取输出层的权重和偏置
            for (int i = 0; i < output_layer.size(); i++) {
                vector<double> weights(hidden_size);
                double bias;
                for (int j = 0; j < hidden_size; j++) {
                    fin >> weights[j];
                }
                fin >> bias;
                // 用读取的值覆盖原来的随机值
                output_layer[i].weights = weights;
                output_layer[i].bias = bias;
            }
            fin.close();
            cout << "神经网络的参数已从net_params.txt文件加载" << endl;
        }
    
    private:
        vector<Neuron> hidden_layer;
        vector<Neuron> output_layer;
        int input_size_save;
        int hidden_size_save;
        int output_size_save;
    };
    

四、主函数实现

最核心的部分：主函数

• 创建神经网络对象nn，输入层大小为2，隐藏层大小为8，输出层大小为1，构建一个两输入，单输出的网络
• 训练函数nn.train("data.txt", 2000, 0.001)，数据来源来自data.txt文件，本文采用的是拟合y=x1+x2，训练2000次，学习率为0.001，学习完以后将参数保存为net_params.txt文件
• 加载语句，用于调用神经网络的加载函数，例如nn.load("net_params.txt")，这里被注释掉了，表示不执行。如果之前将模型训练好了，可以将nn.train("data.txt", 2000, 0.001)进行注释，执行本语句，直接加载训练好的模型参数
• 测试输入向量，用于存储测试输入的值，例如test_input = { 4, 5 }和test_input = { 8, 8 }。
• 预测语句，用于调用神经网络的预测函数，例如nn.predict(test_input)。

int main() {
    NeuralNetwork nn(2, 8, 1); // 输入层大小为2，隐藏层大小为8，输出层大小为1
    nn.train("data.txt", 2000, 0.001); // 数据文件为data.txt，迭代次数为100，学习率为0.01
   // nn.load("net_params.txt"); // 从文件中加载神经网络的参数
    vector<double> test_input = { 4, 5 }; // 测试输入
    nn.predict(test_input); // 输出预测值
    test_input = { 8, 8 }; // 测试输入
    nn.predict(test_input); // 输出预测值
    return 0;
}

可以检测输出结果为：

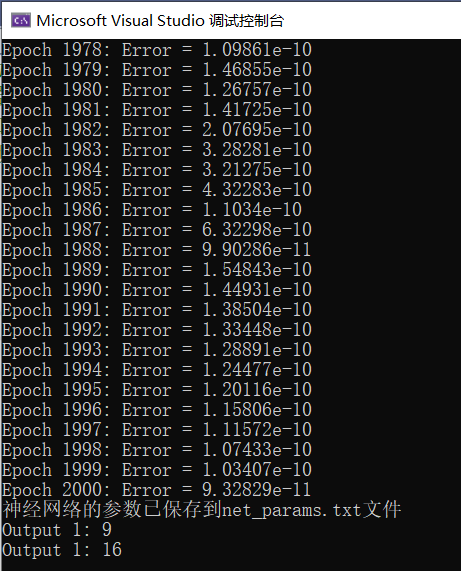
可以看到，输出误差基本为0，神经网络的参数被保存，测试输出为9和16，完美预测！

附上完整代码（包含代码，训练数据，模型参数数据）：
https://download.csdn.net/download/weixin_44346182/88628514