区间预测 | Matlab实现CNN-LSTM-KDE的卷积长短期神经网络结合核密度估计多变量时序区间预测

区间预测 | Matlab实现CNN-LSTM-KDE的卷积长短期神经网络结合核密度估计多变量时序区间预测

效果一览

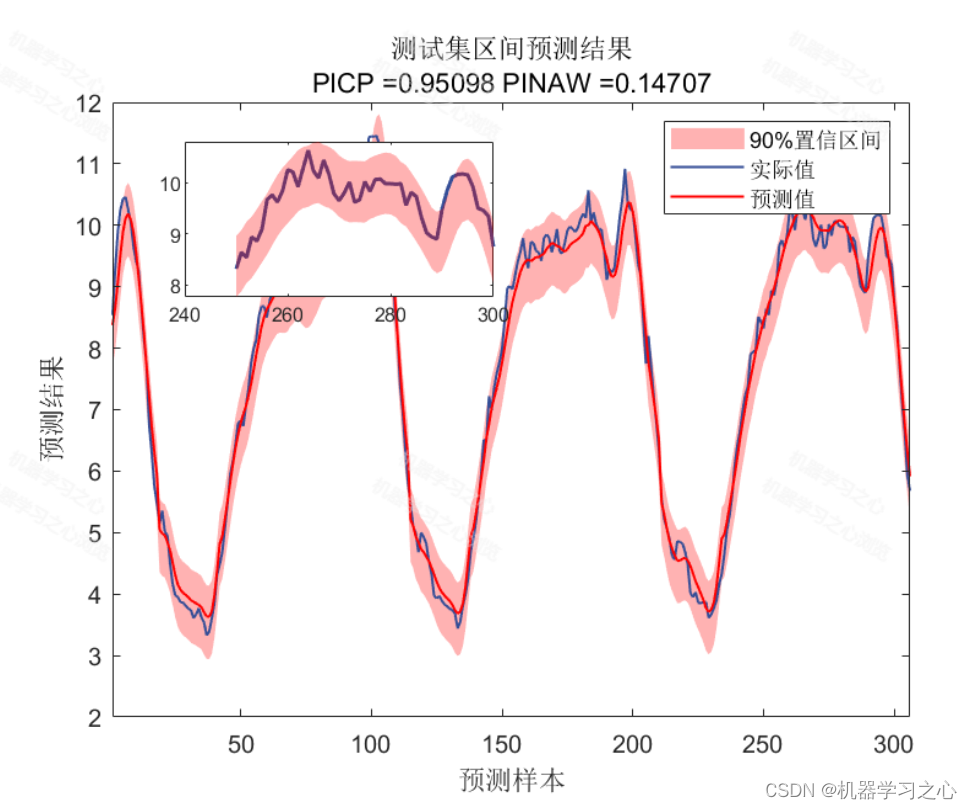
基本介绍

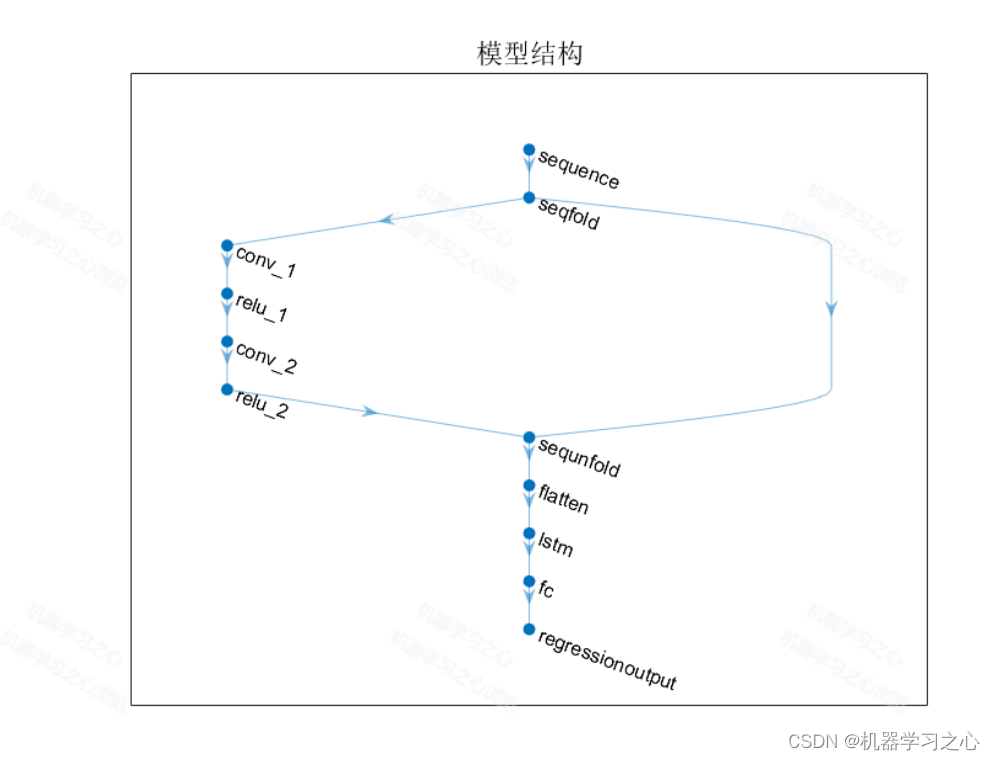
1.CNN-LSTM-KDE多变量时间序列区间预测，基于卷积长短期记忆神经网络多变量时序区间预测，卷积长短期记忆神经网络的核密度估计下置信区间预测。
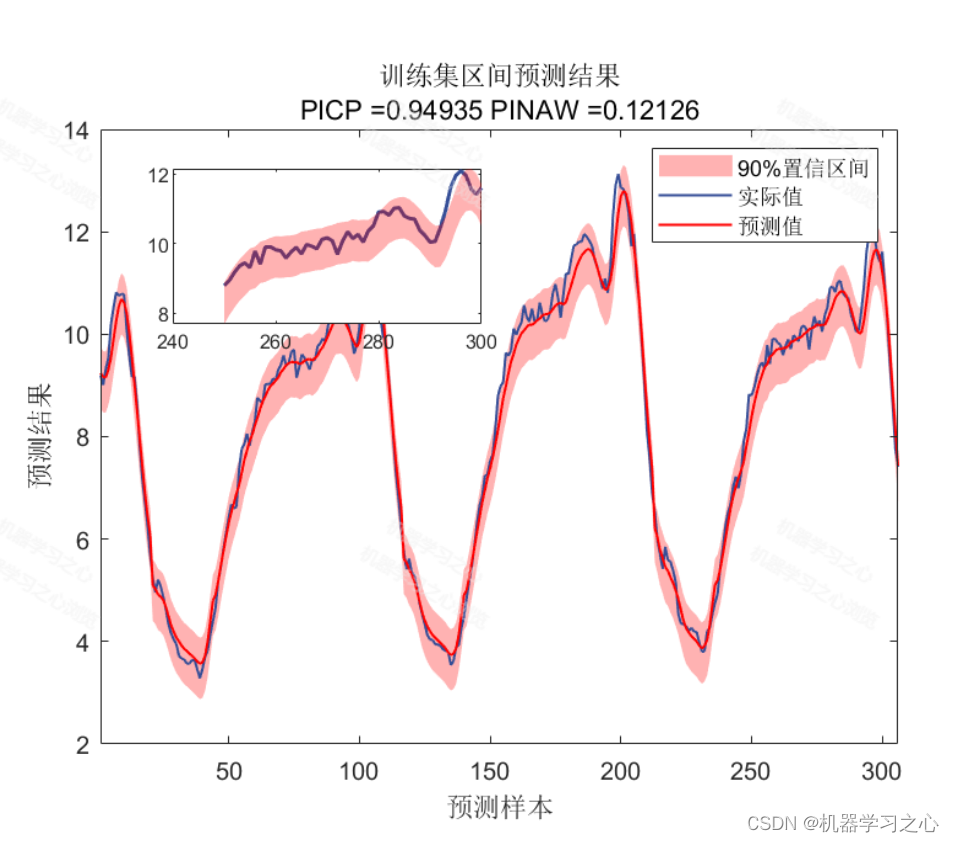
2.含点预测图、置信区间预测图、核密度估计图，区间预测(区间覆盖率PICP、区间平均宽度百分比PINAW),点预测多指标输出(R2、MAE、MAPE、MBE、 MSE),多输入单输出。
3.运行环境为Matlab2021b及以上；
4.输入多个特征，输出单个变量，考虑历史特征的影响，多变量时间序列区间预测；
5.data为数据集，main.m为主程序，运行即可,所有文件放在一个文件夹。

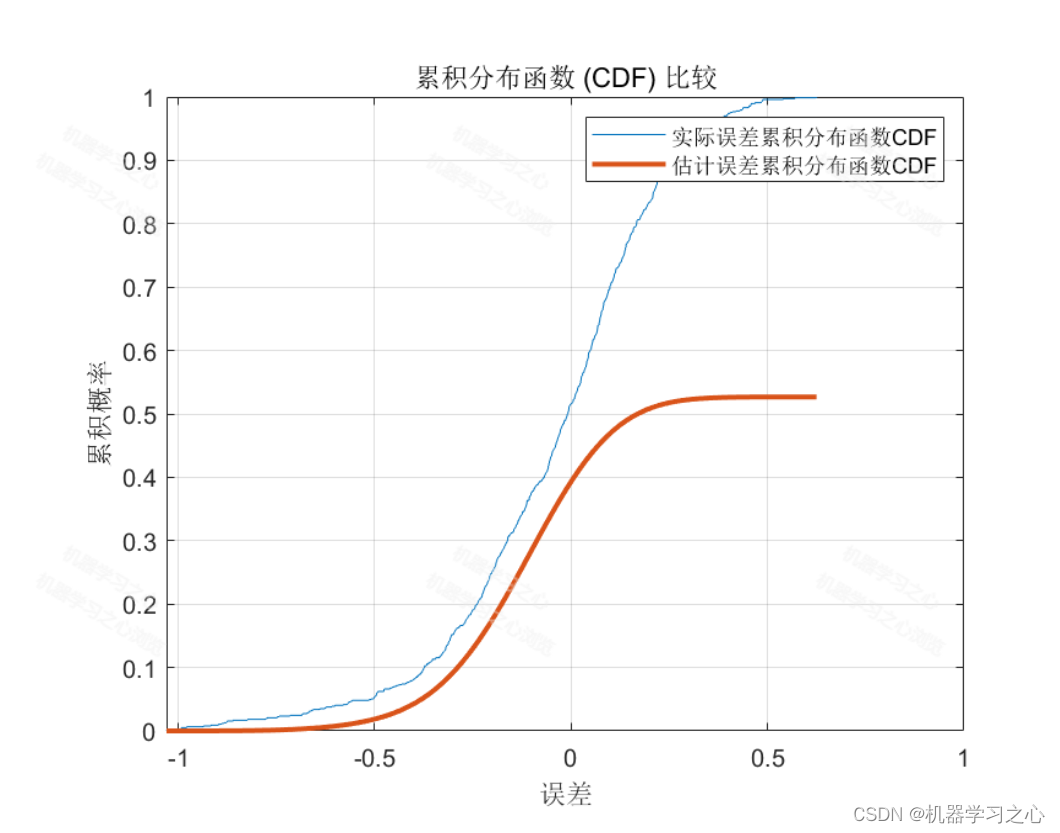
累积分布函数（CDF）
估计误差小于实际误差：估计累计误差分布的大小小于实际累计误差分布的大小。说明在误差估计方法对系统的噪声或者不确定性进行了较好的建模，并且能够对误差进行较为准确的预测。

程序设计

• 完整程序和数据获取方式：私信博主回复Matlab实现CNN-LSTM-KDE的卷积长短期神经网络结合核密度估计多变量时序区间预测。

%% 参数设置
options = trainingOptions('adam', ...     % Adam 梯度下降算法
    'MaxEpochs', 100,...                  % 最大训练次数
    'MiniBatchSize',64,...                % 批处理
    'InitialLearnRate', 0.001,...         % 初始学习率为0.001
    'L2Regularization', 0.001,...         % L2正则化参数
    'LearnRateSchedule', 'piecewise',...  % 学习率下降
    'LearnRateDropFactor', 0.1,...        % 学习率下降因子 0.1
    'LearnRateDropPeriod', 400,...        % 经过800次训练后 学习率为 0.001*0.1
    'Shuffle', 'every-epoch',...          % 每次训练打乱数据集
    'ValidationPatience', Inf,...         % 关闭验证
    'Plots', 'training-progress',...      % 画出曲线
    'Verbose', false);

%% 训练
net = trainNetwork(p_train, t_train, lgraph, options);

%% 预测
t_sim1 = predict(net, p_train); 
t_sim2 = predict(net, p_test ); 

%%  数据反归一化
T_sim1 = mapminmax('reverse', t_sim1, ps_output);
T_sim2 = mapminmax('reverse', t_sim2, ps_output);
T_sim1 =T_sim1';
T_sim2 =T_sim2';
%%  均方根误差
error1 = sqrt(sum((T_sim1 - T_train).^2) ./ M);
error2 = sqrt(sum((T_sim2 - T_test ).^2) ./ N);
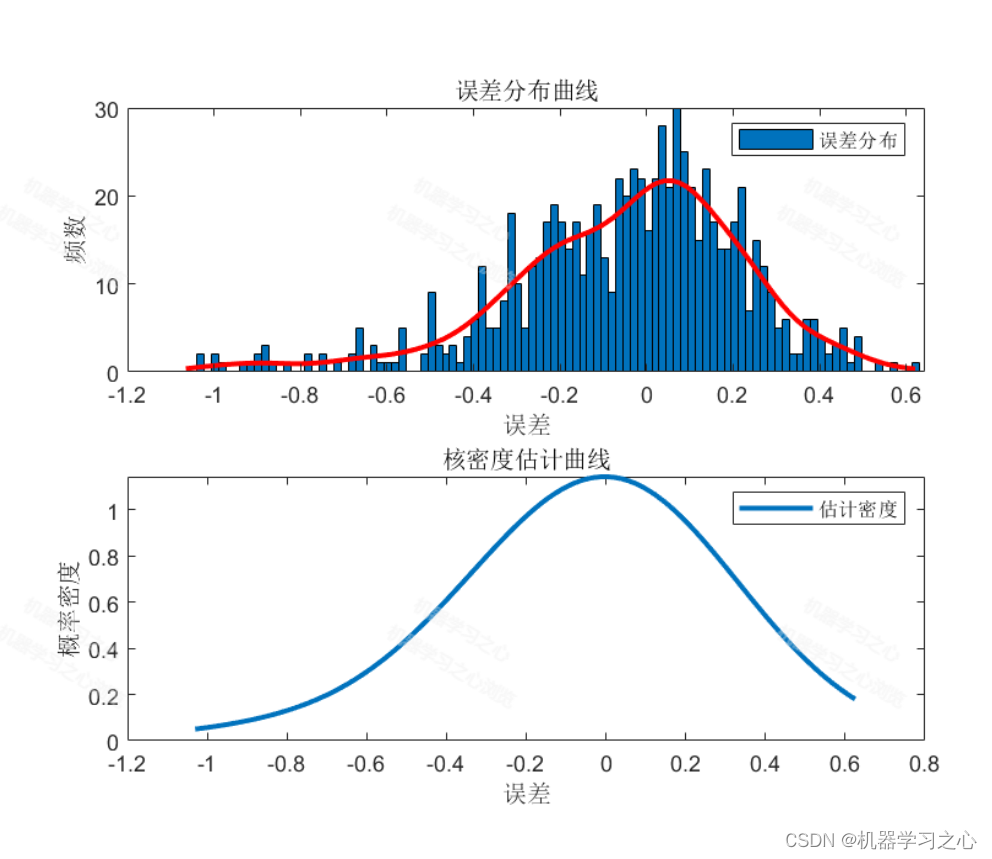
% 可视化估计的密度函数
figure;
subplot(2,1,1); 
histfit(train_errors,100,'kernel', 'Normalization', 'probability')
legend('误差分布');
xlabel('误差');
ylabel('频数');
title('误差分布曲线');
subplot(2,1,2); 

xlabel('误差');
ylabel('概率密度');
legend('估计密度');
title('核密度估计曲线');

% 累积分布函数（CDF）
% 估计误差小于实际误差：估计累计误差分布的大小小于实际累计误差分布的大小。
% 这种情况可能出现在误差估计方法对系统的噪声或者不确定性进行了较好的建模，并且能够对误差进行较为准确的预测。
figure;
cdfplot(train_errors);
hold on;
title('累积分布函数 (CDF) 比较');
xlabel('误差');
ylabel('累积概率');
legend('实际误差累积分布函数CDF', '估计误差累积分布函数CDF');
% 计算累积分布函数（CDF）
cdf_train = cumsum(f_train) * (x_train(2) - x_train(1));

参考资料

[1] https://blog.csdn.net/kjm13182345320/article/details/127931217
[2] https://blog.csdn.net/kjm13182345320/article/details/127418340