PointNet:用于3D分类和分割的点集深度学习
PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation
翻译点云论文的开山之作《 PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation》
摘要
点云是一种重要的几何数据结构。由于其格式不规则,大多数研究人员将这些数据转换为规则的3D体素网格或图像集合。然而,这使得数据不必要地庞大,并引起问题。在本文中,我们设计了一种新型的直接消耗点云的神经网络,它很好地尊重了输入点的排列不变性。我们的网络叫做PointNet,为从对象分类、部件分割到场景语义解析等应用提供了统一的体系结构。虽然简单,但PointNet非常高效的。从经验上看,它显示出与最先进的技术相当甚至更好的强大性能。从理论上讲,我们提供了分析,以理解网络已经学习了什么,以及为什么网络在输入扰动和损坏方面是鲁棒的。
1.介绍
在本文中,我们探索了能够对3D几何数据进行推理的深度学习架构,例如点云或网格。典型的卷积架构需要高度规则的输入数据格式,如图像网格或3D体素,以便执行权重共享和其他内核优化。由于点云或网格不是规则格式,大多数研究人员通常在将这些数据输入深度网络架构之前将其转换为规则的3D体素网格或图像集合(例如视图)。然而,这种数据表示转换使生成的数据变得不必要的庞大,同时还引入了量化工件,可能会模糊数据的自然不变性。
出于这个原因,我们专注于使用简单的点云对3D几何图形进行不同的输入表示,并将我们得到的深度网络命名为PointNets。点云是简单统一的结构,避免了网格的组合不规则性和复杂性,因此更容易学习。然而PointNet仍然需要考虑这样一个事实,即点云只是点的集合,因此对其成员的排列是不变的,在网络计算中需要一定的对称性。还需要考虑刚性运动的其他不变性。
我们的PointNet是一个统一的体系结构,它直接将点云作为输入和输出,要么是整个输入的类标签,要么是每个输入点的每个点段/部分标签。我们的网络的基本架构非常简单,因为在初始阶段,每个点都被相同且独立地处理。在基本设置中,每个点仅由三个坐标(x;y;z)表示。可以通过计算法线和其他局部或全局特征来添加额外的维度。
我们的方法的关键是使用一个单一的对称函数,最大池。网络有效的学习了一组优化函数/标准,这些函数/标准选择点云中感兴趣的或者信息丰富的点,并编码选择他们的原因。网络的最终全连接层将这些学习到的最优值聚合到前面提到的整个形状的全局描述符中(形状分类),或者用于预测每个点的标签(形状分割)。
我们的输入格式很容易应用刚性或仿射变换,因为每个点都独立变换。因此,我们可以添加一个与数据相关的空间转换网络,该网络试图在PointNet处理数据之前对数据进行规范化,从而进一步改进结果。
注:三维空间的变换:
刚体变换是指在三维空间中,把一个物体做旋转、平移,是一种保持物体大小和形状不变的仿射变换,刚体变换又称为欧式变换、齐次变换。
仿射变换是指物体从一个向量空间进行一次线性变换并接上一个平移,变换到另一个向量空间。平移、旋转、缩放、剪切、反射以及它们任意次序的组合都是仿射变换。

图1 pointNet应用.我们提出了一种新的网络架构,它使用原始点云(点集),而无需体素化或渲染。它是一个学习全局和局部点特征的统一体系结构,为许多3D识别任务提供了一种简单、高效和有效的方法。
我们对我们的方法进行了理论分析和实验评估。我们证明了我们的网络可以近似任何连续的集合函数。更有趣的是,我们的网络通过一个关键点的稀疏集合来学习总结一个输入点云,根据可视化大致对应对象的骨架。理论分析提供了为什么我们的PointNet对输入点的小扰动以及通过点插入(异常值)或删除(缺失数据)造成的损坏具有高度鲁棒性的理解。
在许多基准数据集上,从形状分类、部分分割到场景分割,我们通过实验将PointNet与基于多视图和体积表示的最先进方法进行了比较。在统一的体系结构下,我们的PointNet不仅在速度上快得多,而且还显示出与现有技术相当甚至更好的强大性能。
我们工作的主要贡献如下:
- 我们设计了一种新的深度网络架构,适合于在三维中使用无序点集;
- 我们展示了如何训练这样的网络来执行3D形状分类,形状部分分割和场景语义解析任务;
- 我们对该方法的稳定性和效率进行了全面的实证和理论分析
- 我们展示了由网络中选定的神经元计算的3D特征,并对其性能进行了直观的解释。
用神经网络处理无序集的问题是一个非常普遍和基本的问题——我们期望我们的想法也可以转移到其他领域。
2.相关工作
点云特征 点云的大多数现有功能都是针对特定任务手工制作的。点特征通常对点的某些统计属性进行编码,并被设计成对某些变换不变性,这些变换通常分为内在的和外在的。它们也可以分为局部特征和全局特征。对于特定的任务,找到最优的特征组合并不是一件容易的事情。
3D数据的深度学习 3D数据有多种流行的表示形式,导致学习的方法多种多样。Volumetric CNNs是将3D卷积神经网络应用于体素化形状的先驱。然而,由于数据稀疏性和三维卷积的计算成本,体积表示受到分辨率的限制。FPNN和Vote3D提出了特殊的方法来处理稀疏性问题;然而,他们的操作仍然在稀疏的体积上,处理非常大的点云对他们来说是一个挑战。**Multiview CNNs:**已经尝试将3D点云或形状 渲染成2D图像,然后应用2D转换网络对它们进行分类。通过精心设计的图像CNN,这一系列方法已经在形状分类和检索任务上取得了主导性能。然而,将它们扩展到场景理解或其他3D任务(如点分类和形状补全)是很重要的。**Spectral CNNs:**一些最新的工作在网格上使用了光谱cnn。然而,这些方法目前仅限于有机物体等流形网格,如何将其扩展到家具等非等距形状还不明显。**Feature-based DNNs:**首先将3D数据转换为向量,通过提取传统的形状特征,然后使用全连接网络对形状进行分类。我们认为它们受到所提取特征的表示能力的限制。
无序集上的深度学习 从数据结构的角度来看,点云是一组无序的向量。虽然深度学习的大多数工作都集中在常规的输入表示上,比如序列(在语音和语言处理中)、图像和体积(视频或3D数据),但在点集的深度学习方面做的工作并不多。
Oriol Vinyals等人最近的一项研究探讨了这个问题。他们使用一个具有注意力机制的read-process-write网络来处理无序的输入集,并表明他们的网络有能力对数字进行排序。然而,由于他们的工作集中在通用集合和NLP(自然语言处理)应用程序上,因此集合中缺乏几何体的作用。
3.问题陈述
我们设计了一个深度学习框架,直接使用无序点集作为输入。点云被表示为一组3D点{ P i ∣ i = 1 , … , n } 其中每个点P i是其( x , y , z ) 坐标加上额外的特征通道(例如颜色、法线等)的向量。为了简单明了,除非另有说明,我们只使用( x , y , z ) 坐标作为点的通道。
对于目标分类任务,输入点云要么直接从形状中采样,要么从场景点云中预分割。我们提出的深度网络为所有k个候选类输出k个分数。对于语义分割,输入可以是单个对象用于部分区域分割,也可以是3D场景中的子体用于对象区域分割。我们的模型将为每n点和每m语义子类别输出n × m分数。
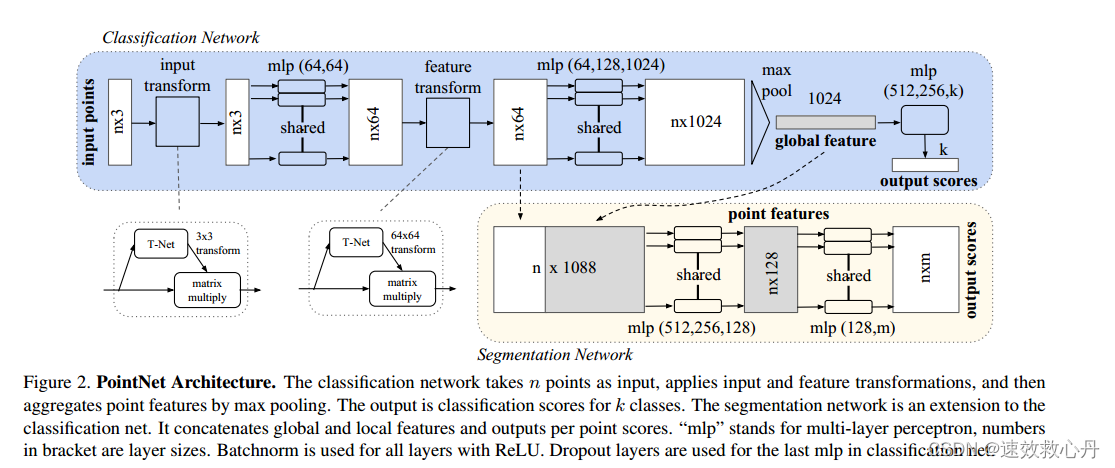
图2.PointNet架构。分类网络将n个点作为输入,应用输入和特征变换,然后通过最大池化聚合点特征。输出是k个类别的分类分数。分割网络是分类网络的扩展。它连接全局和局部特征并输出每点分数。 “mlp”代表多层感知器,括号中的数字是层大小。 [Batchnorm]学习链接(https://zhuanlan.zhihu.com/p/441573901)用于所有带有ReLU的层。Dropout层用于分类网络中的最后一个mlp。(注:Dropout可以比较有效的缓解过拟合的发生,在一定程度上达到正则化的效果)
4.点集上的深度学习
我们的网络架构(第4.2节)的灵感来自于rn中的点集(第4.1节)的属性。
4.1Rn 中点集的性质
-
无序。 与图像中的像素阵列或体积网格中的体素阵列不同,点云是一组没有特定顺序的点。换句话说,一个处理N个3D点集的网络需要在数据输入顺序上对输入集的N !排列保持不变。
-
点之间的相互作用。 这些点来自具有距离度量的空间。这意味着点不是孤立的,相邻点形成一个有意义的子集。因此,模型需要能够从附近的点捕捉局部结构,以及局部结构之间的组合相互作用。
-
变换下的不变性。 作为一个几何目标,点集的学习表示对于某些变换应该是不变的。例如,所有的点旋转和平移不应修改全局点云类别,也不应修改点的分段。
4.2 PointNet架构
我们的完整网络架构如图2所示,其中,分类网络和分割网络共享很大一部分结构。请阅读图2中传递途径的说明。
我们的网络有三个关键模块:作为对称函数聚合所有点信息的max pooling层、局部和全局信息组合结构,以及用于对齐输入点和点要素的两个联合对齐网络。
我们将在下面单独的段落中讨论这些设计选择背后的原因。
无序输入的对称函数 为了使模型对输入排列不变,存在三种策略:1)将输入按规范顺序排序;2)将输入作为一个序列来训练RNN,但通过各种排列来增加训练数据;3)使用一个简单的对称函数对每个点的信息进行聚合。这里,对称函数以n个向量作为输入,并输出一个与输入顺序不变的新向量。r.例如,+和*运算符是对称的二元函数。
虽然排序听起来像一个简单的解决方案,但在高维空间中,实际上不存在一般意义上的稳定的w.r.t.点扰动排序。这一点很容易用矛盾来说明。如果存在这样的排序策略,则定义了高维空间与一维实线之间的双射映射。不难看出,要求排序对于点扰动是稳定的,相当于要求该地图在维度减小时保持空间接近度,这是一般情况下无法完成的任务。因此,排序并不能完全解决排序问题,而且随着排序问题的持续,网络很难从输入到输出获得一致的映射。如实验所示(图5),我们发现将MLP直接应用于分类后的点集表现不佳,尽管比直接处理未分类的输入稍好。
使用RNN的想法将点集视为一个序列信号,并希望通过用随机排列的序列训练RNN,RNN将变得对输入顺序不变。然而,在“OrderMatters” 中,作者已经表明顺序确实很重要,不能完全忽视。虽然RNN对于小长度序列(几十个)的输入排序具有相对较好的鲁棒性,但很难扩展到数千个输入元素,这是点集的常见大小。经验上,我们也表明基于RNN的模型表现不如我们提出的方法(图5)。
我们的想法是通过对点集中的变换元素应用对称函数来近似定义在点集中的一般函数:
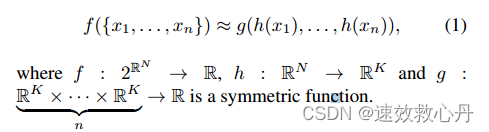
根据经验,我们的基本模块非常简单:我们通过多层感知器网络近似h,通过单变量函数和最大池化函数的组合近似g。实验证明这是有效的。通过h的集合,我们可以学习一些f来获取集合的不同性质。虽然我们的关键模块看起来很简单,但它具有有趣的属性(参见5.3节),并且可以在一些不同的应用程序中实现强大的性能(参见5.1节)。由于我们模块的简单性,我们也能够像第4.3节那样提供理论分析。
局部和全局信息聚合 上述部分的输出形成一个向量[f1; : : : ; fK],它是输入集的全局签名。我们可以很容易地在形状全局特征上训练SVM或多层感知器分类器进行分类。然而,点分割需要局部知识和全局知识的结合。我们可以通过一种简单而高效的方式来实现这一点。
我们的解决方案如图2 (Segmentation Network)所示。在计算出全局点云特征向量后,通过将全局特征与每个点特征连接起来,将其反馈给每个点特征。然后,我们在组合点特征的基础上提取新的每点特征——这一次,每点特征既知道局部信息,也知道全局信息。
通过这种修改,我们的网络能够预测依赖于局部几何和全局语义的每个点的数量。例如,我们可以准确地预测每个点的法线(图中补充),验证网络能够从点的局部邻域总结信息。在实验中,我们也证明了我们的模型在形状部分分割和场景分割方面可以达到最先进的性能。
联合校准网络 当点云经过一定的几何变换(如刚性变换)时,点云的语义标记必须是不变的。因此,我们期望通过我们的点集学习的表示对这些变换是不变的。
一个自然的解决方案是在特征提取之前将所有输入集对齐到一个规范空间。Jaderberg等人引入了空间转换器的思想,通过采样和插值来对齐2D图像,这是通过在GPU上实现的专门定制的层来实现的。
我们的点云输入形式使我们能够以一种更简单的方式实现这一目标。我们不需要创建任何新的图层,也不需要像在图片的例子中那样引入别名。我们通过一个小型网络(图2中的T-net)预测一个仿射变换矩阵,并直接将这个变换应用到输入点的坐标上。该网络本身类似于大网络,由点无关特征提取、最大池化和全连通层等基本模块组成。关于T-net的更多细节见附录。
这个想法也可以进一步扩展到特征空间的对齐。我们可以在点特征上插入另一个对齐网络,并预测一个特征变换矩阵来对齐来自不同输入点云的特征。然而,特征空间中的变换矩阵比空间变换矩阵的维数要高得多,这大大增加了优化的难度。因此,我们在softmax的训练损失中增加了一个正则化项。我们将特征变换矩阵约束为接近正交矩阵: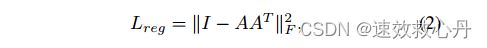
其中A为小型网络预测的特征对齐矩阵。因此,我们希望正交变换不会丢失输入中的信息。我们发现,通过加入正则化项,优化变得更加稳定,我们的模型获得了更好的性能。
4.3理论分析
通用近似 我们首先展示了我们的神经网络对连续集函数的通用近似能力。通过集合函数的连续性,直观地,对输入点集的小扰动应该不会极大地改变函数值,例如分类或分割分数。


参考来自:
https://blog.csdn.net/qq_25763027/article/details/123312646
Hausdorff距离可以理解成一个点集中的点到另一个点集的最短距离的最大值

图 3. 部分分割的定性结果。我们可视化所有16个目标类别的CAD部分分割结果。我们展示了部分模拟Kinect扫描(左块)和完整ShapeNet CAD 模型(右块)的结果。
定理1

这个定理的证明可以在我们的补充材料中找到。关键思想是,在最坏的情况下,网络可以通过将空间划分为大小相等的体素来学习将点云转换为体积表示。然而在实践中,网络学习了一种更智能的策略来探测空间,正如我们将在点函数可视化中看到的那样。
Bottleneck dimension and stability 维数障碍和稳定性从理论上和实验上我们发现,我们的网络的表达性受到最大池化层的维度,即K 在(1)中的强烈影响。这里我们提供了一个分析,它也揭示了与我们的模型稳定性相关的属性。
sub-network:子网络
map:映射
dimensional:维度
vector:矢量
symmetric:对称的;匀称的
下面的定理告诉我们,输入集中的小损坏或额外的噪声点不太可能改变我们网络的输出:
定理2我们解释这个定理的含义。
(a)如果CS中的所有点都被保留,f(S)在输入损坏之前是不变的;它也没有改变额外的噪声点高达NS。
(b)表示CS只包含有限数量的点,由(1)中的K决定。换句话说, f(S)实际上完全由小于或等于K个元素的有限子集CS? S决定 。因此,我们也称CS为S的临界点集,称K为f的瓶颈维数。
结合h的连续性,这解释了我们的模型w.r.t点扰动、损坏和额外噪声点的鲁棒性。鲁棒性的获得与机器学习模型中的稀疏性原理类似。直观地说,我们的网络学习通过一组稀疏的关键点来总结形状。在实验部分,我们看到关键点构成了一个物体的架构。
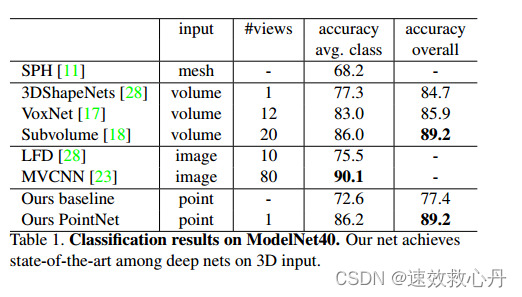
表1 ModelNet40上的分类结果。我们的网络在3D输入的深度网络中达到了最先进的水平。
5.实验
实验分为四个部分。首先,我们展示了PointNet可以应用于多个3D识别任务(第5.1节)。 其次,我们提供详细的实验来验证我们的网络设计(第5.2节)。 最后,我们将网络学习的内容可视化(第5.3节),并分析时间和空间复杂性(第5.4节)。
5.1 应用
在本节中,我们将展示如何训练我们的网络来执行3D对象分类、对象部分分割和语义场景分割。尽管我们正在研究一种全新的数据表示(点集),我们能够在几个任务的基准测试中获得相当甚至更好的性能。
3D目标分类 我们的网络学习可用于目标分类的全局点云特征。我们在ModelNet40形状分类基准上评估我们的模型。有来自40个人造物体类别的12,311个CAD模型,分为9843个用于训练,2468个用于测试。虽然以前的方法侧重于体积和多视图图像表示,但我们是第一个直接处理原始点云的方法。
我们按照面面积对网格面上的1024个点进行均匀采样,并将其归一化为单位范围。在训练过程中,我们通过沿上轴随机旋转物体来增加点云,并通过均值为零、标准差为0.02的高斯噪声来抖动每个点的位置。
在表1中,我们将我们的模型与之前的作品以及我们使用MLP对从点云提取的传统特征(点密度、D2、形状轮廓等)进行的基线进行了比较。我们的模型在基于3D输入(体积和点云)的方法中实现了最先进的性能。只有完全连接的层和最大池化,我们的网络在推理速度上获得了强大的领先优势,并且可以很容易地在CPU上并行化。我们的方法与基于多视图的方法(MVCNN[23])之间仍有很小的差距,我们认为这是由于渲染图像可以捕获的精细几何细节的损失。
3D目标部分分割部分分割是一项具有挑战性的细粒度3D识别任务。给定3D扫描或网格模型,任务是为每个点或面分配部分类别标签(例如椅子腿、杯柄)。
我们对来自[29]的ShapeNet部分数据集进行评估,它包含16个类别的16,881个形状,总共注释了50个部分。大多数对象类别被标记为两到五个部分。在形状上的采样点上标记基础真值注释。
我们将部分分割描述为逐点分类问题。在点上的评估指标为mIoU。(注:平均交并比(Mean Intersection over Union),也称为平均IoU(Intersection over Union))对于C类的每个形状S,计算形状的mIoU:对于C类中的每种部分类型,计算出基本事实和预测之间的IoU。 如果根据真值和预测点的并集为空,则将部分IoU计为1。然后我们对C类中所有部分类型的mIOU进行平均,得到该形状的mIoU。为了计算类别的mIoU,我们取该类别中所有形状的mIoU的平均值。
在本节中,我们将我们的分割版本PointNet(图2的修改版本,分割网络)与两种传统方法 [27] 和 [29] 进行比较,这两种方法都利用了逐点几何特征和形状之间的对应关系,以及我们自己的3D CNN基线。有关3D CNN的详细修改和网络架构,请参阅补充。
在表2中,我们报告了每个类别和平均IoU(%)分数。 我们观察到平均IoU改善了2.3%,我们的净改善率超过了大多数类别的基线方法。

表2. ShapeNet部分数据集的分割结果。度量标准是点上的mIoU(%)。我们与两种传统方法 [27] 和 [29] 以及我们提出的 3D 全卷积网络基线进行比较。我们的PointNet方法在 mIoU 中达到了最先进的水平。
我们还对模拟Kinect扫描进行了实验,以测试这些方法的鲁棒性。对于ShapeNet部分数据集中的每个CAD模型,我们使用Blensor Kinect 模拟器[7]从六个随机视点生成不完整的点云。 我们使用相同的网络架构和训练设置在完整的形状和部分扫描上训练我们的PointNet。结果表明,我们只损失了5.3%的平均IoU。在图3中,我们给出了完整数据和部分数据的定性结果。可以看出,虽然部分数据相当具有挑战性,但我们的预测是合理的。
场景中的语义分割 我们的部分分割网络可以很容易地扩展到语义场景分割,其中点标签成为语义对象类而不是对象部分标签。我们在 Stanford 3D语义解析数据集[1]上进行实验。该数据集包含来自6个区域(包括271个房间)的Matterport扫描仪的3D扫描。扫描中的每个点都用来自13个类别(椅子、桌子、地板、墙壁等加上杂乱)的语义标签之一进行注释。
为了准备训练数据,我们首先按房间分割点,然后将房间采样成面积为1m x 1m的块。我们对PointNet的分段版本进行训练,以预测每个块中的每个点类。每个点由XYZ、RGB和房间的归一化位置(从 0 到 1)的9维向量表示。在训练时,我们在每个块中随机抽取 4096 个点。在测试时,我们对所有点进行测试。我们遵循与 [1] 相同的协议,使用k-fold策略进行训练和测试。
我们将我们的方法与使用手工制作的点特征的基线进行比较。基线提取相同的9dim局部特征和三个额外的特征:局部点密度,局部曲率和法向量。我们使用标准MLP作为分类器。结果如表3所示,其中我们的PointNet方法明显优于基线方法。在图4中,我们显示了定性分割结果。我们的网络能够输出平滑的预测,并且对于缺失点和遮挡是鲁棒的。
基于网络的语义分割输出,我们进一步构建了一个使用连接组件进行对象提议的三维目标检测系统(详见附录)。我们在表4中与以前最先进的方法进行了比较。前一种方法是基于滑动形状方法(带有CRF后处理),在体素网格中使用svm对局部几何特征和全局房间上下文特征进行训练。我们的方法在报告的家具类别上表现出色。
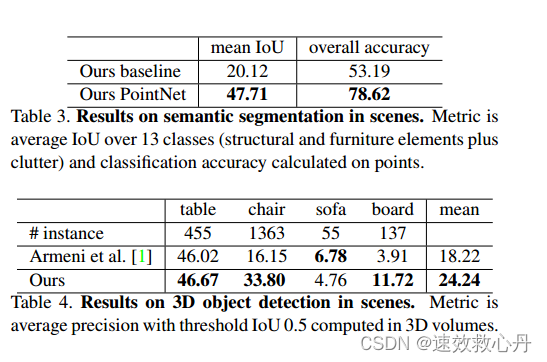
表3场景中语义分割的结果。指标是13个类别(结构和家具元素加上杂乱)的平均IoU和基于点计算的分类精度。
表4. 场景中3D目标检测的结果。指标是在3D体积中计算的阈值IoU0.5的平均精度。

图4、语义分割的定性结果。顶行是带颜色的输入点云。底行是在与输入相同的相机视点中显示的输出语义分割结果(在点上)。
5.2. 模型设计分析
在本节中,我们通过控制实验验证我们的设计选择。我们还展示了网络超参数的影响。
与其他顺序不变方法的比较 如4.2节所述,至少有三种选择来处理无序的集合输入。我们使用ModelNet40形状分类问题作为比较这些选项的测试平台,以下两个操作实验也将使用此任务。
我们比较的基线(如图5所示)包括未排序和排序点上的多层感知器(n×3阵列)、将输入点视为序列的RNN模型,以及基于对称函数的模型。我们实验的对称操作包括最大池化、平均池化和基于注意力的加权和。注意方法与[25]类似,从每个点特征预测一个标量分数,然后通过计算softmax将分数在点之间归一化。然后计算归一化分数和点特征的加权和。如图5所示,最大池化操作以较大的优势获得了最佳性能,这验证了我们的选择。
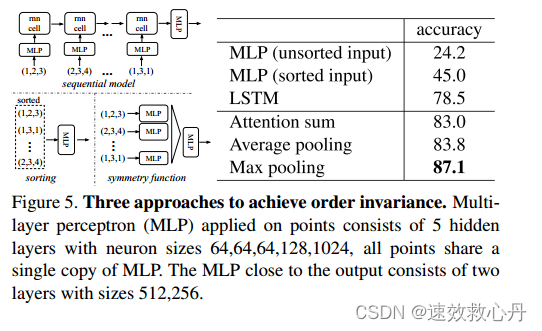
图5. 实现顺序不变性的三种方法。应用于点的多层感知器(MLP)由5个隐藏层组成,神经元大小为64、64、64、128、1024,所有点共享一个 MLP副本。靠近输出的 MLP 由大小为 512,256的两层组成。
输入和特征转换的有效性在表5中,我们展示了我们的输入和特征转换(用于对齐)的积极效果。有趣的是,最基本的架构已经取得了相当合理的结果。使用输入转换可以提高0.8%的性能。正则化损失是高维变换工作所必需的。通过结合变换和正则项,我们获得了最佳性能。
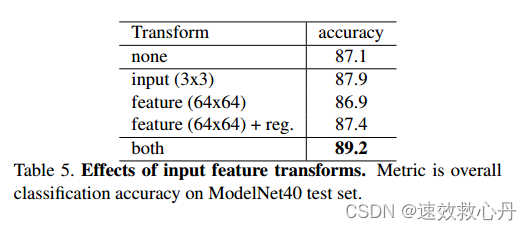
表5 输入特征变换的影响。 衡量标准是ModelNet40测试集上的整体分类准确率。
鲁棒性测试 我们展示了我们的PointNet,虽然简单有效,但对各种输入损坏具有鲁棒性。我们使用与图5的最大池化网络相同的架构。输入点被归一化为一个单位范围。结果如图6所示。
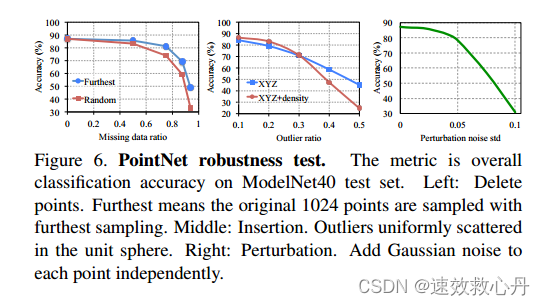
图6 PointNet稳健性测试。该指标是ModelNet40测试集上的整体分类准确率。左:删除点。最远意味着以最远采样对原始1024个点进行采样。中:插入。异常值均匀地分散在单位范围上。右:扰动。分别向每个点添加高斯噪声。
对于缺失点,当缺失点达到50%时,准确率仅比最大输入和随机输入采样分别下降了2.4%和3.8%。如果我们的网络在训练期间看到了异常点,那么它对异常点也很鲁棒。我们评估了两个模型:一个在具有(x, y, z)坐标的点上训练;另一个在(x, y, z)加上点密度。即使 20%的点是异常值,网络的准确率也超过80%。图6右侧显示了网络对点扰动的鲁棒性。
5.3 可视化PointNet
在图7中,我们可视化了一些样本形状S的临界点集CS
和上界形状NS(如在二章所述)。两个形状之间的点集将给出完全相同的全局形状特征f(S)。
从图7中我们可以清楚地看到,临界点集CS,即对最大汇集特征做出贡献的临界点集CS,概括了形状的骨架。上界形状NS表示具有与输入点云S相同的全局形状特征f(S)的最大可能点云。CS和NS反映了PointNet的鲁棒性,这意味着失去一些非关键点根本不会改变全局形状特征f(S)。
NS 通过网络转发边长为2的立方体中的所有点,选取点函数值为(h1§,h2 §,···;hK§)不大于全局形状描述符点p来构建。

图 7. 临界点和上限形状。虽然临界点共同确定给定形状的全局形状特征,但任何落在临界点集和上限形状之间的点云都会给出完全相同的特征。我们对所有图形进行颜色编码以显示深度信息。
5.4 时间和空间复杂性分析
表6总结了我们的分类PointNet的空间(网络中参数的数量)和时间(浮点运算/样本)复杂度。我们还将PointNet与先前作品中基于体积和多视图的体系结构的代表性集合进行了比较。
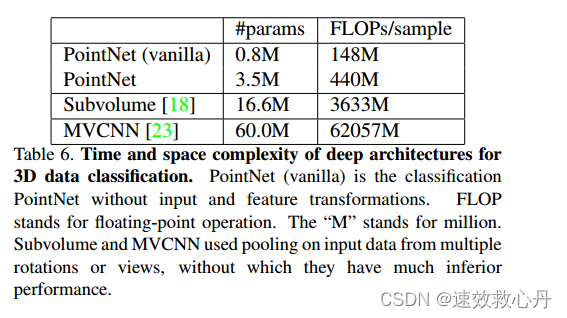
表 6. 用于3D数据分类的深度架构的时间和空间复杂度。PointNet(vanilla)是没有输入和特征转换的分类PointNet。FLOP代表浮点运算。“M”代表百万。Subvolume和MVCNN对来自多个旋转或视图的输入数据使用池化,如果没有使用池化,它们的性能要差得多。
虽然MVCNN[23]和Subvolume(3D CNN)[18]实现了高性能,但PointNet在计算成本方面的效率更高(以FLOPs/样本衡量:效率分别提高了141倍和8倍)。此外,就网络中的#param(参数少17倍)而言,PointNet比MVCNN更节省空间。此外,PointNet更具可扩展性——它的空间和时间复杂度为 O(N))——与输入点的数量呈线性关系。然而,由于卷积在计算时间中占主导地位,多视图方法的时间复杂度在图像分辨率上成正比增长,而基于体积卷积的方法随着体积大小三次增长。
经验表明,PointNet在TensorFlow上使用1080X GPU每秒能够处理超过100万个点用于点云分类(约1K个目标/秒)或语义分割(约2个房间/秒),显示出巨大的实时应用潜力.
6.结论
在这项工作中,我们提出了一种新的直接消耗点云的深度神经网络PointNet。我们的网络为许多3D识别任务提供了统一的方法,包括对象分类、部件分割和语义分割,同时在标准基准上获得与最先进的技术相当或更好的结果。我们还提供理论分析和可视化来理解我们的网络。
补充
A. Overview概述
本文档提供了额外的定量结果、技术细节和更多的定性测试示例。
在B节中,我们扩展了鲁棒性测试,以比较PointNet与VoxNet在不完全输入上的差异。在章节C中,我们提供了更多关于神经网络架构、训练参数的细节,在章节D中,我们描述了场景中的检测途径。然后,在章节E展示了PointNet的更多应用,章节F展示了更多的分析实验。第G节为我们的PointNet理论提供了一个证明。最后,我们在H部分展示了更多的可视化结果。
B.PointNet与VoxNet的比较(5.2节)
我们扩展了第5.2节鲁棒性测试中的实验,比较了PointNet和VoxNet17对输入点云中缺失数据的鲁棒性。两个网络在相同的队列测试分割上训练,以1024个数的点作为输入。对于VoxNet,我们将点云体素化为32 × 32 × 32的占用网格,并通过绕上轴随机旋转和抖动来增强训练数据。
在测试时,输入点按一定比例随机剔除。由于VoxNet对旋转很敏感,它的预测使用点云的12个可试点的平均分数。如图8所示,我们看到我们的PointNet对缺失点的鲁棒性要强得多。当一半的输入点丢失时,VoxNet的准确率会急剧下降,从86.3%下降到46.0%,差异为40.3%,而我们的PointNet的性能下降仅为3.7%。这可以通过我们PointNet的理论分析和解释来解释-它正在学习使用临界点的集合来总结形状,因此它对缺失数据非常健壮。
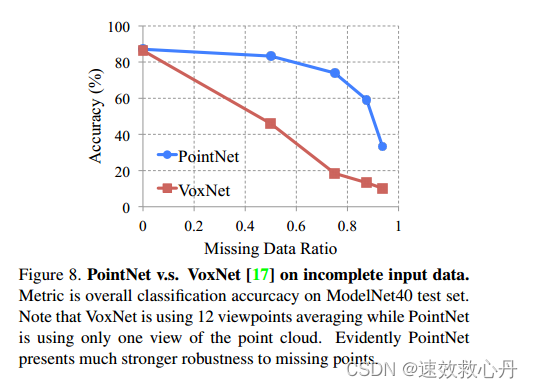
图8。PointNet vs .s. VoxNet[17]。衡量标准是在ModelNet40测试集上的总体分类精度。注意,VoxNet使用12个视点平均,而PointNet只使用点云的一个视图。显然,PointNet对缺失点具有更强的鲁棒性。
C.网络架构和训练细节(第5.1节)
PointNet分类网络由于基本架构已经在主要论文中说明,这里我们提供更多关于联合对准/转换网络和训练参数的细节。
第一个转换网络是一个mini-PointNet,它将原始点云作为输入并回归到一个3 × 3矩阵。它由一个共享的MLP(64;128;1024)网络(层输出大小为64,128,1024)在每个点上,通过点的最大池化和两个输出大小为512,256的完全连接层。输出矩阵初始化为单位矩阵。除最后一层外,所有层都包括ReLU和批处理规范化。除了输出是一个64 × 64矩阵外,第二个变换网络具有与第一个相同的体系结构。矩阵也被初始化为一个单位。将正则化损失(权值为0.001)添加到softmax分类损失中,使矩阵接近正交。
在预测类分数之前,我们在最后一个完全连接层(输出维数256)上使用保持比为0:7的dropout。批归一化的衰减率从0.5开始,逐渐增加到0.99。我们使用adam优化器,初始学习率为0.001,动量(momentum)为0.9,批大小为32。学习率每20次除以2。ModelNet上的训练需要3-6小时才能与TensorFlow和GTX1080 GPU收敛。
PointNet分割网络分割网络是对分类点网的扩展。对于每个点,将局部点特征(第二次变换网络后的输出)和全局特征(最大池化的输出)连接起来。分段网络采用无dropout。训练参数与分类网络相同。
对于形状部份分割任务,我们对基本分割网络架构(主论文图2)进行了一些修改,以达到最佳性能,如图9所示。我们添加一个表示输入类的one-hot向量,并将其与最大池化层的输出连接起来。我们还在某些层中增加神经元,并增加跳跃链接来收集不同层中的局部点特征,并将它们连接起来,形成点特征输入到分割网络中。虽然[27]和[29]独立处理每个对象类别,但由于缺乏某些类别的训练数据(数据集中所有类别的形状总数显示在第一行),我们跨类别训练我们的PointNet(但使用one-hot向量输入来指示类别)。允许公平的比较,当测试在这两个模型中,我们只预测给定特定对象类别的部份标签。
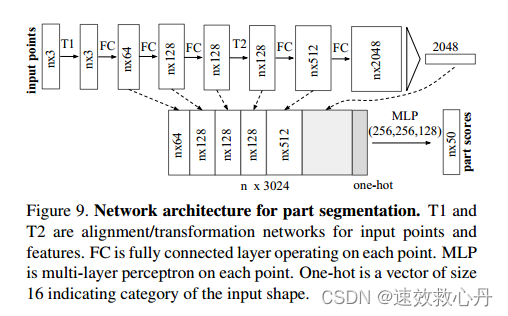
图9 部分分割的网络体系结构。T1和T2是输入点和特征的对齐/变换网络。FC是在每个点上操作的全连接层。MLP是每个点上的多层感知器。One-hot是一个大小为16的向量,表示输入形状的类别
对于语义分割任务,我们采用的架构如图2所示。
在ShapeNet部份数据集上训练模型大约需要6到12个小时,在Stanford语义分析数据集上训练大约需要半天。
基于3D CNN分割网络
在ShapeNet部分分割实验中,我们将提出的分割版本PointNet与两种传统方法以及三维体积CNN网络基线进行了比较。在图10中,我们展示了我们使用的基线3D体积CNN网络。我们将著名的3D CNN架构,如VoxNet[17]和3DShapeNets[28]推广到一个全卷积的3D CNN分割网络。

图10。基线三维CNN分割网络。该网络是完全卷积的,并预测每个体素的部分分数。
对于给定的点云,我们首先将其转换为分辨率为32 × 32 × 32的占用网格的体积表示。然后,依次进行5次三维卷积运算,每次32个输出通道,步幅为1,提取特征。每个体素的接受野是19。最后,将核大小为1 × 1 × 1的三维卷积层序列附加到计算的特征映射上,以预测每个体素的分割标签。ReLU和批处理归一化用于除最后一层以外的所有层。该网络是跨类别训练的,然而,为了与给定对象类别的其他基准方法进行比较,我们只考虑给定对象类别的输出分数。
D.检测通道的详细信息(第5.1节)
我们基于语义分割结果和我们的目标分类点网构建了一个简单的三维目标检测系统。
我们使用带有分割分数的连接分量来获得场景中的目标建议。我们从场景中的随机点开始,找到它的预测标签,并使用BFS搜索具有相同标签的附近点,搜索半径为0.2 m。如果结果聚类有超过200个点(假设在1m × 1m的区域中有4096个点样本),则聚类的边界框被标记为一个对象建议。对于每个被提议的对象,它的检测分数被计算为该类别的平均分。在评估之前,对面积/体量极小的提案进行修剪。对于桌子、椅子和沙发,围框延伸到地板上,以防腿与座位/表面分开。
我们观察到,在一些房间,如礼堂,许多物体(如椅子)彼此靠近,其中连接的组件将无法正确分割出单独的组件。因此,我们利用我们的分类网络和滑动形状方法来缓解椅子类的问题。我们为每个类别训练一个二值分类网络,并使用分类器进行滑动窗口检测。结果框被非最大抑制修剪。从连接组件和滑动形状中提出的盒子组合在一起进行最终评估。
在图11中,我们展示了目标检测的准确率-召回率曲线。我们训练了6个模型,每个模型都在5个区域进行训练,并在左侧区域进行测试。在测试阶段,每个模型都在它从未见过的区域进行测试。所有六个区域的测试结果被聚合起来生成PR曲线。
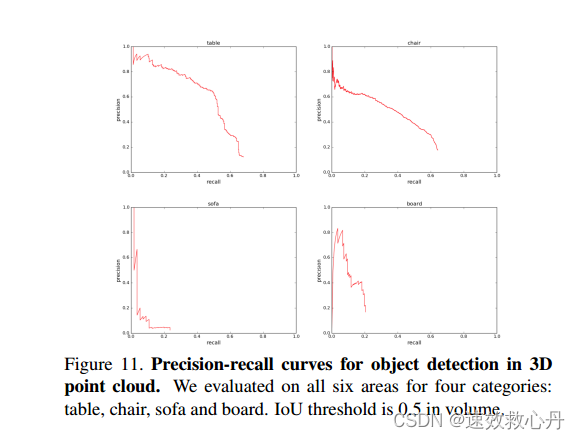
图11。三维点云目标检测的查全率曲线。我们对所有六个区域进行了四类评估:桌子、椅子、沙发和木板。IoU阈值为体积0.5。
E.更多应用(第5.1节)
点云模型检索我们的PointNet为每个给定的输入点云学习一个全局形状签名。我们期望几何上相似的形状具有相似的全局特征。在本节中,我们将在形状检索应用程序上测试我们的猜想。更具体地说,对于来自ModelNet测试分割的每个给定查询形状,我们计算其全局签名(在分数预测层之前的层的输出),并通过最近邻搜索在列车分割中检索相似的形状。结果如图12所示。
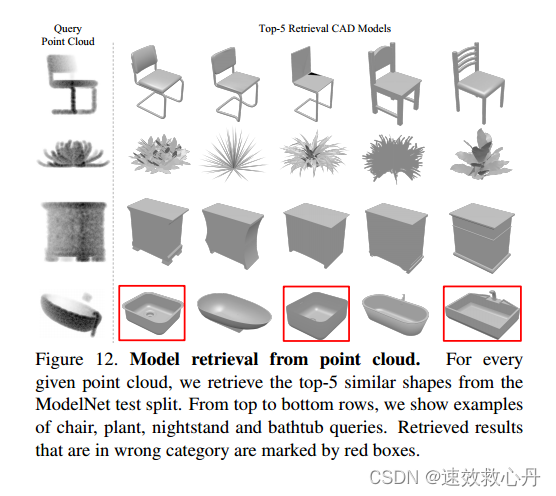
图12。点云模型检索。对于每个给定的点云,我们从ModelNet测试分割中检索前5个相似的形状。从上到下,我们展示了椅子、植物、床头柜和浴缸的查询示例。属于错误类别的检索结果用红框标记。
形状对应在本节中,我们展示了PointNet学习的点特征可以潜在地用于计算形状对应。给定两个形状,我们通过匹配全局特征中激活相同维度的点对来计算它们临界点集CS之间的对应关系。图13和图14显示了检测到的两个相似桌椅的形状对应关系。
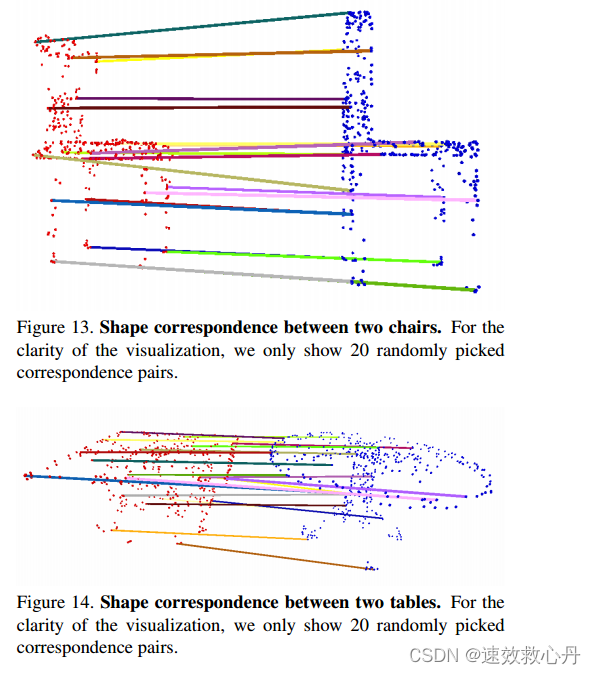
图13。两把椅子之间的形状对应。为了可视化的清晰度,我们只显示20个随机选择的对应对。
图14。两个桌子之间的形状对应关系。为了可视化的清晰度,我们只显示20个随机选择的对应对。
F.更多架构分析(第5.2节)
维度障碍和输入点数量的影响这里我们展示了我们的模型的性能变化与第一个最大层输出的大小以及输入点的数量有关。在图15中,我们看到性能随着点的增加而增长,但它在1K点左右达到饱和。最大层大小起着重要的作用,从增加层大小64 ~ 1024将导致2 ~ 4%的性能增益。这表明我们需要足够的点特征函数来覆盖三维空间,以区分不同的形状。
值得注意的是,即使使用64个点作为输入(从网格上的最远点采样获得),我们的网络也可以获得不错的性能。
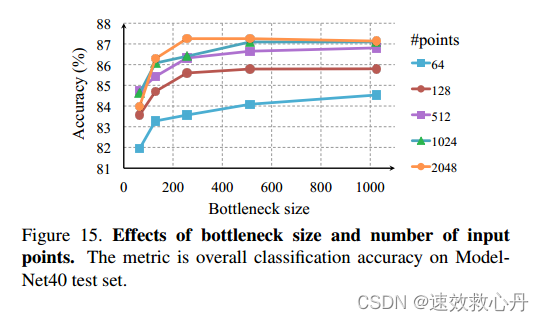
图15。瓶颈大小和输入点数量的影响。度量是ModelNet40测试集上的总体分类精度
MNIST数字分类当我们专注于3D点云学习时,一个完整性检查实验是将我们的网络应用于2D点云-像素集。
为了将MNIST图像转换为2D点集,我们对像素值进行阈值并添加像素(表示为一个点(x;Y)在图像中的坐标)值大于128的。我们使用256的集合大小。如果集合中有超过256个像素,我们随机对其进行子采样;如果更少,我们用集合中的一个像素填充集合(由于我们的Max操作,用于填充的点不会影响结果)。
如表7所示,我们比较了一些基线,包括多层感知器(将输入图像视为有序向量)、RNN(将输入视为从像素(0,0)到像素(27,27)的序列)和vanilla CNN。虽然在MNIST上表现最好的模型仍然是设计良好的cnn(达到低于0.3%的错误率),但有趣的是,我们的PointNet模型可以通过将图像视为2D点集来实现合理的性能。
正态估计
在PointNet的分割版本中,为了给局部点提供上下文,将局部点特征和全局特征拼接在一起。然而,语境是否通过这种连接学习尚不清楚。在这个实验中,我们通过展示我们的分割网络可以被训练来预测点法线来验证我们的设计,这是一个由点的邻域决定的局部几何属性。
我们以监督的方式训练我们的分割点网的修改版本,以回归到真点法线。我们只是改变我们的分割点网的最后一层来预测每个点的法向量。我们用余弦距离的绝对值作为损失。
图16比较了我们的PointNet法线预测结果(左列)和从网格计算的真实法线(右列)。我们观察到一个合理的正常重建。我们的预测比包括在某些区域翻转法线方向的基本事实更平滑和连续。
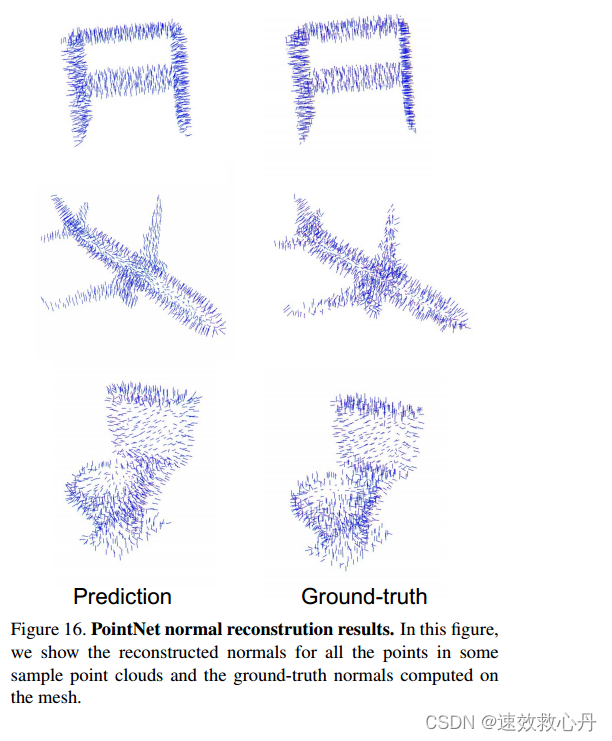
图16。顶点网法向重建结果。在这个图中,我们展示了一些样本点云中所有点的重建法线和在网格上计算的真实法线。
分割的鲁棒性正如第5.2节和B节所讨论的,我们的PointNet对分类任务的数据损坏和缺失点不太敏感,因为全局形状特征是从给定输入点云的临界点集合中提取的。在本节中,我们将展示鲁棒性也适用于分割任务。基于点特征和学习到的全局形状特征相结合的方法预测每点部分标签。在图17中,我们展示了给定输入点云S(最左边的列)、临界点集CS(中间的列)和上界形状NS的分割结果。
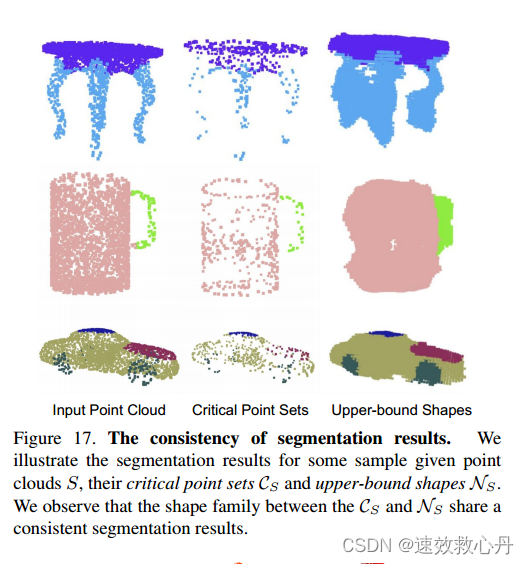
图17。分割结果的一致性。我们给出了给定点云S、临界点集CS和上界形状NS的分割结果。我们观察到CS和NS之间的形状族具有一致的分割结果。
网络推广到看不见的形状类别在图18中,我们可视化了来自ModelNet或ShapeNet中不存在的未见类别(脸、房子、兔子、茶壶)的新形状的临界点集和上限形状。结果表明,所学习的逐点函数具有可泛化性。然而,由于我们主要训练具有大量平面结构的人造物体,因此在新类别中重构的上界形状也包含了更多的平面。
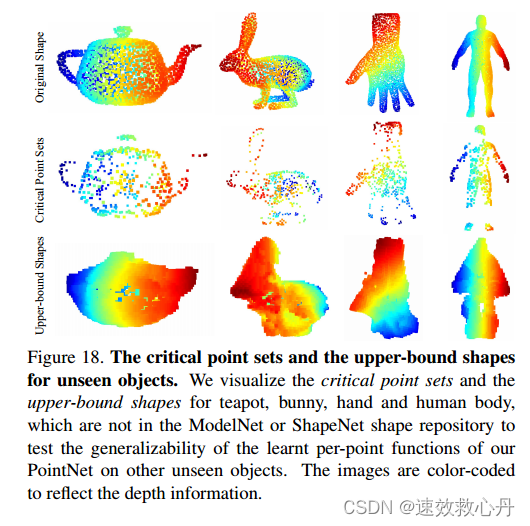
图18.不可见物体的临界点集和上界形状。我们可视化了茶壶、兔子、手和人体的临界点集和上限形状,这些都不在ModelNet或ShapeNet形状存储库中,以测试PointNet学习到的每个点函数在其他看不见的物体上的泛化性。图像用颜色编码以反映深度信息。
G.定理证明(第4.3节)
略
H. 更多的可视化
分类可视化我们使用t-SNE[15]将我们的分类PointNet中的点云全局签名(1024-dim)嵌入到二维空间中。ModelNet 40测试分割形状的嵌入空间如图20所示。相似的形状根据它们的语义类别聚在一起。

图20。学习形状全局特征的二维嵌入。我们使用t-SNE技术来可视化ModelNet40测试分割中学习到的形状的全局特征
分割可视化
我们在完整的CAD模型和模拟的Kinect部分扫描上都给出了更多的分割结果。我们还通过错误分析来可视化失败案例。图21和图22显示了完整CAD模型及其模拟Kinect扫描的更多分割结果。图23展示了一些失败案例。请阅读错误分析的标题。
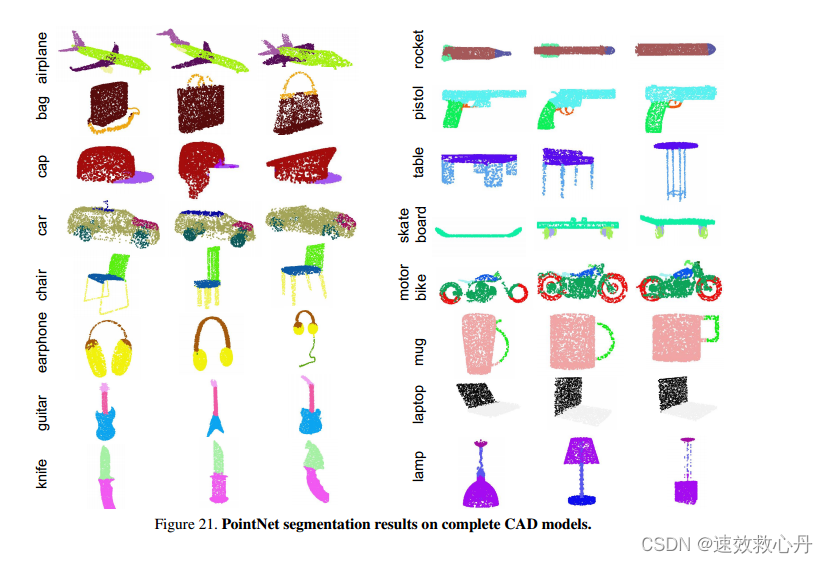
图21。对完整CAD模型的点网分割结果。

图22。点网分割结果模拟Kinect扫描。
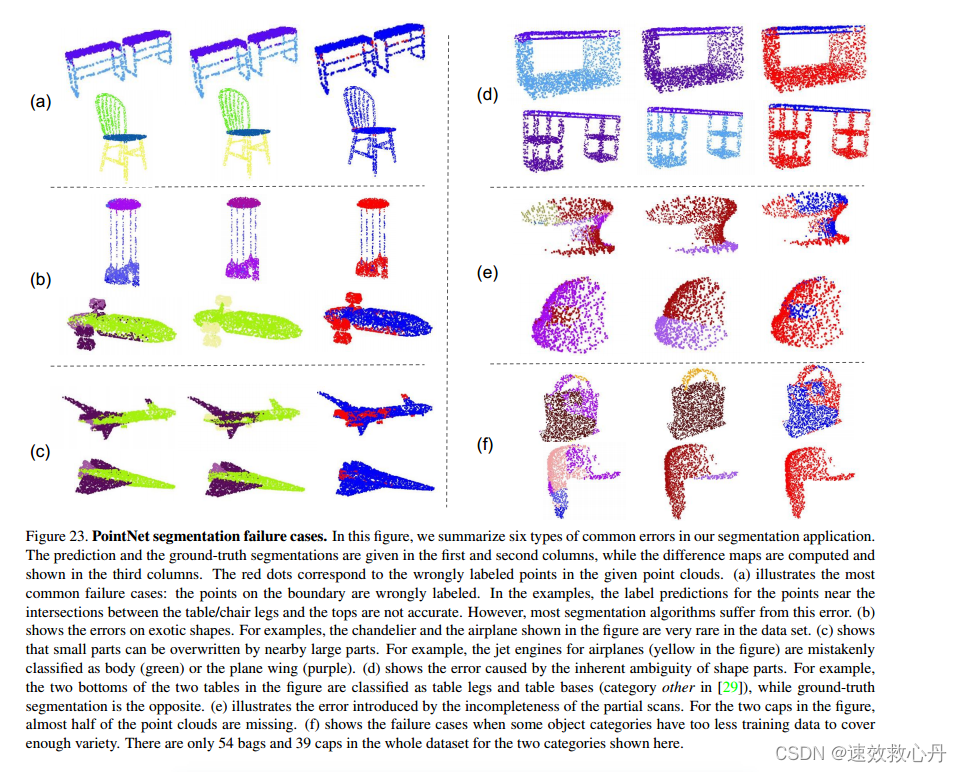
图23。点网分割失败案例。在这个图中,我们总结了分割应用程序中的六种常见错误。
第一列和第二列给出了预测和ground-truth分割,而第三列计算并显示了差分图。红点对应于给定点云中被错误标记的点。(a)说明了最常见的失效情况:边界上的点被错误地标记。在示例中,对于桌子/椅子腿和顶部之间的交叉点附近的点的标签预测是不准确的。然而,大多数分割算法都存在这个错误。(b)显示了奇异形状的误差。例如,图中的吊灯和飞机在数据集中是非常罕见的。?表明小的部分可以被附近的大部分覆盖。例如,飞机的喷气发动机(图中黄色)被错误地分类为机身(绿色)或飞机机翼(紫色)。(d)为形状零件固有模糊性引起的误差。例如,图中两张桌子的两个底部被分类为桌腿和桌座(other类见[29]),而ground-truth segmentation则相反。(e)说明了局部扫描不完整所带来的误差。对于图中的两个帽,几乎一半的点云丢失了。(f)显示了当某些对象类别的训练数据太少而无法涵盖足够的种类时的失败情况。在这里显示的两个类别中,整个数据集中只有54个袋子和39个帽子。
场景语义解析可视化
我们在图24中给出了语义解析的可视化,其中我们显示了两个办公室和一个会议室的语义分割和目标检测的输入点云、预测和地面真值。这个区域和房间在训练集中是看不见的。

图24。语义分割和对象检测的例子。第一行是输入点云,为了清晰,墙壁和天花板被隐藏起来。第二行和第三行是对点的语义分割的预测和基础真值,其中属于不同语义区域的点的颜色不同(椅子为红色,桌子为紫色,沙发为橙色,木板为灰色,书柜为绿色,地板为蓝色,窗户为紫色,梁为黄色,柱为洋红色,门为卡其色,杂乱物为黑色)。最后两行是带边界框的对象检测,其中预测框来自基于语义分割预测的连接组件。
点函数可视化
我们的分类PointNet为每个点计算K(我们在这个可视化中取K = 1024)维度点特征,并通过最大池化层将所有每个点的局部特征聚合到一个K-dim向量中,形成全局形状描述符。
为了更深入地了解学习到的逐点函数h’s检测到什么,我们将图19中给出高逐点函数值f(pi)的点pi’s可视化。这个可视化清晰地显示了不同的点函数学习检测不同区域的点,不同的形状分散在整个空间中。

图19所示。点函数可视化。对于每个点函数h,我们计算原点处直径为2的立方体中所有点p的值h§,该立方体在空间上覆盖了我们在训练PointNet时将输入形状归一化的单位球体。在这张图中,我们将h§ > 0:5的所有点p可视化,并使用由体素亮度颜色编码的函数值。我们随机选择15个点函数并可视化它们的激活区域。
注:文中的内容图片皆翻译来自于论文《PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation》
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!