BP神经网络原理及其实现

BP神经网络原理及其实现

摘要：

本文围绕BP神经网络原理及其算法实现进行论述。
首先简单介绍人工神经元的概念；
基于此，论述BP神经网络算法的原理及公式推导过程，为了便于理解BP网络工作过程，基于公式推导过程，重点论述正向传播与反向传播过程，；
并给出其中一些关键概念，如激活函数意义等；
最后，利用MatLab工具，给出BP神经网络的应用案例。

1 背景及概念

感知器（Perceptron）

感知器由Frank Roseblatt 于1957年提出，是一种广泛使用的线性分类器。感知器可谓是最简单的人工神经网络，只有一个神经元。

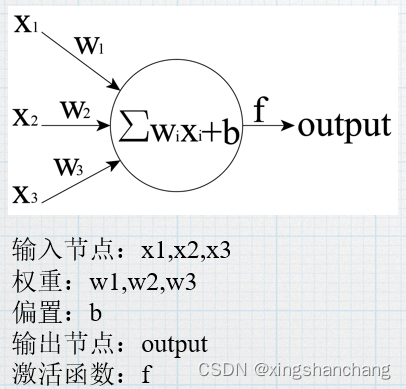
人工神经元

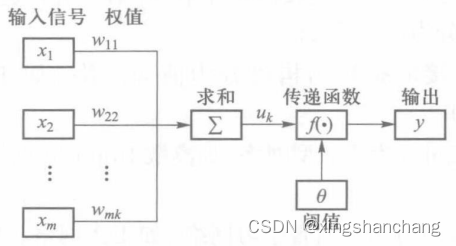
人工神经元是人工神经网络的基本信息处理单元,它是对生物神经元的简化和模拟。人工神经元的简化模型如图所示,其中,xi为输入信号,theta/θ为阈值,权值w,表示连接的强度, y为输出信号。

2 BP神经网络算法

2.1 简介

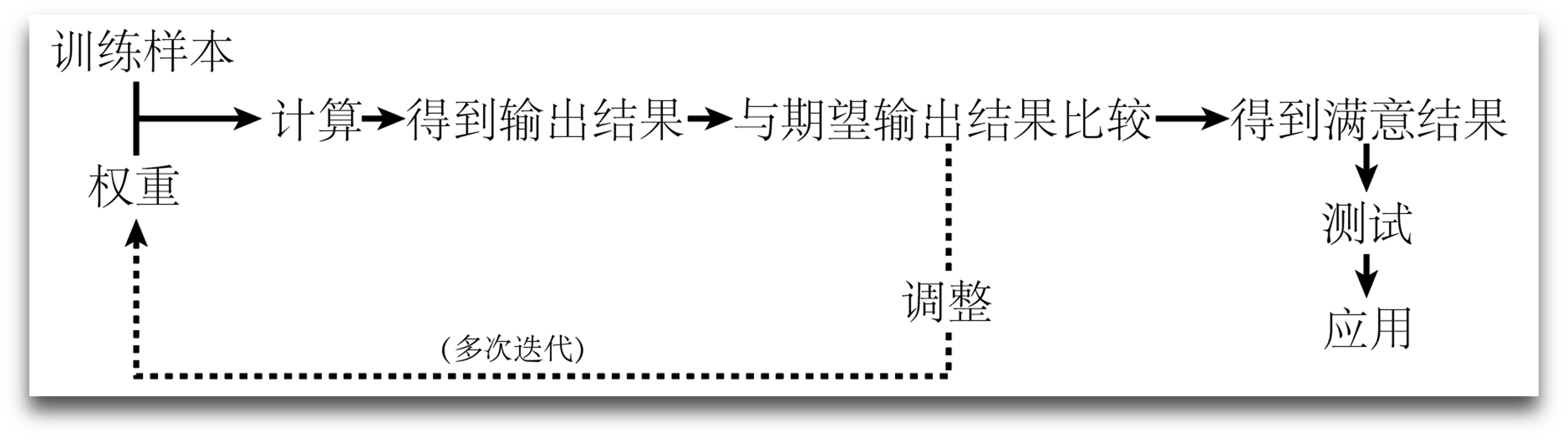
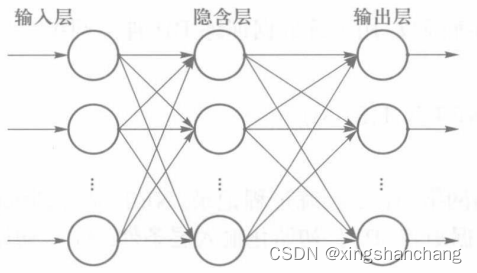
BP人工神经网络由输入层、隐含层和输出层3层组成,其结构如图所示。在结构确定之后,要通过输人和输出样本集对网络进行训练,即通过一边向后传递误差一边修正误差的方法来不断地调节网络参数(权值和阈值),以使网络实现或逼近所希望的输入、输出映射关系。

BP网络的学习过程分为以下两个阶段:

• 第1个阶段是正向传播过程,输入已知学习样本,通过设置的网络结构和前一次迭代的权值和阈值,从网络的第1层向后计算各神经元的输出。
• 第2个阶段是反向传播过程,逐层计算实际输出与期望输出之间的差值,据此对各权值和阈值进行修改使误差信号趋向最小。

以上两个过程反复交替,直至收敛为止。由于误差逐层往回传递,用来修正层与层之间的权值和阈值,所以称该算法为误差反向传播算法,这种误差反向传播学习算法可以推广到有若干个中间层的多层网络,因此这种多层网络常称为BP网络。标准的BP算法学习规则是一种梯度下降学习算法,其权值的修正是沿着误差性能函数梯度的反方向进行的。

2.2 算法原理

BP (Back Propagation) 神经网络的核心步骤如下。其中，实线代表正向传播，虚线代表反向传播。

2.3 公式🔺

bp神经网络主要由三部分组成，分别是前向传播，反向传播，测试模型。
其中前向传播主要是计算模型当前的预测结果，反向传播是对模型进行修正得到能达到预测效果的模型，测试模型是看我们最后通过反向传播得到的模型能否识别出我们想要的分类。

搞清楚下面这个公式推导过程，就清楚了BP算法的关键。

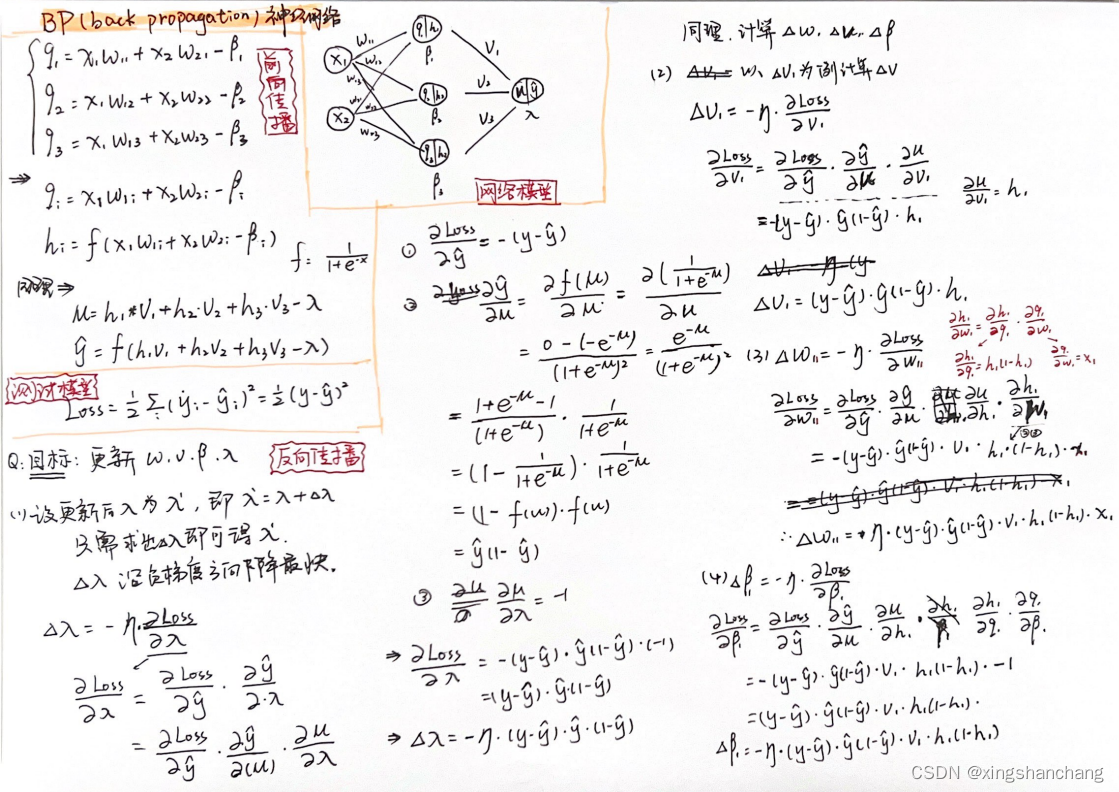
注：这里公式本质就是链式求导法则。上述推导过程中，为了便于理解，采用标量的形式推导；实际中，为了方便写作，可以采用向量方式推导。

这里有一个英文的逐步推导过程案例：http://galaxy.agh.edu.pl/~vlsi/AI/backp_t_en/backprop.html
写的还行，但是不够直观。

3 补充讨论

3.1 激活函数

在深度学习网络中，我们经常可以看到对于某一个隐藏层节点的激活值计算一般分为两步，如下图：

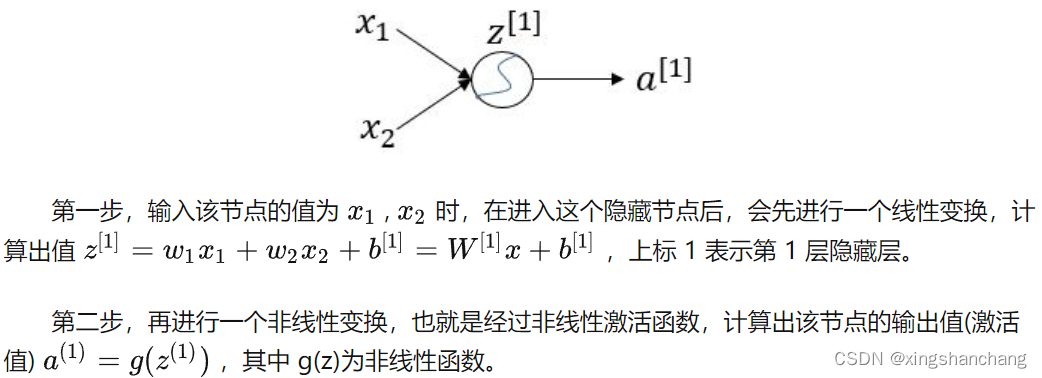
• 那么问题来了，这个激活函数到底有什么用呢，可不可以不加激活函数呢？

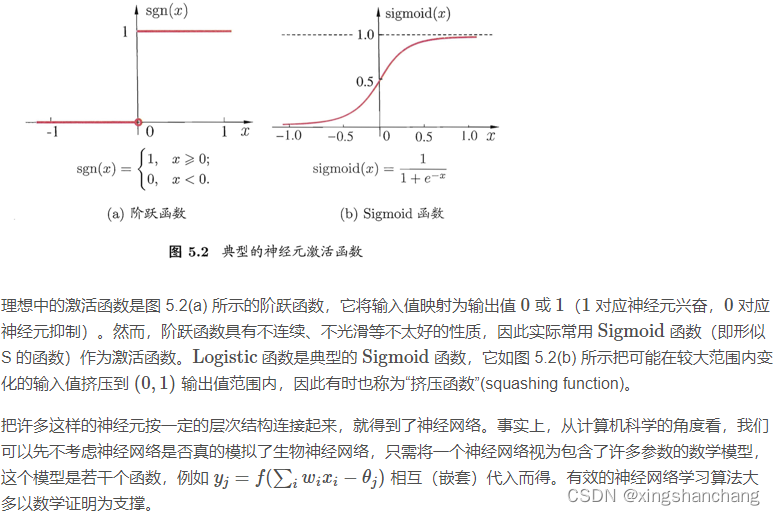
什么是激活函数？

激活函数是神经网络中极其重要的概念。它们决定了某个神经元是否被激活，这个神经元接受到的信息是否是有用的，是否该留下或者是该抛弃。激活函数的形式如下：

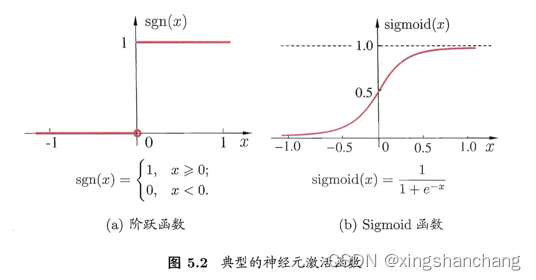
激活函数是我们对输入做的一种非线性的转换。转换的结果输出，并当作下一个隐藏层的输入。

如果没有激活函数会怎样？

1、首先对于y=ax+b 这样的函数，当x的输入很大时，y的输出也是无限大/小的，经过多层网络叠加后，值更加膨胀的没边了，这显然不符合我们的预期，很多情况下我们希望的输出是一个概率。

2、线性变换太简单（只是加权偏移），限制了对复杂任务的处理能力。没有激活函数的神经网络就是一个线性回归模型。激活函数做的非线性变换可以使得神经网络处理非常复杂的任务。例如，我们希望我们的神经网络可以对语言翻译和图像分类做操作，这就需要非线性转换。同时，激活函数也使得反向传播算法变的可能。因为，这时候梯度和误差会被同时用来更新权重和偏移。没有可微分的线性函数，这就不可能了。

3、结论：可以用线性激活函数的地方一般会是输出层。

常用的激活函数有哪些？

在深度学习中，常用的激活函数主要有：sigmoid函数，tanh函数，ReLU函数、Leaky ReLU函数。

数据归一化

• 什么是归一化？
  – 将数据映射到[0, 1]或[-1, 1]区间或其他的区间。

• 为什么要归一化？
  – 输入数据的单位不一样，有些数据的范围可能特别大，导致的结果是神经网络收敛慢、训练时间长。
  – 数据范围大的输入在模式分类中的作用可能会偏大，而数据范围小的输入作用就可能会偏小。
  – 由于神经网络输出层的激活函数的值域是有限制的，因此需要将网络训练的目标数据映射到激活函数的值域。例如神经网络的输出层若采用S形激活函数，由于S形函数的值域限制在(0,1)，也就是说神经网络的输出只能限制在(0,1)，所以训练数据的输出就要归一化到[0,1]区间。
  – S形激活函数在(0,1)区间以外区域很平缓，区分度太小。例如S形函数f(X)在参数a=1时，f(100)与f(5)只相差0.0067。

• 归一化算法
  – y = ( x - min )/( max - min )
  – y = 2 * ( x - min ) / ( max - min ) -1

4 案例及其说明

4.1 newff（）函数使用方法

net = newff(data,label,[8,8],{'tansig','purelin'},'trainlm')

（1）输入参数详细介绍：

data：训练时网络的输入数据。newff函数会把data的一列当作一个样本，如果你的数据集是一行当作一个样本，记得将你的输入数据矩阵转置data.‘
label：对应输入数据的标签，也可以看作真实输出。同上，newff函数会把label的一列当作一个样本的标签，如果你的数据集是一行当作一个样本，记得将你的输入数据矩阵转置label.‘
[8,8]：用于确定神经网络隐藏层的层数以及每层的神经单元个数。[8,8]就表示该网络包含两个隐藏层，每个隐藏层有8个神经单元
{‘tansig’,‘purelin’}：表示个隐藏层所用的激活函数。{‘tansig’,‘purelin’}表示第一层用tansig激活函数，是一种S型激活函数；第二次用purelin激活函数，是一种线性型激活函数。常见的激活函数如下：

 logsig：对数S型函数
 tansig：正切S型函数
 purelin：线性型函数

‘trainlm’：确定训练函数，默认为trainlm函数，该方法需要占用更大的存储空间，使用了Levenberg-Marquardt算法,对于中等规模的BP神经网络有最快的收敛速度。由于其避免了直接计算赫赛矩阵,从而减少了训练中的计算量,但需要较大内存量，随着神经元的增多，训练时间增加较大。常见的训练方法如下：

 traingd：梯度下降算法
 traingdm：带动量的梯度下降算法
 traingda：学习率变化的梯度下降算法
 traingdx：学习率变化带动量的梯度下降算法
 trainrp：RPROP算法，内存需求小，适用于大型网络
 trainoss：OneStep Secant Algorithm，计算量与内存需求较小，适用于大型网络

（2）其他参数设置：

net.trainParam.goal = 1e-3 ：确定目标值为0.001，到此值时训练停止
net.trainFcn=‘trainlm’ ：确定训练函数trainlm。如果newff（）中设置了，后续可以用不设置
net.trainParam.lr = 0.1 ： 确定学习率为0.1
net.divideFcn = ‘’ ：取消newff（）默认再次划分操作。newff（）默认将训练集重新划分6：2：2，训练集：测试集：验证集，在训练过程中会自动在某一处停止，我认为是为了防止过拟合吧，实践中在新训练集损失和新验证集损失下降不明显，且验证损失有上升的趋势时停止。对于数据本来就少的情况，建议取消划分。
net.trainParam.epochs = 1000 ：训练最大迭代次数
net.trainParam.min_grad =1e-24 ： 最小梯度值，到此值时训练停止

4.2. 用newff（）搭建一个简单的BP神经网络

% I. 清空环境变量
clear all
clc

% II. 训练集/测试集产生
p_train = rand(3,4);%按列看，4个样本，每个样本维度为3
t_train = rand(1,4);%按列看，4个样本标签，每个标签维度1维

p_test = rand(3,4);
t_test = rand(1,4);

% III. BP神经网络创建、训练及仿真测试
% 1. 创建网络，[3]意思为网络含有一个隐藏层，每层有3个单元
net = newff(p_train,t_train,[3],{'tansig','purelin'});

% 2. 设置训练参数
net.trainParam.epochs = 1000;%训练批次
net.trainParam.goal = 1e-12;%训练目标，误差小于1e-12即结束训练
net.trainParam.lr = 0.01;%设置学习率
%另外也可以设置其他训练参数，可看newff()函数介绍手册

% 3. 训练网络
net = train(net,p_train,t_train);

% 4. 仿真测试
t_sim = sim(net,p_test);%预测结果
error = t_test - t_sim;%误差

4.3 newff函数新旧版本差异

新版newff

Syntax

• net = newff(P,T,[S1 S2…S(N-l)],{TF1 TF2…TFNl}, BTF,BLF,PF,IPF,OPF,DDF)

Description

• newff(P,T,[S1 S2…S(N-l)],{TF1 TF2…TFNl}, BTF,BLF,PF,IPF,OPF,DDF) takes several arguments

参数	含义
P	R x Q1 matrix of Q1 sample R-element input vectors
T	SN x Q2 matrix of Q2 sample SN-element target vectors
Si	Size of ith layer, for N-1 layers, default = [ ].(Output layer size SN is determined from T.)
TFi	Transfer function of ith layer. (Default = ‘tansig’ for hidden layers and ‘purelin’ for output layer.)
BTF	Backpropagation network training function (default = ‘trainlm’)
BLF	Backpropagation weight/bias learning function (default = ‘learngdm’)
IPF	Row cell array of input processing functions. (Default = {‘fixunknowns’,‘removeconstantrows’,‘mapminmax’})
OPF	Row cell array of output processing functions. (Default = {‘removeconstantrows’,‘mapminmax’})
DDF	Data divison function (default = ‘dividerand’)

新版newff与旧版newff调用语法对比

• Example1
  比如输入input（61000），输出output为（41000），那么
  旧版定义：net=newff(minmax(input),[14,4],{'tansig','purelin'},'trainlm');
  新版定义：net=newff(input,output,14,{'tansig','purelin'},'trainlm');
• Example2
  比如输入input（61000），输出output为（41000），那么
  旧版定义：net=newff(minmax(input),[49,14,4],{‘tansig’,‘tansig’,‘tansig’},‘traingdx’);
  新版定义：net=newff(input,output, [49,14], {‘tansig’,‘tansig’,‘tansig’},‘traingdx’);

4.4 旧版newff使用方法在新版本中使用

提示：旧版本定义的newff虽也能在新版本中使用，但会有警告，警告如下：

Warning: NEWFF used in an obsolete way.
In obs_use at 18
In newff>create_network at 127
In newff at 102
See help for NEWFF to update calls to the new argument list.

4.5 新版newff与旧版newff使用的训练效果对比

旧版本：旧用法训练次数多，但精度高
新版本：新用法训练次数少，但精度可能达不到要求

造成上述原因是：
程序里面的权值、阈值的初始值是随机赋值的，所以每次运行的结果都会不一样，有好有坏。

你可以把预测效果不错的网络的权值和阈值作为初始值。
也就是说，可以通过设计一个循环结构，选选出来最优的权值和阈值。
对于选择隐藏层的神经元的数目，也可以采用改思路，案例：

t=[0 1;0 1;0 1;0 1;0 1;0 1;0 1;0 1;0 1;1 1;1 1;1 1;1 1;1 1;1 1;1 1;1 1;1 1];
t=t';
s= 32:41;
for i=1:10
    net=newff(minmax(gytest),[s(i),2],{'tansig','logsig'},'traingdx');
    net.trainParam.epochs =1000; %训练最大迭代次数
    net.trainParam.lr = 0.1; %确定学习率为0.1
    net.trainParam.goal = 0.001; %确定目标值为0.001，到此值时训练停止
    %net.trainParam.min_grad =1e-24 ： 最小梯度值，到此值时训练停止
    %net.trainFcn=‘trainlm’ ：确定训练函数trainlm。如果newff（）中设置了，后续可以用不设置
    
    net=train(net,gytest,t);           
    %gytest为归一化后训练样本，t为训练样本的目标输出
    
    y=sim(net,gytest);
    y=y-t;
    y1(i)=norm(y);
    %n = norm(v) 返回向量 v 的欧几里德范数。此范数也称为 2-范数、向量模或欧几里德长度。
end

5 参考文献

• BP神经网络（算法整体思路及原理+手写公式推导）：https://blog.csdn.net/qq_47233366/article/details/119890758
• newff函数使用方法：https://blog.csdn.net/weixin_44248258/article/details/122064776