12.15_黑马数据结构与算法笔记Java
目录
144 avl树 balance


?新增的时候不需要加=号,删除的时候需要。为了解决以上的例子。
145 avl树 put


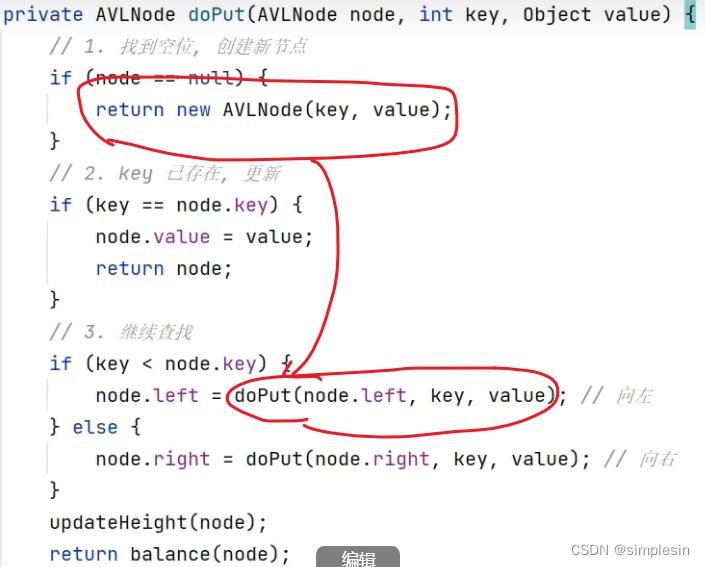
昨天做了很多伪递归的演示,遂我们知道,这里return回来的东西就是doPut()这东西的返回值,这个return回来的东西要和树建立连接,因为是在node的左边进行查找,那自自然就是连接node的左手。?
146 avl树 remove


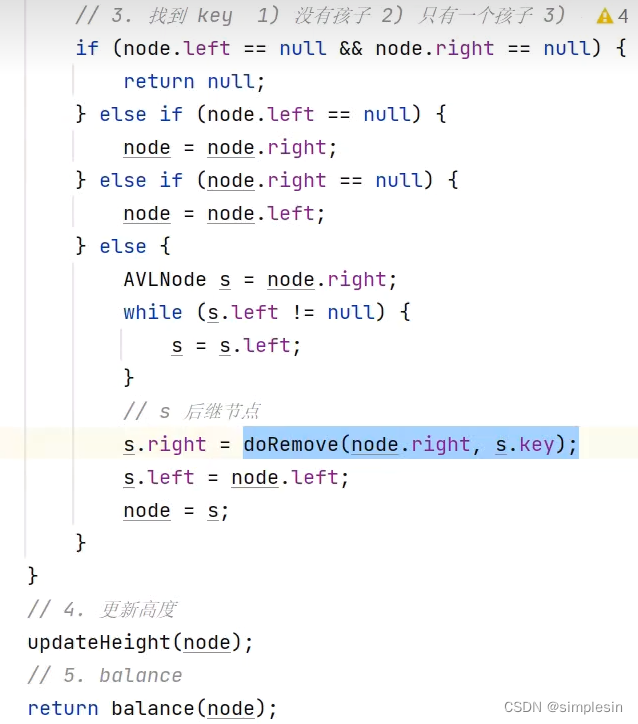
147 红黑树 概述

我们什么时候考虑null值,就是发现,有左孩子却没有右孩子的时候,要把另外一个兄弟也加进来。?


小妙招:
如果叶子节点,就是最下面的这个点如果是黑色的,一定要成对出现,如果是红色的,那一定是对的。?


parent.isLeftChild:父亲是不是爷爷的左孩子。?


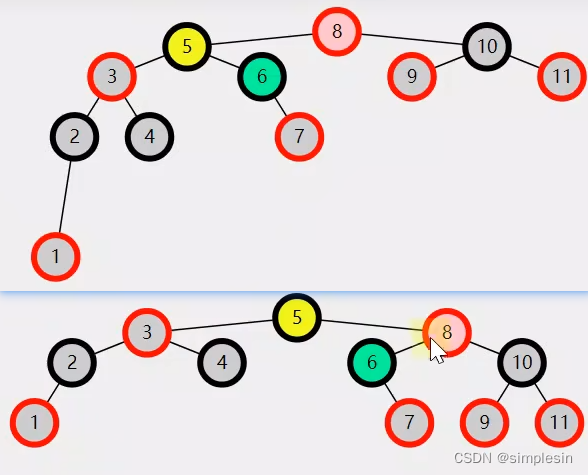
?


148 红黑树 put case1-3






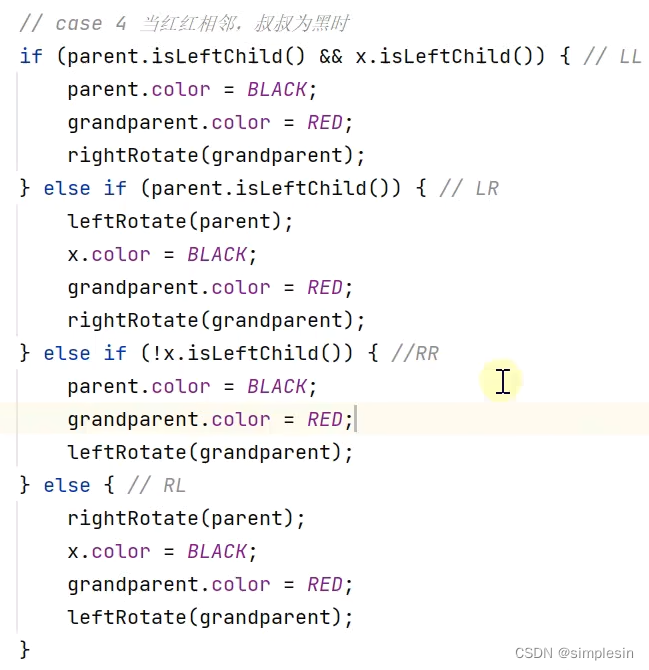
149 红黑树 put case4

150 红黑树 remove case0-1
准备工作:



李代桃僵方法:不改变其他东西,只改变5和6的值。这样子可以简化代码。
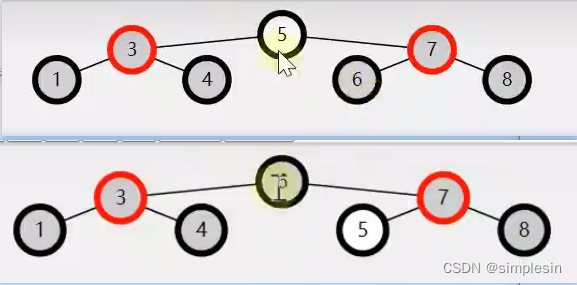
删除的是两个孩子

删除的是没有孩子或者一个孩子,并且删除的是根节点

151 红黑树 remove case2
删除的是没有孩子,且不是根节点的。
那就让它的父母指向null,然后设置它自己的新父母为null,有利于垃圾回收。这说明没有人引用它了,他就会自动被清理掉。

?删除的是有一个孩子的,且不是根节点的。
倒数第二行的代码,几个连等null的代码的意思是:我让要删除的元素和所有人脱掉关系,因此有助于垃圾回收。

现在要考虑平衡的问题了:
删黑色要考虑平衡问题,删红色不需要?
?
152?红黑树 remove case3

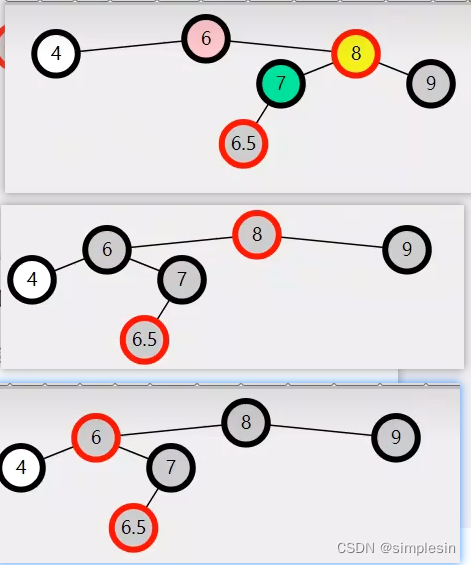
?

后面的再次递归,是将case3变成case4
153?红黑树 remove case4

几个例子
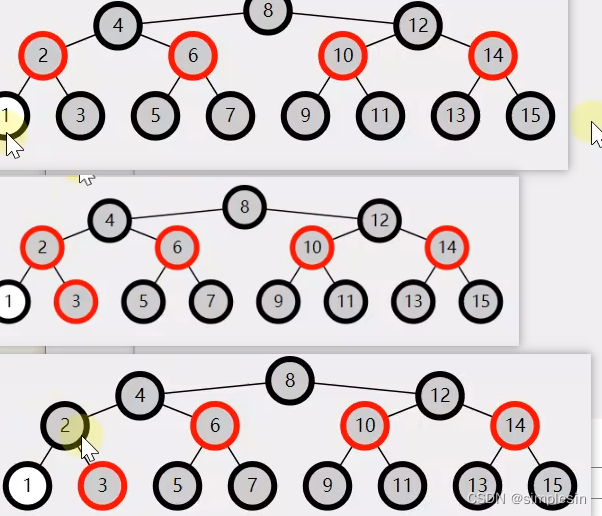

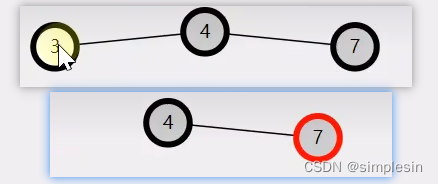

?
154?红黑树 remove case5





155?红黑树 remove 演示
156 B树 历史

157 B树 特性
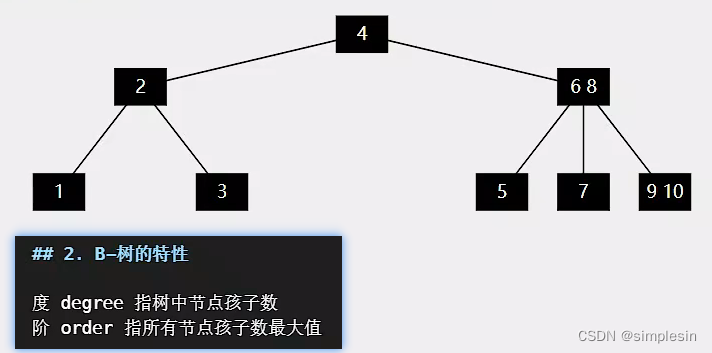
4有两个孩子,也就是度为2?

关键字数就是key,可以有多个。从孩子数推导到关键字数?
158?B树 节点类1

159?B树 节点类2
怎么去看红色框框?
如图举例子,如果要查找的是18,keys【3】(20)>18,说明在第二行
如果要查找的是30,keys【5】(30)已然超过了第一行,说明在第二行

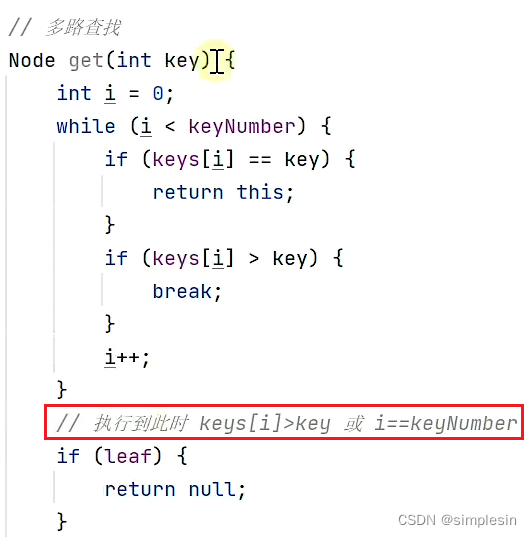

如果是非叶子的情况,则调用孩子来查找,因为比如说那个序号5,第一行是找不到序号5的,但是第二行是有序号5的。?
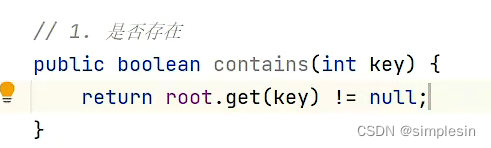
160?B树 contains

为什么在B树中,2倍树中节点最小度数-1等于最大key数目
在B树中,2倍树中节点的最小度数-1等于最大key数目是因为B树的定义和性质决定的。
B树是一种多路搜索树,它的每个节点可以包含多个子节点和关键字。在B树中,每个节点的关键字数量要满足一定的条件,即最小度数-1到2倍最小度数-1之间。同时,每个节点的子节点数量比关键字数量多1。
当节点的最小度数为t时,根据B树的性质,每个节点至少包含t-1个关键字和最多2t-1个关键字。而2倍树中的节点的最小度数为2t,因此最小度数-1就等于t-1,最大key数目就等于2t-1。
因此,在B树中,2倍树中节点的最小度数-1等于最大key数目是由B树的定义和性质决定的。
最小度数是啥
在B树中,最小度数是指一个节点中包含的最少子节点数。在B树中,每个节点都包含一个关键字和对应的子节点,最小度数规定了节点中子节点的最少数量。对于一个最小度数为t的B树,每个非根节点必须至少包含t个子节点,而根节点至少包含2个子节点。
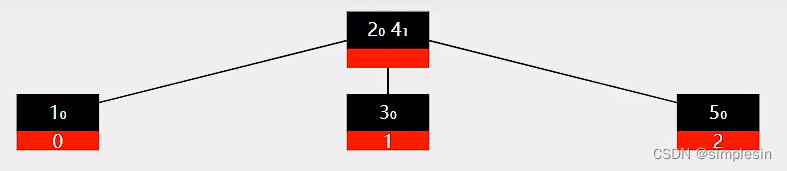
root就是一个普通的节点?
161 B树 put

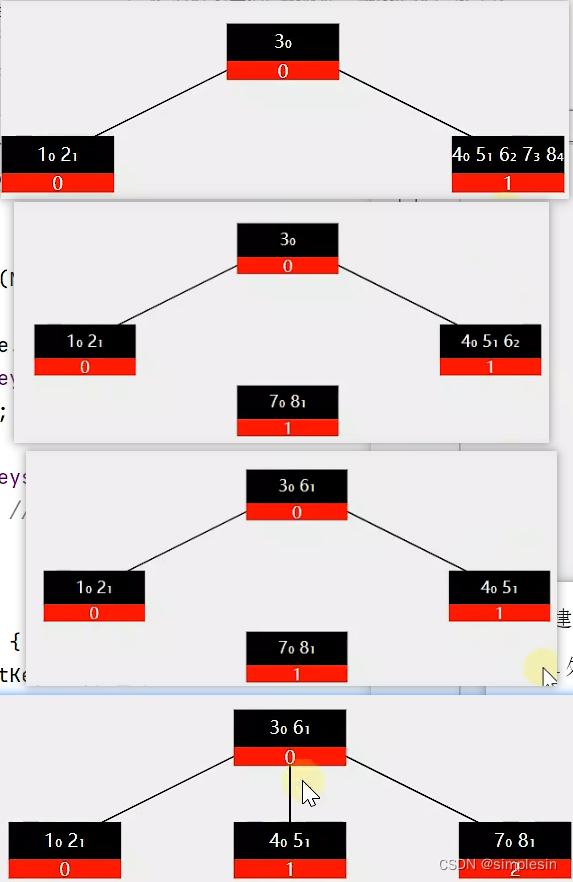
162 B树 split 分析

再举一个例子:

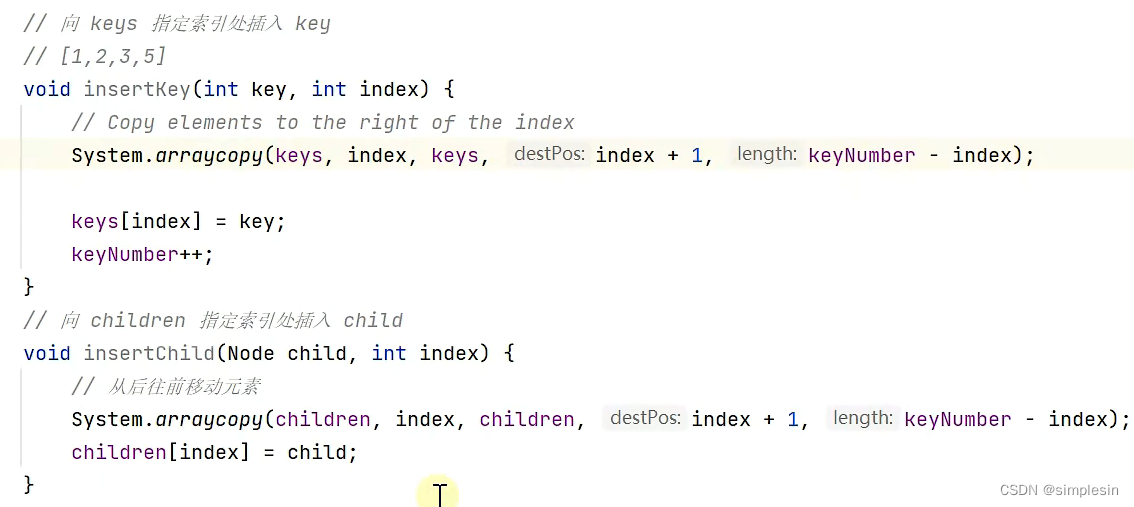
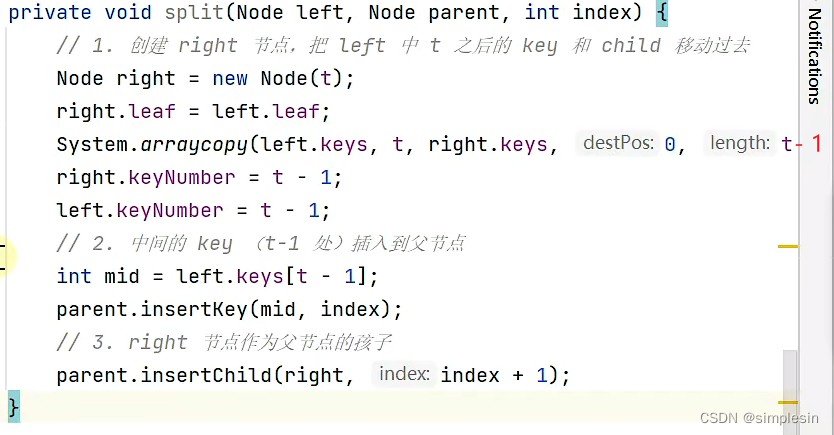
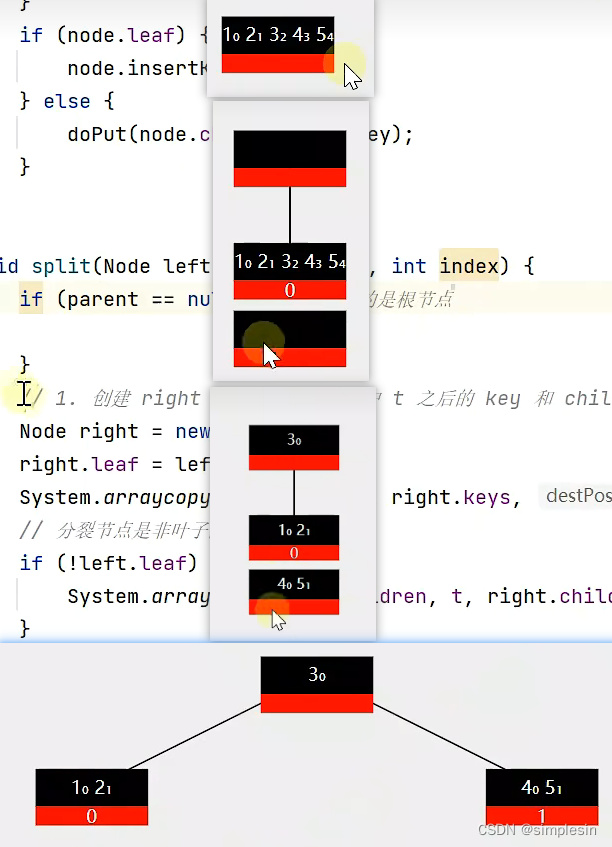
163 B树 split 实现
boolean leaf = true;right.leaf = left.leaf;什么意思?
首先,"boolean leaf = true;" 是一个声明语句,它创建了一个名为leaf的布尔变量,并将其赋值为true。这表示leaf变量是一个布尔类型的变量,它的值为true,即表示为叶子节点。
接着是"right.leaf = left.leaf;" 这是一个赋值语句,它将right节点的leaf属性设置为和left节点的leaf属性相同。这意味着right节点的leaf属性将被设置为和left节点相同的布尔值。这可能是在处理树的数据结构时,用来设置节点的属性,以便在树的遍历或搜索过程中进行判断和处理。
index:在那行,你是第几个。
164 B树 split 非叶子和根


 ?
?
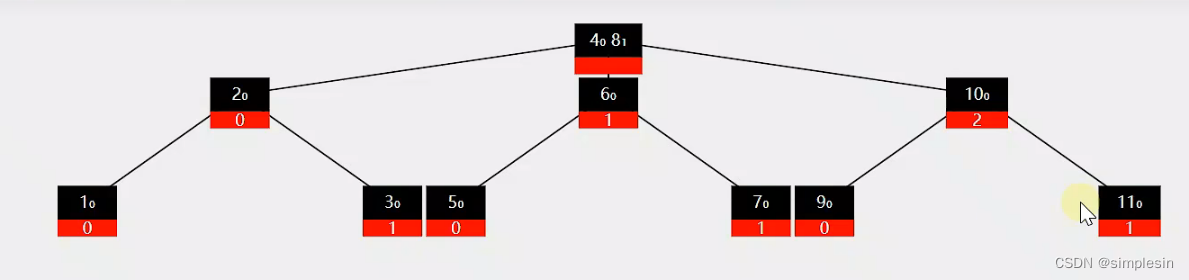
第二种情况:根节点


165 B树 split 测试
两种测试方式:
1.debug
2.

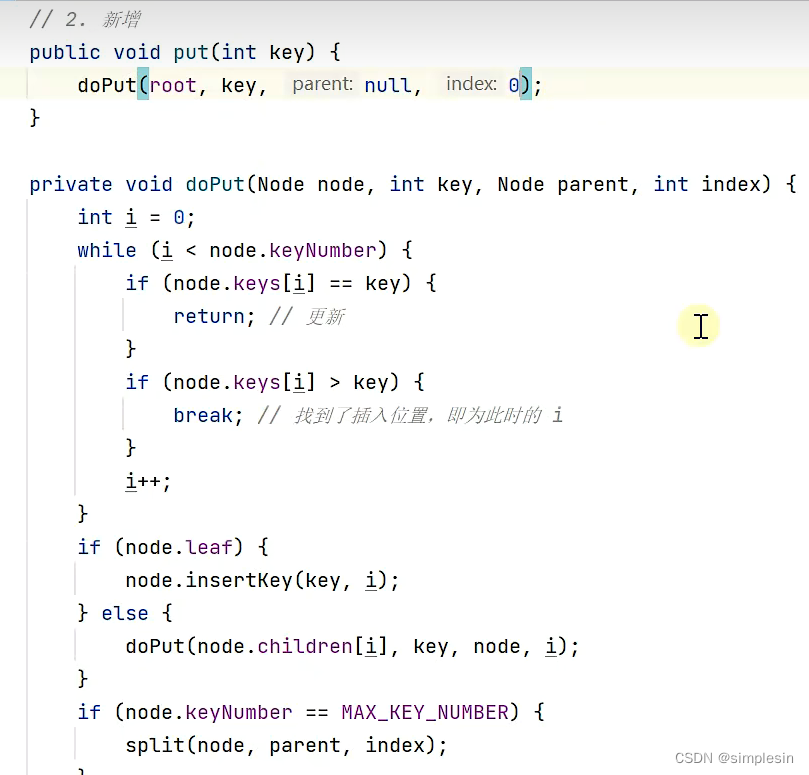
166? B树 put结合split
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!