机器学习-逻辑回归

一、引言

逻辑回归（Logistic Regression）是一种广泛应用于分类问题的监督学习算法。尽管名字中含有“回归”二字，但这并不意味着它用于解决回归问题。相反，逻辑回归专注于解决二元或多元分类问题，如邮件是垃圾邮件还是非垃圾邮件，一个交易是欺诈还是合法等。

逻辑回归源于统计学，旨在模拟一个因变量和一个或多个自变量之间的关系。与线性回归不同，逻辑回归并不直接预测数值，而是估计样本属于某一类别的概率。这通常通过Sigmoid函数（或对数几率函数）来实现，该函数能够将任何实数映射到0和1之间。

为了理解这种概率模型的重要性，我们可以考虑一下现代应用的复杂性。从金融风险评估、医疗诊断，到自然语言处理和图像识别，逻辑回归都找到了广泛的应用。它之所以受欢迎，一方面是因为其模型简单，易于理解和解释；另一方面是因为它在处理大量特征或者处理非线性关系时也具有很高的灵活性。

逻辑回归的算法实现通常基于最大似然估计（Maximum Likelihood Estimation, MLE），这是一种针对模型参数进行估计的优化算法。通过优化损失函数，算法试图找到最有可能解释观测数据的模型参数。

虽然逻辑回归在许多方面都很优秀，但它也有其局限性。例如，它假定因变量和自变量之间存在线性关系，这在某些复杂场景下可能不成立。然而，通过特征工程和正则化等手段，这些问题往往可以得到缓解。

总体而言，逻辑回归是机器学习领域中不可或缺的工具，其背后的数学原理和实际应用都值得深入研究。通过本文，我们将深入探讨逻辑回归的各个方面，以期提供一个全面、深入且易于理解的视角。

---

二、逻辑回归基础

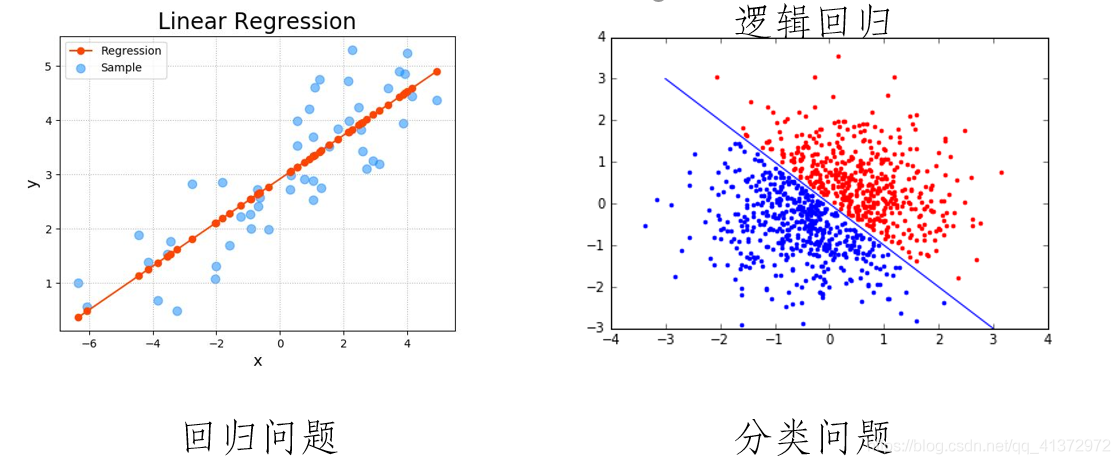
逻辑回归是一种针对分类问题的监督学习模型。它起源于统计学，尤其是当我们希望预测一个二元输出时，逻辑回归成为一个非常实用的工具。

从线性回归到逻辑回归

逻辑回归的思想是基于线性回归的，但有几个关键的不同点。在线性回归中，我们试图拟合一个线性方程来预测一个连续的输出值。然而，在逻辑回归中，我们不是直接预测输出值，而是预测输出值属于某一特定类别的概率。

举例：医学检测

假设我们有一个用于检测某种疾病（如糖尿病）的医学测试。在这种情况下，线性回归可能会预测一个人患疾病的程度或严重性。但逻辑回归更进一步：它会预测一个人患疾病的概率，并根据这个概率进行分类——例如，概率大于0.5则判断为阳性。

Sigmoid 函数

逻辑回归中最关键的组成部分是 Sigmoid（或称为 logistic）函数。这个函数接受任何实数作为输入，并将其映射到0和1之间，使其可以解释为概率。

举例：考试成绩与录取概率

考虑一个学生根据其考试成绩被大学录取的例子。线性回归可能会直接预测录取概率，但数值可能会超过[0,1]的范围。通过使用 Sigmoid 函数，我们可以确保预测值始终在合适的范围内。

损失函数

在逻辑回归中，最常用的损失函数是交叉熵损失（Cross-Entropy Loss）。该损失函数度量模型预测的概率分布与真实概率分布之间的差距。

举例：垃圾邮件分类

假设我们正在构建一个垃圾邮件过滤器。对于每封邮件，模型会预测这封邮件是垃圾邮件的概率。如果一封实际上是垃圾邮件（y=1）的邮件被预测为非垃圾邮件（yhat约等于0），损失函数的值会非常高，反之亦然。

优点与局限性

优点

1. 解释性强：逻辑回归模型易于理解和解释。
2. 计算效率：模型简单，训练和预测速度快。
3. 概率输出：提供预测类别的概率，增加了解释性。

局限性

1. 线性边界：逻辑回归假设数据是线性可分的，这在某些复杂场景下可能不成立。
2. 特征选择：逻辑回归对于不相关的特征和特征之间的相互作用比较敏感。

通过这个章节，我们可以看到逻辑回归在简洁性和解释性方面有着显著的优点，但同时也存在一定的局限性。

---

三、数学原理

理解逻辑回归背后的数学原理是掌握这一算法的关键。这部分将深入解析逻辑回归的数学结构，包括概率模型、损失函数优化和特征选择。

概率模型

举例：信用卡交易

想象你正在开发一个用于检测信用卡欺诈交易的模型。在这种情况下，(X) 可能包括交易金额、地点、时间等特征，模型会输出这笔交易是欺诈交易的概率。

损失函数与最大似然估计

最常用于逻辑回归的损失函数是交叉熵损失。这其实是最大似然估计（MLE）在逻辑回归中的具体应用。

举例：电子邮件分类

假设你正在构建一个电子邮件分类器来区分垃圾邮件和正常邮件。使用交叉熵损失函数，你可以通过最大化似然函数来“教”模型如何更准确地进行分类。

梯度下降优化

举例：股票价格预测

虽然逻辑回归通常不用于回归问题，但梯度下降的优化算法在很多其他类型的问题中也是通用的。例如，在预测股票价格时，同样可以使用梯度下降来优化模型参数。

特征选择与正则化

特征选择在逻辑回归中非常重要，因为不相关或冗余的特征可能会导致模型性能下降。正则化是一种用于防止过拟合的技术，常见的正则化方法包括 L1 正则化和 L2 正则化。

举例：房价预测

在房价预测模型中，可能有很多相关和不相关的特征，如面积、地段、周围学校数量等。通过使用正则化，你可以确保模型在拟合这些特征时不会过于复杂，从而提高模型的泛化能力。

通过本章的讨论，我们不仅深入了解了逻辑回归的数学基础，还通过具体的例子和应用场景，让这些看似复杂的数学概念更加贴近实际，易于理解。这有助于我们在实际应用中更加灵活地使用逻辑回归，以解决各种分类问题。

---

四、实战案例

实战是学习逻辑回归的最佳方式。在这一部分，我们将使用Python和PyTorch库来实现一个完整的逻辑回归模型。我们将使用经典的鸢尾花（Iris）数据集，该数据集包括四个特征：萼片长度、萼片宽度、花瓣长度、花瓣宽度，以及一个标签，用于区分三种不同类型的鸢尾花。

数据准备

首先，我们需要加载和准备数据。

# 导入所需库
import torch
import torch.nn as nn
import torch.optim as optim
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

# 加载数据
iris = load_iris()
X, y = iris.data, iris.target

# 由于逻辑回归是二分类模型，我们只取其中两类数据
X, y = X[y != 2], y[y != 2]

# 数据分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 转换为PyTorch张量
X_train = torch.FloatTensor(X_train)
X_test = torch.FloatTensor(X_test)
y_train = torch.LongTensor(y_train)
y_test = torch.LongTensor(y_test)

模型构建

接下来，我们定义逻辑回归模型。

class LogisticRegression(nn.Module):
    def __init__(self, input_dim):
        super(LogisticRegression, self).__init__()
        self.linear = nn.Linear(input_dim, 1)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        return self.sigmoid(self.linear(x))

模型训练

现在我们可以开始训练模型。

# 初始化模型、损失函数和优化器
model = LogisticRegression(X_train.shape[1])
criterion = nn.BCELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)

# 训练模型
for epoch in range(1000):
    model.train()
    optimizer.zero_grad()

    # 前向传播
    outputs = model(X_train).squeeze()
    loss = criterion(outputs, y_train.float())

    # 反向传播和优化
    loss.backward()
    optimizer.step()

    if (epoch + 1) % 100 == 0:
        print(f'Epoch [{epoch+1}/1000], Loss: {loss.item()}')

模型评估

最后，我们用测试集来评估模型的性能。

# 测试模型
model.eval()
with torch.no_grad():
    test_outputs = model(X_test).squeeze()
    test_outputs = (test_outputs > 0.5).long()
    accuracy = (test_outputs == y_test).float().mean()
    print(f'Accuracy: {accuracy.item()}')