二叉堆的简单板子+理解+例题
首先,我们先要了解堆是什么?
堆:是一种高级树状数据结构,是一种完全二叉树。
(完全二叉树指的是,除了叶子节点,每个节点均有左右两个子节点的树状结构)
而,二叉堆是堆的最常见的实现方式。
二叉堆又可以分为:大根堆,小根堆。(可以用c++ 的 stl实现)
大根堆:每一个节点,大于等于其子节点。(从堆顶到堆底不严格递增)小根堆:每一个节点,小于等于其子节点。(从堆顶到堆底不严格递减)
那么对于二叉堆,我们是需要手动去实现一些它的一些基本操作。
- 向下调整
- 向上调整
- 插入一个元素
- 求堆中最大值/最小值(堆顶)
- 删除堆中最大值/最小值
下面先实现最大堆/大根堆的操作:
1.使用vector容器实现:
//定义一个最大堆,先给里面装填一个空元素,使得后续插入的元素下标一一对应:
//意思是,第一个数的下标就是 1,而不是0 ,同时也是 size() -1
vector<int > big(1);2.向上调整
void upp(int pos) {
while (pos > 1) { // 循环直到节点到达堆顶
if (big[pos] > big[father]) { // 如果当前节点的值大于其父节点的值
swap(big[pos], big[father]); // 交换当前节点与父节点的值
}
else break; // 如果不满足最大堆性质,终止循环
pos = father; // 更新当前节点的位置为父节点
}
}
3.向下调整
void down(int pos) {
int size = big.size(); // 获取堆的大小
while (2*pos <= size-1) { // 当前节点有至少一个子节点时循环
int son;
if (rson <= size - 1 and big[lson] < big[rson]) { // 如果当前节点有右子节点且右子节点的值大于左子节点的值
son = rson; // 则选取右子节点作为子节点
}
else son = lson; // 否则选取左子节点作为子节点
if (big[pos] < big[son])swap(big[son], big[pos]); // 如果当前节点的值小于子节点的值,则交换它们的位置
else break; // 如果不满足最大堆性质,终止循环
pos = son; // 更新当前节点的位置为子节点
}
}
4.插入一个数:
void insert(int val) {
big.push_back(val); // 将元素 val 添加到堆的末尾
upp(big.size() - 1); // 调用 upp 函数,以维护最大堆性质
}
5.删除最大值:
void earse_big() {
if (big.size() > 1) { // 如果堆中有至少两个元素
big[1] = big[big.size() - 1]; // 将第一个元素用最后一个元素覆盖
big.pop_back(); // 删除最后一个元素
down(1); // 对堆顶元素进行向下调整,以满足最大堆性质
}
}6.返回最大值:
int get_max() {
if (big.size() > 1) {
return big[1];
}
}
以上就是二叉堆中的最大堆实现的过程。
不过在实际的写题中,我们不需要每次手写一个二叉堆。
可以直接用现成的stl 容器,priority_queue;
下面简单介绍以下stl的用法:
priority_queue<int> bigheap; //priority_queue 默认大根堆
priority_queue<int, vector<int>, greater<int> > littleheap; // 如果要定义小根堆,就要写全参数
// priority_queue 的参数为: 数据类型、容器类型、定义类型。
//如果是小根堆, 我们在第三个参数那里改成: greater<int>
//如果是大根堆:完整的写法就是: priority_queue<int , vector<int> , less<int> > 堆的名字
然后,下面是一些堆的函数:
priority_queue<int> big;
priority_queue<int, vector<int>, greater<int> > little;
int main() {
big.push(1); //插入的同时自动调整位置
big.pop();//删除堆顶元素
big.top()//返回堆顶元素 最大值/最小值
}下面给一道堆的模板题:
P3378 【模板】堆 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)![]() https://www.luogu.com.cn/problem/P3378答案:
https://www.luogu.com.cn/problem/P3378答案:
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<cstdio>
#include<cmath>
#include<string>
#include<cstring>
#include<algorithm>
#include<vector>
#include<cctype>
#include<map>
#include<set>
#include<queue>
#include<numeric>
#include<iomanip>
#include<stack>
#include<list>
using namespace std;
#define ll long long
#define lson pos<<1
#define rson (pos<<1)|1
#define father pos>>1
const int N = 1e6 + 7;
//二叉堆:
// 最大堆,最小堆
// 最大堆要满足一个性质:任意一个节点,如果它的子节点存在的话,这个节点的值是要大于等于它的子节点的任意的值
//
// 1、向下调整的函数
// 2、向上调整的函数
// 3、向一堆数据中插入一个元素
// 4、在一堆数据中删除一个元素(最大值)
// 5、求出一堆数据里面的最大值。
//
//
vector<int > heap(1);
void heapup(int pos) { //node 指的是vector下标
while (pos > 1) {
if (heap[pos] < heap[father]) {
swap(heap[pos], heap[father]);
}
else {
break;
}
pos = father;
}
}
//第一个问题: 为什么heapdown函数中 循环的条件要取等
void heapdown(int pos) {
int size = heap.size(); //实际上堆里面的元素为 size-1, size指的是一个空的下标
while ( lson < size) {
int son;
if (rson<size and heap[lson] > heap[rson]) {
son = rson;
}
else son = lson;
if (heap[pos] < heap[son])break;
else {
swap(heap[pos], heap[son]);
}
pos = son;
}
}
void insert(int val) {
heap.push_back(val);
int size = heap.size();
heapup(size - 1);
}
int get_min() {
return heap[1];
}
void earse_min() {
if (heap.size() > 1) {
heap[1] = heap[heap.size() - 1];
heap.pop_back();
heapdown(1);
}
}
bool empty() {
if (heap.size() > 1)return true;
else return false;
}
int main() {
int n;
cin >> n;
while (n--) {
int op;
cin >> op;
if (op == 1) {
int x;
cin >> x;
insert(x);
}
else if (op == 2) {
cout<<get_min();
cout << '\n';
}
else {
earse_min();
}
}
}下面讲一下,二叉堆的综合运用:
1. 对顶堆
先给一个模板题,来看看对顶堆的使用场景
P1801 黑匣子 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)![]() https://www.luogu.com.cn/problem/P1801然后,来介绍一下对顶堆:
https://www.luogu.com.cn/problem/P1801然后,来介绍一下对顶堆:
堆顶堆由两个堆组成,一个大根堆,一个小根堆。
比如一遍往堆里插入元素,一遍问第i大的元素是哪个?
我们可以这样写:
它问第i大的元素是哪个?
我们就可以构造出一个这样的形状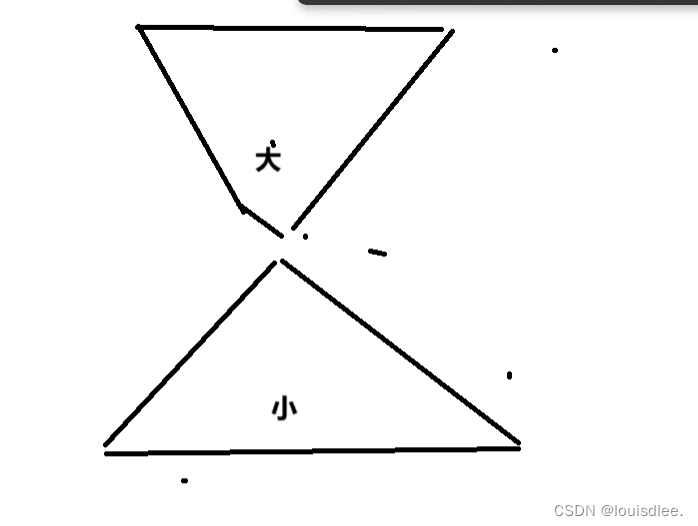
?不断往小根堆中插入元素,直到插满i个元素,此后的话,执行这样一个操作:
先往小根堆里插入元素,然后取出小根堆的堆顶,加入上面的大根堆,然后删除小根堆的堆顶。
这样就实现了一个目的:
小根堆内的元素仍然是i个,但在新元素插入后,调整了大小关系,仍然使得小根堆的堆顶的元素是当前的第i大的元素(即时现在有超过i个元素,大于第i大的元素,都被放到了大根堆里)
如果i开始变化,如i变成i+1,那么我们直接把当前大根堆的堆顶的元素加入小根堆中,这个元素一定会在小根堆的堆顶,然后我们在删除大根堆的堆顶,使之调整结构
那么对于求第i小的元素,我们也是同样的道理,只要下面放大根堆,上面放小根堆,维护大根堆内的元素为i个,那么大根堆的堆顶就是在当前两个堆中,第i小的那个元素:
上题解:
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<cstdio>
#include<cmath>
#include<string>
#include<cstring>
#include<algorithm>
#include<vector>
#include<cctype>
#include<map>
#include<set>
#include<queue>
#include<numeric>
#include<iomanip>
#include<stack>
#include<list>
using namespace std;
#define ll long long
#define lson pos<<1
#define rson (pos<<1)|1
#define father pos>>1
const int N = 2e6 + 7;
priority_queue<int> bigheap;
priority_queue<int, vector<int>, greater<int> > littleheap;
int a[N];//元素
int opt[N];//操作
int main() {
int m, n; //元素个数,操作个数
cin >> m >> n;
for (int i = 1; i <= m; i++) {
cin >> a[i];
}
for (int j = 1; j <= n; j++) {
cin >> opt[j];
}
int tot = 1, j = 1;
for (int i = 1; i <= m; i++) {
bigheap.push(a[i]);
if (bigheap.size() >= tot) {
littleheap.push(bigheap.top());
bigheap.pop();
}
while (i == opt[j]) {
cout << littleheap.top() << endl;
bigheap.push(littleheap.top());
littleheap.pop();
j++;
tot++;
}
}
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!