MATLAB - 凸优化（Convex Optimization）

2023-12-13 11:53:10

系列文章目录

前言

????????凸优化（Convex optimization）是在凸约束（convex constraints）条件下使凸目标函数（convex objective function）最小化的过程，或者等同于在凸约束条件下使凹目标函数最大化的过程。对于许多凸优化问题，满足局部最优（local optimality）条件的点都能被有效地找到。由于局部最优点也是全局最优（global optimum）点，因此只需找到局部最优点即可解决问题。非凸问题的凸近似提供了最优目标值（optimal objective value）和近似解（approximate solutions）的边界。

????????下图展示了凸优化和非凸优化问题的示例。

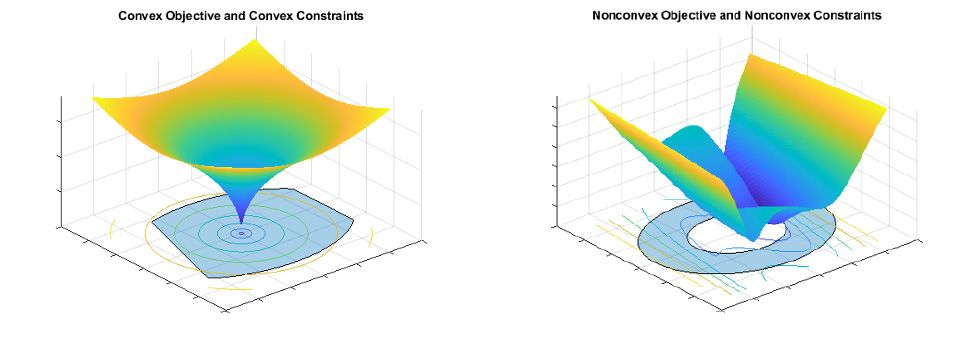
????????凸优化的应用遍及金融和工程领域，包括投资组合优化（portfolio optimization）、设计优化（design optimization）、参数估计（parameter estimation）、信号处理（signal processing）和最优控制（optimal control）。例如，选择一个股票投资组合，使其收益最大化，但风险和跟踪误差不得超过基准投资组合的上限，这个问题可以表述为一个凸优化问题。

????????凸优化是一个数学问题，即找到一个向量 x? 的数学问题：

$m i n_{x}f(x)$

满足条件

$g_{i}(x)\leq0$????????（nonlinear inequality constraints - 非线性不等式约束）

$A x\leq b$????????（linear inequality constraints - 线性不等式约束）

$A_{e q}x=b_{e q}$? ? ? ? （linear equality constraints - 线性等式约束）

$l b\leq x\leq u b$? ? ? ? （bound constraints - 范围约束条件）

其中，$g_{i},i=1,\cdot\cdot,m$ ?都是凸函数。

线性规划（Linear programs，LP）和凸二次规划（convex?quadratic programs，QP）是凸优化问题（convex optimization problems）。不等式约束为凸锥的圆锥优化（Conic optimization）问题也属于凸优化问题。具有线性或凸二次方目标以及线性和凸二次方约束的问题（convex quadratic constraints，QCQP）可以表示为二阶锥形规划（second-order cone programs，SOCP），从而可以用高效的凸优化方法求解。

内点法（Interior point algorithms）通常用于解决凸优化问题，可使用矩阵运算和 Cholesky 因式分解（Cholesky factorization）或块 LDL' 因式分解（block LDL’ factorization）在 MATLAB? 中编写。Optimization Toolbox?（Optimization Toolbox?） 拥有线性规划（linear programs）、二次规划（quadratic programs）、非线性规划（nonlinear programs）和二阶锥形规划（second-order cone programs）的内点法实现，适用于大规模问题。

有关解决凸优化问题的更多信息，请参阅优化工具箱（Optimization Toolbox）。

一、线性规划（Linear Programming）

????????线性规划（Linear programming），又称线性优化（linear optimization），是指在约束条件（bounds）、线性等式（linear equality）和线性不等式约束下，使线性目标函数（linear objective function）最小化或最大化。实例问题包括加工业中的混合（blending）、制造业中的生产规划（production planning）、金融业中的现金流匹配（cash flow matching）以及能源和运输业（energy and transportation）中的规划。

线性规划是一个数学问题，即找到一个向量 x 的数学问题：

$\operatorname*{min}_{x}\left\{f^{\mathsf{T}}x\right\}$

满足约束

$A x\leq b$

$A_{e q}x=b_{e q}$

$l b\leq x\leq u b$

1.1?用 MATLAB 进行线性规划

????????您可以使用 MATLAB? 实现以下常用算法来解决线性规划问题：

  • 内部点（Interior point）： 使用初等 - 二元预测 - 校正（primal-dual predictor-corrector）算法，尤其适用于具有结构或可使用稀疏矩阵定义的大规模线性规划。
  • 单纯形（Simplex）：使用系统程序生成和测试线性程序的候选顶点解。单纯形算法和相关的对偶-单纯形算法是线性优化中使用最广泛的算法。

????????优化工具箱?中的 linprog（linprog） 求解器实现了这些线性优化技术。

二、二次规划 - Quadratic Programming

二次规划（QP）是指在边界、线性相等和不相等约束条件下，使目标函数最小化或最大化。这类问题的例子包括金融领域的投资组合优化（portfolio optimization）、电力公司的发电优化和工程领域的设计优化（design optimization）。

二次规划是一个数学问题，即找到一个能使二次函数最小化的向量 x：

$\operatorname*{min}_{x}\left\{?{\frac{1}{2}}x^{\mathsf{T}}H x+f^{\mathsf{T}}x\right\}$

满足条件：

$A x\leq b$

$A_{e q}x=b_{e q}$

$l b\leq x\leq u b$

您可以使用 MATLAB? 实现以下常用算法来解决二次编程问题：

有关二次规划的更多信息，请参阅优化工具箱?。

文章来源:https://blog.csdn.net/weixin_46300916/article/details/134867220
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。