基于 Stereo R-CNN 的自动驾驶 3D 目标检测

论文地址：https://openaccess.thecvf.com/content_CVPR_2019/papers/Li_Stereo_R-CNN_Based_3D_Object_Detection_for_Autonomous_Driving_CVPR_2019_paper.pdf
论文代码：https://github.com/HKUST-Aerial-Robotics/Stereo-RCNN

论文背景

大多数 3D 物体检测方法严重依赖 LiDAR 数据来在自动驾驶场景中提供准确的深度信息。然而，LiDAR 的缺点是成本高、感知范围相对较短（～100 m）和信息稀疏（与 >720p 图像相比为 32、64 线）。另一方面，单目相机为 3D 物体检测提供了替代的低成本解决方案。
深度信息可以通过场景中的语义属性和物体大小等来预测。然而，推断的深度不能保证准确性，特别是对于未见过的场景。

基于单目的方法不可避免地会缺乏准确的深度信息，与单目相机相比，立体相机通过左右 photometrix 对准提供更精确的深度信息。与激光雷达相比，立体相机成本较低，同时对于具有重要视差的物体也能实现相当的深度精度。立体相机的感知范围取决于焦距和基线。因此，立体视觉具有通过组合不同焦距和基线的不同立体模块来提供更大范围感知的潜在能力。

论文框架

在这篇论文中，通过充分利用立体图像中的语义和几何信息来研究 3D 对象的稀疏和稠密约束，并提出一种基于立体 R-CNN 的精确 3D 目标检测方法。Stereo R-CNN 同时检测和关联左右图像的目标。

网络架构如图 1 所示，可分为三个主要部分。
Stereo RPN 模块，它输出相应的左右 RoI proposal。
分别在左右特征图上应用 RoI Align 后，连接左右 RoI 特征来对对象类别进行分类，并在 stereo regression 分支中回归准确的 2D 立体框、视点和尺寸。关键点分支用于仅使用左 RoI 特征来预测目标关键点。
这些输出形成了 3D 框估计的稀疏约束（2D 框、关键点），其中制定了 3D 框 corners与 2D 左右框和关键点之间的投影关系。

为确保3D 定位性能的关键组件是密集的 3D 框对齐。论文将 3D 目标定位视为学习辅助几何问题，而不是端到端回归问题。没有直接使用没有明确利用对象属性的深度输入，而是将对象 RoI 视为一个整体而不是独立的像素。对于规则形状的物体，可以根据粗略的 3D 边界框推断出每个像素与 3D 中心之间的深度关系。

论文根据与 3D 目标中心的深度关系将左侧 RoI 中的密集像素扭曲到右侧图像，以找到最小化整个光度误差的最佳中心深度。整个目标 RoI 从而形成 3D 对象深度估计的密集约束。根据对齐的深度和 2D 测量结果，使用 3D 框估计器进一步校正 3D 框。

论文内容

与 Faster R-CNN 等单帧检测器相比，Stereo R-CNN 只需稍作修改就可以同时检测和关联左右图像的 2D 边界框。论文使用权重共享 ResNet-101 和 FPN 作为主干网络来提取左右图像上的一致特征。

Stereo RPN

区域提议网络（RPN）是一种基于滑动窗口的前景检测器。特征提取后，利用 3×3 卷积层来减少通道，然后使用两个同级全连接层对每个输入位置的对象性和回归框偏移进行分类，该输入位置使用预定义的多尺度框进行锚定。
与 FPN 类似，论文通过评估多尺度特征图上的锚来修改金字塔特征的原始 RPN。不同之处在于论文在每个尺度连接左右特征图，然后将连接的特征输入立体 RPN 网络。

能够同时进行目标检测和关联的关键设计是目标分类器和立体框回归器的不同真实值（GT）框分配。

论文将左右 GT 框的并集（称为并集GT框）指定为对象性分类的目标。如果锚点与任一并集 GT 框的交集比 (IoU) 高于 0.7，则为该锚点分配正标签；如果其与任一并集框的 IoU 低于 0.3，则为该锚点分配负标签。因此，正锚点往往包含左侧和右侧对象区域。

计算正锚点相对于目标联合 GT 框中包含的左右 GT 框的偏移量，然后分别将偏移量分配给左回归和右回归。立体回归量有六个回归项：$[\Delta u,\Delta w,\Delta u^{{}^{\prime }},\Delta w^{{}^{\prime }},\Delta v,\Delta h]$，其中 $u,v$ 表示图像空间中 2D 框中心的水平和垂直坐标，$w,h$ 表示框的宽度和高度，上标 $(?{)}^{{}^{\prime }}$表示右图中的对应项。对左框和右框使用相同的 $\Delta v,\Delta h$ 偏移量，因为要使用校正过的图像。因此，有六个用于 stereo RPN 回归器的输出通道，而不是原始 RPN 实现中的四个输出通道。由于左右 proposal 是从同一个 anchor 生成的并且共享 objectness 分数，因此它们可以自然地一一关联。分别对左右 RoI 使用非极大值抑制 (NMS) 来减少冗余，然后从保留在左右 NMS 中的条目中选择前 2000 个候选者进行训练。为了进行测试，仅选择前 300 名候选者。

Stereo R-CNN

Stereo 回归

在 Stereo RPN 之后，得到相应的左右提案对。在适当的金字塔级别分别在左侧和右侧特征图上应用 RoI Align [1]。左右 RoI 特征被连接并输入两个连续的全连接层（每个层后面都有一个 ReLU 层）以提取语义信息。使用四个子分支分别预测对象类、立体边界框、尺寸和视点角度。

[1] K. He, G. Gkioxari, P. Doll′ar, and R. Girshick. Mask r-cnn. In Computer Vision (ICCV), 2017 IEEE International Conference on, pages 2980–2988. IEEE, 2017.

视点角度不等于从裁剪图像 RoI 中无法观察到的物体方向。

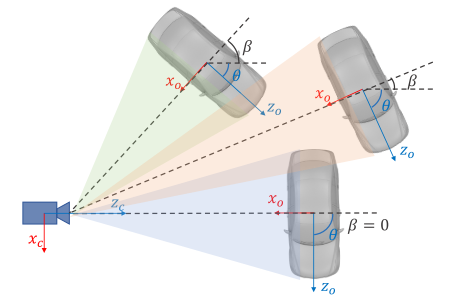
论文使用 $\theta$ 表示相对于相机框架的车辆方向，使用 $\beta$ 表示相对于相机中心的物体方位角。三辆车的方向不同，但是它们在裁剪后的 RoI 图像上的投影完全相同。因此，将视点角度 $\alpha$ 回归定义为：$\alpha =\theta +\beta$。为了避免不连续性，训练目标是 $[\sin \alpha ,\cos \alpha ]$ 对而不是原始角度值。

借助立体框和物体尺寸，可以直观地恢复深度信息，并且还可以通过解耦视点角度与3D位置之间的关系来解决车辆方向。
在对 RoI 进行采样时，如果左侧 RoI 与左侧 GT 框之间的最大 IoU 高于 0.5，同时右侧 RoI 与相应右侧 GT 框之间的 IoU 也高于 0.5，则我们将左右 RoI 对视为前景。如果左 RoI 或右 RoI 的最大 IoU 位于 $[0.1,0.5)$ 区间内，则左右 RoI 对被视为背景。对于前景 RoI 对，通过计算左侧 RoI 与左侧 GT 框之间的偏移量以及右侧 RoI 与相应右侧 GT 框之间的偏移量来分配回归目标。仍然对左右 RoI 使用相同的 $\Delta v,\Delta h$。对于维度预测，只需将真实维度与先验维度之间的偏移量回归即可。

关键的预测

除了立体框和视点角度之外，论文注意到投影在框中间的3D框 corners 可以为3D盒估计提供更严格的约束。

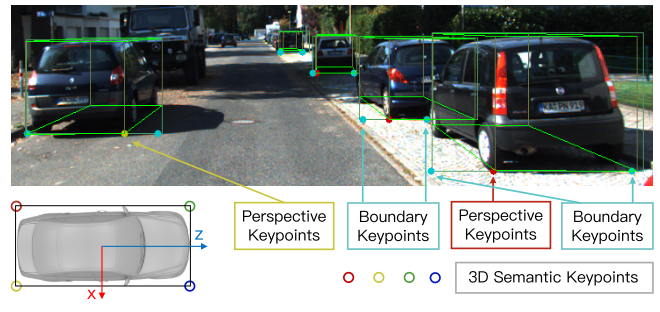
定义了四个 3D 语义关键点，表示 3D 边界框底部的四个角。只有一个 3D 语义关键点可以明显投影到框中间（而不是左边缘或右边缘）。将这个语义关键点的投影定义为透视关键点。
论文还预测了两个边界关键点，它们可以作为规则形状对象的实例掩模的简单替代方案。只有两个边界关键点之间的区域属于当前对象，并将用于进一步的密集对齐。
论文按照 Mask R-CNN 中的 proposal 预测关键点。仅左侧特征图用于关键点预测。将 $14\times 14$ RoI 对齐的特征图输入到六个连续的 256-d $3\times 3$ 卷积层，每个卷积层后面都有一个 ReLU 层。使用 $2\times 2$ 反卷积层将输出尺度上采样至 $28\times 28$。可以发现，除了 2D 框之外，只有关键点的 $u$ 坐标提供了附加信息。
为了简化任务，论文对 $6\times 28\times 28$ 输出中的高度通道求和以产生 $6\times 28$ 预测。因此，RoI 特征中的每一列都将被聚合并有助于关键点预测。前四个通道表示四个语义关键点中的每一个被投影到相应的 $u$ 位置的概率。另外两个通道分别表示每个 $u$ 位于左边界和右边界的概率。要注意的是，四个 3D 关键点中只有一个可以明显投影到 2D 框中间，因此将 softmax 应用于 $4\times 28$ 输出，从而将一个专有语义关键点投影到单个位置。该策略避免了透视关键点类型（对应于哪个语义关键点）可能出现的混淆。对于左右边界关键点，分别对 $1\times 28$ 输出应用 softmax。

在训练过程中，最小化 $4\times 28$ softmax 输出的交叉熵损失以进行透视关键点预测。 $4\times 28$ 输出中只有一个位置被标记为透视关键点目标。忽略了没有 3D 语义关键点明显投影在框中间的情况（例如，截断和正交投影情况）。对于边界关键点，独立地最小化两个 $1\times 28$ softmax 输出的交叉熵损失。每个前景RoI将根据GT框之间的遮挡关系分配左右边界关键点。

3D Box 估计

利用稀疏关键点和 2D 框信息来求解粗略 3D 边界框。
3D 边界框的状态可以用 x = { x , y , z , θ } x = \{x, y, z, θ\} x={x,y,z,θ} 表示，分别表示 3D 中心位置和水平方向。
给定左右 2D 框、透视关键点和回归维度，可以通过最小化 2D 框和关键点的重投影误差来求解 3D 框。

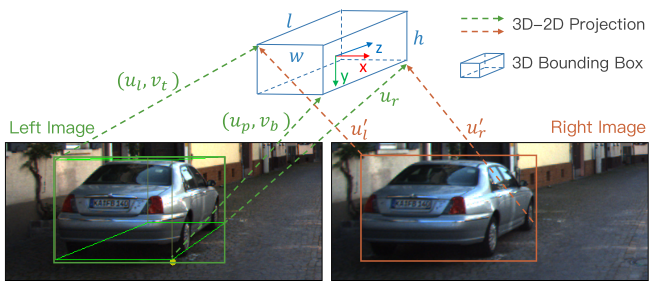
从 stereo 框和透视关键点中提取七个测量值： z = { u l , v t , u r , v b , u l ′ , u r ′ , u p } z =\{u_l, v_t, u_r, v_b, u_l^{'}, u_r^{'}, u_p\} z={ul?,vt?,ur?,vb?,ul′?,ur′?,up?}，它们代表左 2D 框的左、上、右、下边缘，左，右侧 2D 框的右边缘，以及透视关键点的 $u$ 坐标。每个测量值均由相机内部标准化，以简化表示。给定透视关键点，可以推断出 3D 框 corners 和 2D 框边缘之间的对应关系。
通过投影变换制定3D-2D关系：
$$\begin{gathered} v_t=(y?\frac{h}{2})/(z?\frac{w}{2}\sin \theta ?\frac{l}{2}\cos \theta ), \\ {u}_l=(x?\frac{w}{2}\cos \theta ?\frac{l}{2}\sin \theta )/(z+\frac{w}{2}\sin \theta ?\frac{l}{2}\cos \theta ), \\ {u}_p=(x+\frac{w}{2}\cos \theta ?\frac{l}{2}\sin \theta )/(z?\frac{w}{2}\sin \theta ?\frac{l}{2}\cos \theta ), \\ ... \\ {u}_r^{{}^{\prime }}=(x?b+\frac{w}{2}\cos \theta +\frac{l}{2}\sin \theta )/(z?\frac{w}{2}\sin \theta +\frac{l}{2}\cos \theta ) \end{gathered}$$

使用 $b$ 表示立体相机的基线长度，使用 $w$、$h$、$l$ 表示回归尺寸。共有七个方程对应七个测量值，其中 { w 2 , l 2 } \{\frac {w}{2},\frac {l}{2}\} {2w?,2l?} 的符号应根据对应的3D框子角点适当改变。上述七个方程的截边被删除。这些多元方程通过高斯-牛顿法求解。通过联合利用 stereo 框和回归维度来更鲁棒地恢复 3D 深度信息。

在某些情况下，可以完全观察到少于两个侧面并且没有向上的透视关键点（例如，截断、正交投影），从纯几何约束中无法观察到方向和尺寸。使用视点角α来补偿不可观测的状态：$$\alpha =\theta +\arctan (?\frac{x}{z})$$ 通过 2D 框和透视关键点求解，粗糙的 3D 框具有精确的投影并且与图像很好地对齐，使得能够进一步密集对齐。

密集 3D 框对齐

左右边界框提供了 object-level 视差信息，以便我们可以粗略地求解 3D 边界框。然而，立体框是通过聚合 $7\times 7$ RoI 特征图中的高级信息来回归的。由于多个卷积滤波器，原始图像中包含的像素级信息（例如角点、边缘）会丢失。
为了实现亚像素匹配精度，论文检索原始图像以利用像素级高分辨率信息。要注意的是，论文的任务与像素级视差估计问题不同，其中结果可能会在不适定区域遇到不连续性（SGM），或在边缘区域出现过度平滑（基于 CNN 的方法）。论文仅在使用 dense object patch 时解决 3D 边界框中心的视差，即使用大量像素测量来解决单个变量。
将目标视为规则形状的立方体，可以知道每个像素与3D 边界框中心之间的深度关系。 为了排除属于背景或其他目标的像素，论文定义了一个有效的 RoI，该区域位于左右边界关键点之间，并且位于 3D 框的下半部，因为车辆的下半部适合 3D 框更紧密。
对于位于左图像有效 RoI 中归一化坐标 $(u_i,v_i)$ 的像素，光度误差可定义为：$$e_i=||I_l(u_i,v_i)?I_r(u_i?\frac{b}{z+\Delta z_i},v_i)||$$
其中，用 $I_l,I_r$ 分别表示左右图像的 3 通道 RGB 向量；$\Delta z_i=z_i?z$ 像素 $i$ 与 3D 框中心的深度差； $b$ 基线长度。$z$ 是需要解决的唯一目标变量。
使用双线性插值来获得右侧图像上的子像素值。总匹配成本定义为有效 RoI 中所有像素的平方差之和 (SSD)：$$E=\sum _{i=0}^N{e}_i$$

中心深度 $z$ 可以通过最小化总匹配成本 $E$ 来求解，可以有效地枚举深度以找到最小化成本的深度。
首先在初始值周围以 0.5 米的间隔枚举 50 个深度值，以获得粗略的深度，最后在粗略深度周围以 0.05 米的间隔枚举 20 个深度值，以获得精确对齐的深度。然后，使用 3D 框估计器通过固定对齐深度来校正整个 3D 框。将目标 RoI 视为几何约束整体，论文的密集对齐方法自然避免了立体深度估计中的不连续性和不适定问题，并且对强度变化和亮度主导具有鲁棒性，因为有效 RoI 中的每个像素都会对对象做出贡献深度估计。
该方法非常高效，并且可以作为任何基于图像的 3D 检测的轻量级插件模块，以实现深度校正。尽管 3D 目标并不严格拟合 3D 立方体，但由形状变化引起的相对深度误差比全局深度小得多。

论文总结

论文提出了一种自动驾驶场景中基于 Stereo R-CNN 的 3D 目标检测方法。将 3D 目标定位表述为学习辅助几何问题，利用了目标的语义属性和密集约束。
论文提出的 3D 目标检测框架灵活实用，每个模块都可以扩展和进一步改进。例如，Stereo R-CNN 可以扩展用于多个对象检测和跟踪。可以用实例分割替换边界关键点，以提供更精确的有效 RoI 选择。通过学习物体形状，论文提出的3D 检测方法可以进一步应用于一般目标。