python解决动态规划算法问题，爬楼梯问题

2023-12-30 17:26:49

对于动态规划算法的经典问题中，找到爬到楼梯顶层的方法有多少种事一个比较基础也是比较经典的一个一维动态规划问题。问题的主要描述为，假如要爬一个n层的楼梯，每次只能走一个或者两个楼梯，总共有多少种方法可以爬到楼梯顶部。

如果说给定的楼顶层数n是2，那则有两种方式可以爬到楼顶，1+1或者是2阶这两种方式；如果说给定楼顶层数n是3，那则有1+1+1、1+2和2+1三种方式可以爬到楼顶。

添加图片注释，不超过 140 字（可选）

而对于整个问题的解析，可以分析一下，如果说想要爬到n层楼顶，有两种方式，一种是从n-1层向上爬一层就可以到楼顶，另外一种就是从n-2层向上爬2层到达楼顶，对于以上两种方式，分别只需要计算爬n-1层的爬楼方法数量和n-2的爬楼方法数量即可，然后将这两种方法数量相加其实就可以得到最终的爬楼方法数量。

而这也就可以说明，如果在计算爬到n层的方法，需要求出n-1层和n-2层的方法数量，而在计算n-1层方法数量是，又需要求出n-2层和n-3层方法数量，这也就产生了大量的重复计算，我们也就可以通过动态规划算法从底部数开始往上计算爬1,2，3,4，5,6...n的方法数量，并将每个方法数量存在一维数组，这也即是一维的动态规划算法问题。这里演示n=4时候的爬楼方式：

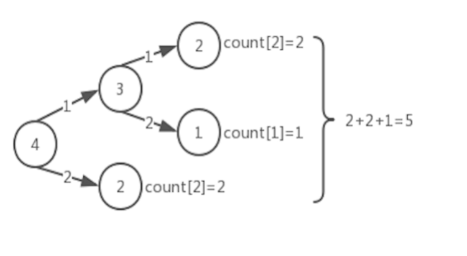
添加图片注释，不超过 140 字（可选）

总共有5种爬楼方式。

而整个完整的python代码实现如下：

def climbStairs(n):
    count = [0,1,2]
    for i in range(3,n+1):#填充一维数组过程
        count.append(count[i-1]+count[i-2])
    return count[n]

climbStairs(4)

文章来源:https://blog.csdn.net/Mrsawyer/article/details/135306550
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。