应用回归分析(7):岭回归、SST

2023-12-27 16:56:32

证明总偏差平方和 = 回归平方和 + 残差平方和_总偏差平方和残差平方和回归平方和-CSDN博客

7.1 简介

岭回归思想：使得 $MSE(\widehat{\beta }(k))$ 的值最小！！

岭回归式为了解决多重共线性问题

想法：当自变量存在多重共线性时， $|X'X|\approx 0$ 时，设想 $|X'X|$ 加上一个正常数矩阵 $kI$ ， $k>0$ ,那么 $X'X+kI$ 接近奇异值的程度就会变小。

注意 $y$ 可以标准化，也可以不标准化。如果 $y$ 也标准化，则 $\widehat{\beta}(k)$ 是标准化岭回归估计。

7.2 岭回归的性质

先知：均方误差：

注意均方误差中只有 $\widehat{\theta }$ 是随机变量哦！！！， $\theta$ 相当于常数。

证明1：

证明2：记住就行没有证明

证明3：回归分析|笔记整理（A）——岭回归，主成分回归（上） - 知乎 (zhihu.com)

参考这个【在最后】，但是我没看懂呜呜呜呜呜?

证明4：也参考上面那个（也没看懂啊啊啊啊啊）

总之就是记住：是无偏估计，但不是线性变换，二范数和均方误差都变小了

7.3 岭迹分析

7.3.1 不同情况的岭迹分析?

?1、 $\widehat{\beta _j}(0)=\widehat{\beta _j}>0$ ,且取值较大，从古典回归分析的观点看， $x_j$ 对 $y$ 有重要影响，且为正向影响

2、 $\widehat{\beta _j}(k)$ 不稳定，当k从0开始增加时， $\widehat{\beta _j}(k)$ 显著下降且迅速趋于零，从岭回归的观点看， $x_j$ 对 $y$ 不起重要作用，甚至可以剔除。

3、 $\widehat{\beta _j}(0)=\widehat{\beta _j}>0$ ，但很接近于0，从古典回归分析的观点看， $x_j$ 对 $y$ 影响不大

4、 $\widehat{\beta _j}(k)$ 不稳定，当k从0开始增加时， $\widehat{\beta _j}(k)$ 显著下降变为负值，从岭回归的观点看， $x_j$ 对 $y$ 有显著影响。

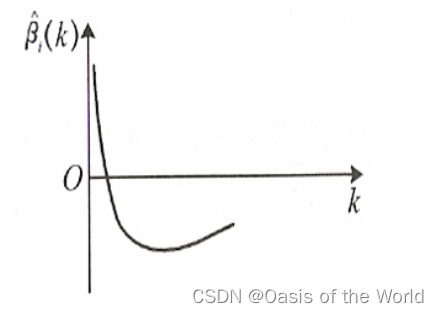
5、随着k的增加， $\widehat{\beta _j}(k)$ 迅速下降且稳定为负值，从岭回归的角度， $x_j$ 对 $y$ 有重要影响，且为负向影响

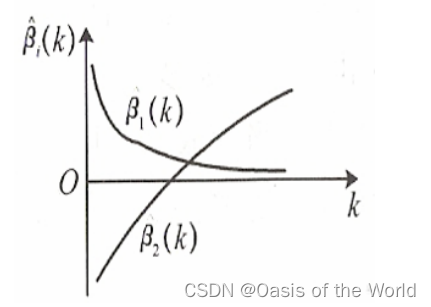
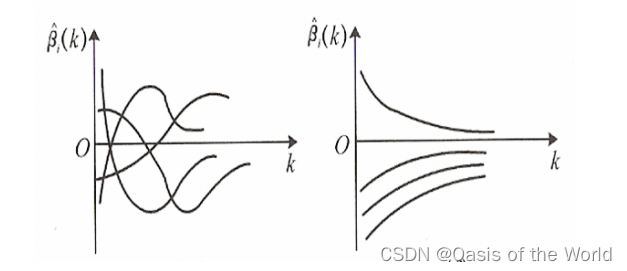
左边乱，怀疑最小二乘法。右边整齐，相信最小二乘法。

介于两者之间就要选择合适的K值

7.4 岭回归参数k的选择

7.4.1 通过岭迹图得到

见7.3 当所有的岭迹都趋于平稳时，就可以确定对应的值为k值

7.4.2 通过方差扩大因子

7.4.2 由残差平方和确定k值

岭估计 $\widehat{\beta }(k)$ 在减小均方误差的同时增大了残差平方和，希望将岭回归的残差平方和 $SSE(k)$ 的增加幅度控制在一定的限度以内，从而可以给一个大于1的c值，要求

$SSE(k)<cSSE$ ,寻找满足上述要求的最大的K值。

反正均方误差会变小是前面性质说的，岭回归为什么会使SSE变大哇？（以下是解释）

岭回归（Ridge Regression）是一种线性回归的改进方法，它通过在成本函数中引入正则化项，以解决普通线性回归中可能存在的多重共线性问题。在岭回归中，成本函数由两部分组成：回归平方和（SSR，Sum of Squared Errors）和正则化项。

成本函数（损失函数）表示为：

$J(\theta) = \text{SSR} + \lambda \sum_{i=1}^{n} \theta_i^2$

在岭回归中，通过引入正则化项，我们的目标是最小化成本函数。然而，当 $\lambda$ ?的值较大时，正则化项的影响变得更加显著。这可能导致在最小化成本函数的过程中，为了减小正则化项的影响，模型更倾向于减小回归平方和（SSR）部分。这就是为什么在岭回归中，相较于普通线性回归，SSE 可能会变大的原因。

【SST = SSR + SSE

$\text{SSE} = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2$ ? $\text{SST} = \sum_{i=1}^{n} (y_i - \bar{y})^2$ ? ?? $\text{SSR} = \sum_{i=1}^{n} (\hat{y}_i - \bar{y})^2$ 】

具体地说，当 $\lambda$ 较大时，模型更倾向于选择较小的系数值，以便在考虑回归平方和和正则化项时找到一个平衡。这种情况下，虽然回归平方和可能会略微增加，但整体的成本函数可能会更小，从而提高了模型对未见数据的泛化能力。这是正则化方法的一种典型效果，它有助于防止过拟合，即在训练数据上过度拟合，而在新数据上表现不佳。

7.5 用岭回归选择变量

文章来源:https://blog.csdn.net/qq_64279967/article/details/135209168
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：veading@qq.com进行投诉反馈，一经查实，立即删除！