安徽某高校《R语言与统计建模》期末上机题复习

考点1 一元线性回归

模板

# 假设我们有以下数据
x <- c(1, 2, 3, 4, 5) # 自变量
y <- c(2, 4, 6, 8, 10) # 因变量

# 使用lm()函数进行线性回归
model <- lm(y ~ x)

# 查看回归分析的结果
summary(model)

例题

两组数据，分别是最大积雪深度X和当年灌溉面积Y，请回答：

X	5.1	3.5	7.1	6.2	8.8	7.8	4.5	5.6	8.0	6.4
Y	1907	1287	2700	2373	3260	3000	1947	2273	3113	2493

（1）画出散点图，判断Y与X是否是线性关系

（2）求出Y关于X的一元线性方程

（3）对方称做显著性检验

（4）观测得今年的数据是X = 7m，给出今年灌溉面积的预测值和相应的区间估计（）

解答：

# 输入数据
X <- c(5.1, 3.5, 7.1, 6.2, 8.8, 7.8, 4.5, 5.6, 8.0, 6.4)
Y <- c(1907, 1287, 2700, 3273, 3260, 3000, 1947, 2273, 3113, 2493)

# 创建数据框
df <- data.frame(X, Y)

# 绘制散点图
plot(df$X, df$Y, main="Scatterplot of Y against X", xlab="X (in meters)", ylab="Y", pch=19)

# 执行一元线性回归
model <- lm(Y ~ X, data=df)

# 添加回归线
abline(model, col="red")

# 输出模型摘要
summary(model)

# 预测X=7时的Y值，并进行区间估计
new_data <- data.frame(X=7)
predict_value <- predict(model, new_data, interval="predict", level=0.95)

# 打印预测值及其95%置信区间
print(predict_value)

（1）

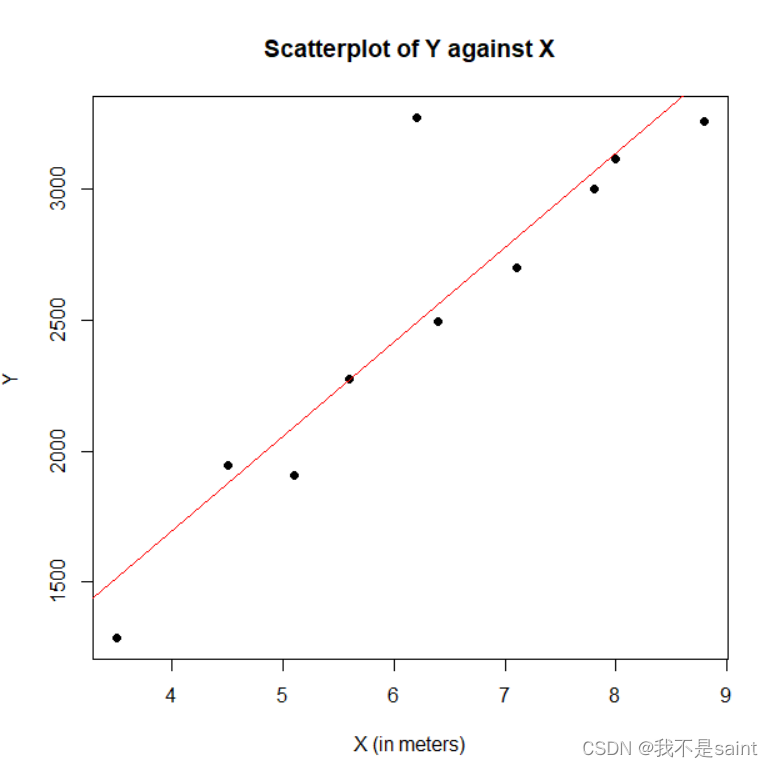
认为有线性关系

（2）

由图中读出 Y=360.59X+253.58

（3）

如结果图，认为检验效果显著

（4）

考点2 单因素方差分析

模板

# 假设我们有以下数据，A, B, 和 C是三个不同的组
group <- rep(c("A", "B", "C"), each=10)
values <- c(rnorm(10, mean=50, sd=10),  # 组A的数据
            rnorm(10, mean=55, sd=10),  # 组B的数据
            rnorm(10, mean=60, sd=10))  # 组C的数据

# 创建数据框
data <- data.frame(group = group, values = values)

# 执行单因素方差分析
anova_result <- aov(values ~ group, data=data)

# 查看方差分析结果
summary(anova_result)

例题

现在有三组数据：

组别	数据
A	115	116	98	83
B	103	107	118	116
C	73	89	85	97

（1）对数据进行方差分析；判断三个组的数值是否有显著差异；

（2）求出每个组数值的均值，做出相应的区间估计（）；

（3）对数据进行多重检验。

解答

# 输入数据
A <- c(115, 116, 98, 83)
B <- c(103, 107, 118, 116)
C <- c(73, 89, 85, 97)

# 创建数据框
df <- data.frame(
  value = c(A, B, C),
  group = factor(rep(c("A", "B", "C"), each=4))
)

# 进行单因素方差分析
anova_result <- aov(value ~ group, data=df)

# 查看方差分析结果
summary(anova_result)

（1）

认为有显著差异

（2）

# 输入数据
A <- c(115, 116, 98, 83)
B <- c(103, 107, 118, 116)
C <- c(73, 89, 85, 97)

# 对每个组进行均值计算和区间估计
results <- list()

# A组
results$A_mean <- mean(A)
results$A_CI <- t.test(A, conf.level=0.95)$conf.int

# B组
results$B_mean <- mean(B)
results$B_CI <- t.test(B, conf.level=0.95)$conf.int

# C组
results$C_mean <- mean(C)
results$C_CI <- t.test(C, conf.level=0.95)$conf.int

# 打印结果
results

（3）

# 假设我们对每个组进行了t检验并获得了以下p值
p_values <- c(t.test(A)$p.value, t.test(B)$p.value, t.test(C)$p.value)

# 应用Bonferroni校正
p_adjusted <- p.adjust(p_values, method = "bonferroni")

# 打印校正后的p值
p_adjusted

单总体均值检验

# 假设我们有以下样本数据
sample_data <- c(1, 2, 3, 4, 5)

# 已知总体均值
mu0 <- 3

# 执行单样本t检验
t_test_result <- t.test(sample_data, mu = mu0)

# 查看检验结果
t_test_result

如果给定一组数据，而不是一个已知的总体均值，并且需要检验这组数据的均值是否有差异，通常是指检验这组数据的均值是否显著地不同于某个假定的均值。通常，这个假定的均值是零或者某个理论值。如果没有特定的理论值，我们通常会对数据集的均值是否显著地不同于0进行检验。

# 给定的样本数据
sample_data <- c(2.3, 2.9, 3.1, 2.8, 3.2, 3.0, 2.7, 2.6, 2.9, 3.1)

# 执行单样本t检验，检验样本均值是否显著不同于0
t_test_result <- t.test(sample_data)

# 查看检验结果
t_test_result

解线性方程组

在R语言中，解线性方程组可以通过使用基础函数solve()来完成。这个函数可以解决形如 Ax = b 的线性方程组，其中 A 是一个系数矩阵，x 是一个未知数向量，b 是一个常数向量。

假设你有一个线性方程组如下所示：

a11x1 + a12x2 = b1 a21x1 + a22x2 = b2

你可以使用R中的solve()函数来找到x1和x2的值。下面是如何做的：

# 定义系数矩阵A
A <- matrix(c(a11, a12, a21, a22), nrow = 2, byrow = TRUE)

# 定义常数向量b
b <- c(b1, b2)

# 解线性方程组
x <- solve(A, b)

# 输出解
print(x)

如果你有具体的方程组和数值，只需将a11, a12, a21, a22, b1, b2替换为实际的数值即可。

区间估计

在R语言中，进行区间估计通常是基于一定的置信水平来估计一个参数（如均值、比例或差异）的置信区间。最常用的是对均值的区间估计，可以使用t.test()函数来实现。

下面是一个使用R进行均值的95%置信区间估计的基本示例：

# 假设我们有一组数据
data <- c(2, 3, 5, 7, 11, 13, 17)

# 进行均值的区间估计
t_test_result <- t.test(data, conf.level = 0.95)

# 输出结果
t_test_result

binom.test()函数用于对一个二项分布的样本比例进行精确的单样本比例检验。它不依赖于大样本近似，因此适用于任何大小的样本。这个测试可以提供关于成功概率的点估计和置信区间。

假设你想检验一枚硬币是否公平。你抛了10次，其中有7次正面朝上。

result <- binom.test(x = 7, n = 10)
print(result)

var.test()

var.test()函数是用于比较两个独立样本方差的F检验。该测试评估两个正态分布总体的方差是否不同。

group1 <- c(2, 3, 7, 5, 9)
group2 <- c(6, 5, 8, 4, 10)

result <- var.test(group1, group2)
print(result)