【LeetCode每日一题】2807. 在链表中插入最大公约数(模拟+求最大公约数的6中写法)
2024-01-07 17:24:07
2024-1-6
文章目录
2807. 在链表中插入最大公约数
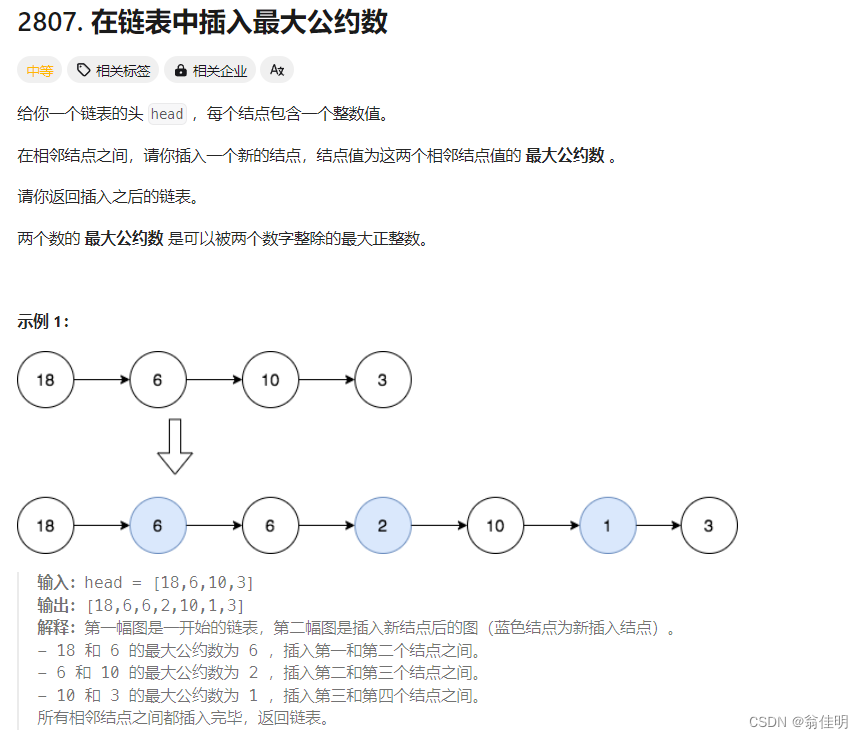
思路:模拟
1.调用函数求出要插入的最大公约数
2.插入到cur的后面
3.因为插了一位,所以移动两个位置
public ListNode insertGreatestCommonDivisors(ListNode head) {
ListNode cur = head;
while (cur.next!=null){
int gcdVal = gcd(cur.val,cur.next.val);
//调用函数求出要插入的最大公约数
cur.next = new ListNode(gcdVal,cur.next);
//插入到cur的后面
cur = cur.next.next;
//因为插了一位,所以移动两个位置
}
return head;
}
/**
* 求两个结点值的最大公约数
* @param a
* @param b
* @return
*/
private int gcd(int a,int b){
//求最大公约数有多种写法
while (a!=0){
int temp = a;
a = b % a;
b = temp;
}
return b;
}
求最大公约数的几种方法:
1.暴力枚举法
public static int gcd(int a, int b) {
int min = a < b ? a : b;//判断并取出两个数中小的数
for (int i = min; i >= 1; i--) { //循环,从最小值开始,依次递减,直到i=1
if (a%i==0&&b%i==0){ //当i能同时被A和B余尽时,返回i
return i;
}
}
return 0;
}
}
2.辗转相除法
public static int gcd(int a, int b) {// 辗转相除法
int c = a % b; //先将a对b取余
while (c != 0) { //当余数不等于0时,一直进行循环,直到余数等于0,公约数就为b
a = b; //将a对b的余数再对b取余,直到循环结束
b = c;
c = a % b;
}
return b;
}
3.辗转相除法 —递归调用
public static int gcd(int a, int b) {// 辗转相除法 改进,调用函数递归
int max = a > b ? a : b; //求出大的数
int min = a < b ? a : b; //求出小的数
if(max%min==0){
return min; //当大数模小数能余尽时,最大公约数就是小的数
}
return gcd(max%min,min);//递归函数,参数去前两个数的余数,和小的数
4.辗转相除法 —递归调用—简化写法
public static int gcd(int a, int b) {// 辗转相除法 改进,调用函数递归
return (a % b == 0) ? b : gcd(b, a%b );// 相同思路,三元运算/简化写法
}
1.如果a余b等于0,说明b就是最大公约数
2.否则,进行递归,b代替曾经的a,让a%b产生的余数代替曾经的b。
3.始终确保大数%小数
4.即使b位置上是值大于a, b代替a后,a(小数)%b(大数) = a ,相当于替换位置
- (b,a%b)的位置不能交换,否则无法跳出递归
5.调用函数递归 更相减损法
public static int gcd(int a, int b) {//调用函数递归 更相减损法
int max = a>b?a:b;
int min = a<b?a:b;
if(max%min==0){
return min;
}
return gcd(max-min,min);//相同思路,将%改为-,优化速度
}
6.调用函数递归 更相减损法–简化
public static int gcd(int a, int b) {//调用函数递归 更相减损法 简易写法
if (a < b) {
int tmp = a;
a = b;
b = tmp;
}
return (a % b == 0) ? b : gcd(a - b, b);
简化不用找大小数,把大数放到前面
因为小数减大数为负数,所以要把大数替换到前面,
public static int gcd5(int a, int b) {//调用函数递归 更相减损法 简易写法
return (a % b == 0) ? b : a > b ? gcd5(a - b, b) : gcd5(b-a,a);
}
压行写法,就是三目嵌套,就是可读性不高

文章来源:https://blog.csdn.net/m0_64003319/article/details/135430305
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!