第 119 场双周赛 + 第 375 场周赛

2959. 关闭分部的可行集合数目

一个公司在全国有?n?个分部，它们之间有的有道路连接。一开始，所有分部通过这些道路两两之间互相可以到达。

公司意识到在分部之间旅行花费了太多时间，所以它们决定关闭一些分部（也可能不关闭任何分部），同时保证剩下的分部之间两两互相可以到达且最远距离不超过?maxDistance?。

两个分部之间的?距离?是通过道路长度之和的?最小值?。

给你整数?n?，maxDistance?和下标从?0?开始的二维整数数组?roads?，其中?roads[i] = [ui, vi, wi]?表示一条从?ui?到?vi?长度为?wi的?无向?道路。

请你返回关闭分部的可行方案数目，满足每个方案里剩余分部之间的最远距离不超过?maxDistance。

注意，关闭一个分部后，与之相连的所有道路不可通行。

注意，两个分部之间可能会有多条道路。

示例 1：

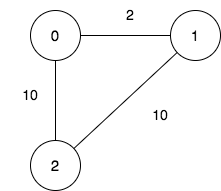
输入：n = 3, maxDistance = 5, roads = [[0,1,2],[1,2,10],[0,2,10]]
输出：5
解释：可行的关闭分部方案有：
- 关闭分部集合 [2] ，剩余分部为 [0,1] ，它们之间的距离为 2 。
- 关闭分部集合 [0,1] ，剩余分部为 [2] 。
- 关闭分部集合 [1,2] ，剩余分部为 [0] 。
- 关闭分部集合 [0,2] ，剩余分部为 [1] 。
- 关闭分部集合 [0,1,2] ，关闭后没有剩余分部。
总共有 5 种可行的关闭方案。

示例 2：

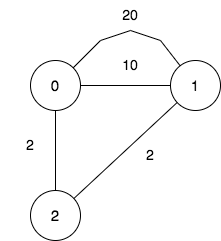
输入：n = 3, maxDistance = 5, roads = [[0,1,20],[0,1,10],[1,2,2],[0,2,2]]
输出：7
解释：可行的关闭分部方案有：
- 关闭分部集合 [] ，剩余分部为 [0,1,2] ，它们之间的最远距离为 4 。
- 关闭分部集合 [0] ，剩余分部为 [1,2] ，它们之间的距离为 2 。
- 关闭分部集合 [1] ，剩余分部为 [0,2] ，它们之间的距离为 2 。
- 关闭分部集合 [0,1] ，剩余分部为 [2] 。
- 关闭分部集合 [1,2] ，剩余分部为 [0] 。
- 关闭分部集合 [0,2] ，剩余分部为 [1] 。
- 关闭分部集合 [0,1,2] ，关闭后没有剩余分部。
总共有 7 种可行的关闭方案。

示例 3：

输入：n = 1, maxDistance = 10, roads = []
输出：2
解释：可行的关闭分部方案有：
- 关闭分部集合 [] ，剩余分部为 [0] 。
- 关闭分部集合 [0] ，关闭后没有剩余分部。
总共有 2 种可行的关闭方案。

解析：由于数据n<10，直接枚举每种情况，用floys算法+状态压缩

class Solution {
public:
    bool check(int s,vector<vector<int>> f,vector<vector<int>> g,int n,int m)
    {
        for(int i = 0;i < n;i++)
        {
            if((s>>i) & 1)
            { // 选那些点
                f[i] =g[i];
            }
        }


        //Floyd 
        for(int k = 0;k < n;k++)
        {
            if(((s>>k)&1) == 0) continue;
            for(int i = 0;i < n;i++)
            {
                if(((s>>i)& 1) == 0) continue;
                for(int j = 0;j < n;j++)
                {
                    f[i][j] = min(f[i][j],f[i][k]+f[k][j]);
                }
            }
        }

        for(int i=0;i <n;i++)
        {
            if(((s>>i)&1) == 0) continue;
            for(int j = 0;j < n;j++)
            {
                if((s>>j)&1 && f[i][j] > m)
                {
                    return false;
                }
            }
        }
        return true;

    }
    int numberOfSets(int n, int maxDistance, vector<vector<int>>& roads) {
        vector<vector<int>> g(n,vector<int>(n,INT_MAX/2));
        for(int i= 0;i <n;i++)
        {
            g[i][i] =0;
        }
        for(auto &e:roads)
        {
            int x = e[0],y =e[1],w = e[2];
            g[x][y] = min(g[x][y],w);
            g[y][x] = min(g[y][x],w);
        }
        vector<vector<int>> f(n);
        int ans = 0;
        for(int s = 0;s < (1<<n);s++)
        {
            ans+= check(s,f,g,n,maxDistance);
        }
        return ans;
    }
};

2963. 统计好分割方案的数目

给你一个下标从?0?开始、由?正整数?组成的数组?nums。

将数组分割成一个或多个?连续?子数组，如果不存在包含了相同数字的两个子数组，则认为是一种?好分割方案?。

返回?nums?的?好分割方案?的?数目。

由于答案可能很大，请返回答案对?109 + 7?取余?的结果。

示例 1：

输入：nums = [1,2,3,4]
输出：8
解释：有 8 种 好分割方案 ：([1], [2], [3], [4]), ([1], [2], [3,4]), ([1], [2,3], [4]), ([1], [2,3,4]), ([1,2], [3], [4]), ([1,2], [3,4]), ([1,2,3], [4]) 和 ([1,2,3,4]) 。

示例 2：

输入：nums = [1,1,1,1]
输出：1
解释：唯一的 好分割方案 是：([1,1,1,1]) 。

示例 3：

输入：nums = [1,2,1,3]
输出：2
解释：有 2 种 好分割方案 ：([1,2,1], [3]) 和 ([1,2,1,3]) 。

提示：

• 1 <= nums.length <= 105
• 1 <= nums[i] <= 109

解析：

记录每个元素相等元素的右端点，这样子就可以变成区间合并问题的，每个区间可以选择合并和不合并。设子区间有m个，则总的合并个数为2^m个。

class Solution {
public:
    int numberOfGoodPartitions(vector<int>& nums) {
        unordered_map<int,pair<int,int>> ps;
        for(int i = 0;i <nums.size();i++)
        {
            int x = nums[i];
            if(ps.find(x) != ps.end())
            {
                ps.find(x)->second.second = i;
            }else{
                ps[x] = {i,i};
            }
        }

        vector<pair<int,int>> a;
        for(const pair<int,pair<int,int>> &p:ps)
        {
            a.emplace_back(p.second);
        }
        sort(a.begin(),a.end(),[](const auto &p,const auto &q)
        {
            return p.first < q.first;
        });
        int ans = 1;
        int max_r = a[0].second;
        for(int i = 1;i < a.size();i++)
        {
            int left = a[i].first,right = a[i].second;
            if(left > max_r)
            {
                ans = ans*2 % 1000000007;
            }
            max_r = max(max_r,right);
        }
        return ans;
    }
};

这里的unordered_map遍历要加const 才可以运行。