K-means聚类模型（超详细，含案例代码）

什么是K-means ?

????????K-means是一种常用的聚类算法，用于将数据集中的观测点分为不同的群组或簇。聚类是一种无监督学习方法，其目标是发现数据中隐藏的结构，将相似的数据点划分为同一组，同时将不相似的数据点划分为不同的组。

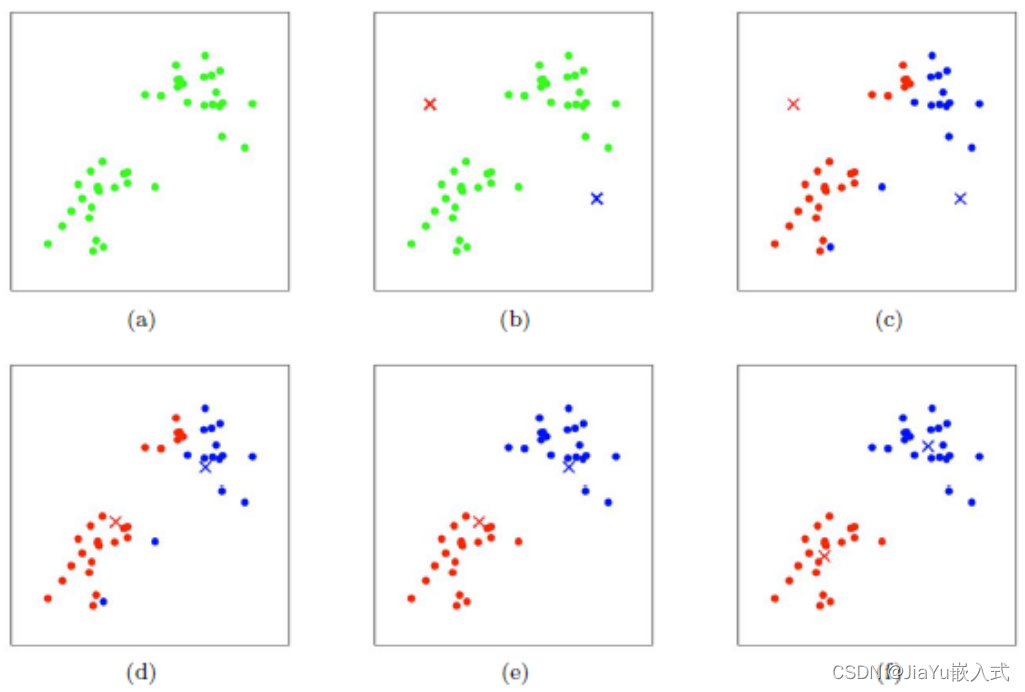
K-means聚类的工作原理

1. ? ? ? ? 1、选择簇的数量（K）： 首先，用户需要指定要将数据分成多少个簇。这通常是在算法应用之前由用户提供的一个参数。
2. ? ? ? ? 2、初始化聚类中心： 随机选择K个数据点作为初始聚类中心（centroid）。这些中心点代表了每个簇的中心。
3. ? ? ? ? 3、分配数据点到最近的聚类中心： 对于每个数据点，计算其与每个聚类中心的距离，将其分配给距离最近的聚类中心所在的簇。
4. ? ? ? ? 4、更新聚类中心： 对于每个簇，计算该簇中所有数据点的平均值，将这个平均值作为新的聚类中心。
5. ? ? ? ? 5、重复步骤3和步骤4： 重复这个过程，直到聚类中心不再发生显著变化，或者达到预定的迭代次数。

????????K-means的目标是最小化簇内的平方误差，即最小化每个数据点到其簇内聚类中心的距离的平方和。虽然K-means在处理大型数据集时效果良好，但它对于初始聚类中心的选择敏感，并且可能陷入局部最小值。因此，通常会多次运行算法，并选择效果最好的一组聚类结果。

什么时候用K-means聚类算法？

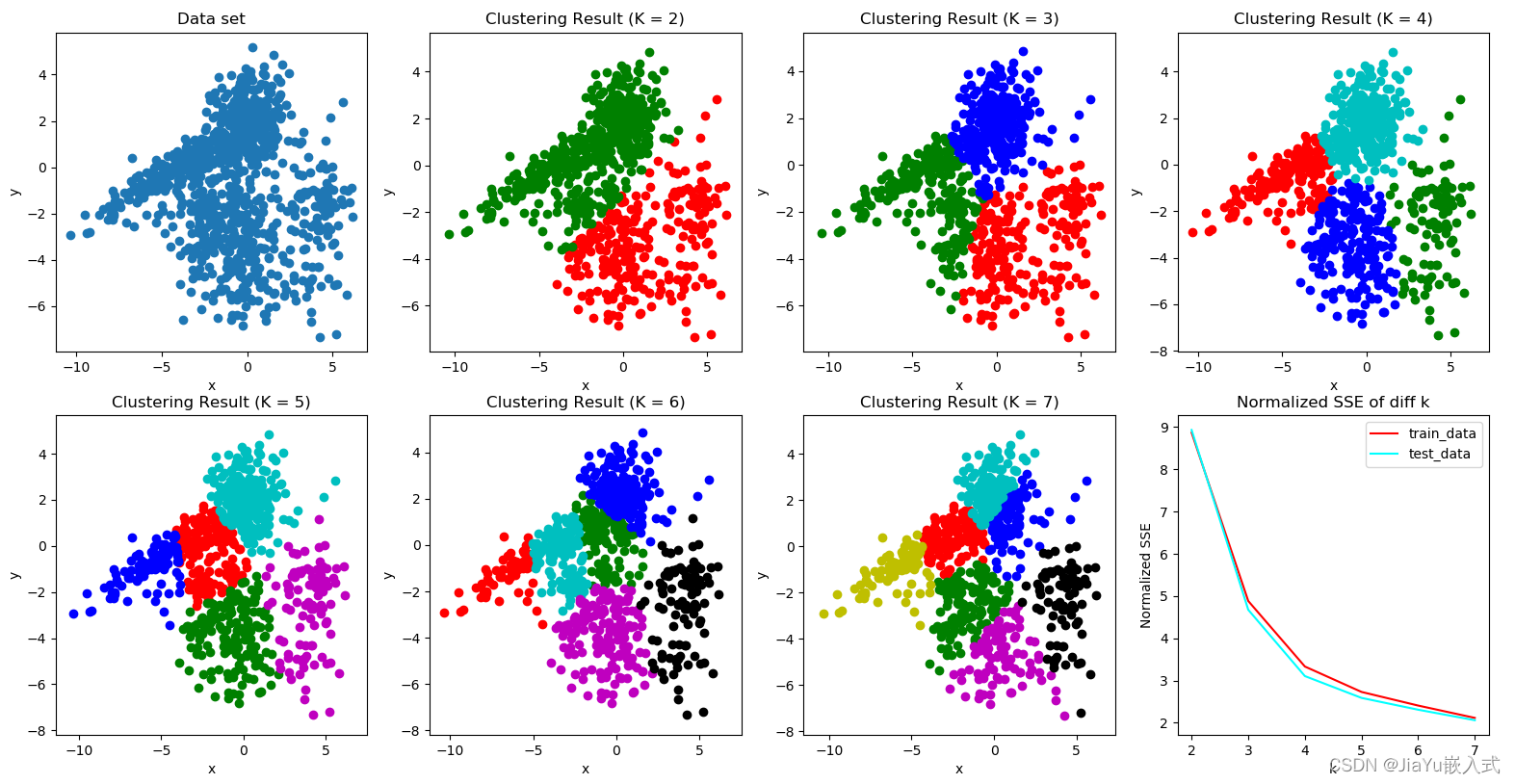
????????数据集中存在自然的群集结构： K-means假设数据可以被分为若干个紧密聚集的群集，适用于数据集中存在簇结构的情况。

????????对计算效率要求较高： K-means是一种计算效率较高的算法，特别是对于大型数据集。它通常是大规模数据集聚类的首选算法之一。

????????簇的形状近似为球形： K-means对于各向同性（球形）簇的效果较好。如果簇的形状非常复杂或者簇之间有重叠，K-means的性能可能会下降。

????????对于划分性质的问题： K-means适用于将数据点划分为互不重叠的簇的问题，每个数据点只属于一个簇。

????????对于初始聚类中心的选择不敏感时： 尽管K-means对于初始聚类中心的选择较为敏感，但在某些情况下，算法的性能可能对初始值不太敏感，或者可以通过多次运行算法以获取不同初始值的结果。

????????注意：K-means并不适用于所有类型的数据和问题。在一些情况下，数据可能不满足K-means的假设，或者聚类的数量不容易确定。在这些情况下，其他聚类算法或深度学习方法可能更为合适。在应用K-means之前，最好先对数据进行探索性分析，确保它满足算法的假设。

案例代码1

????????当使用Python实现K-means聚类时，可以使用一些流行的机器学习库，例如scikit-learn。以下是一个简单的K-means聚类案例代码：

# 导入必要的库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs

# 生成模拟数据
n_samples = 300
n_features = 2
n_clusters = 3

# 使用make_blobs生成聚类数据
X, y = make_blobs(n_samples=n_samples, n_features=n_features, centers=n_clusters, random_state=42)

# 使用KMeans算法进行聚类
kmeans = KMeans(n_clusters=n_clusters)
kmeans.fit(X)

# 获取聚类结果和聚类中心
labels = kmeans.labels_
centers = kmeans.cluster_centers_

# 绘制原始数据和聚类结果
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', edgecolor='k')
plt.scatter(centers[:, 0], centers[:, 1], c='red', marker='X', s=200, label='Centroids')
plt.title('K-means Clustering')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.show()

????????在这个例子中，使用make_blobs生成包含三个簇的模拟数据，然后使用KMeans类进行聚类。最后，我们绘制原始数据和聚类结果，标记出聚类中心。请注意，实际数据可能需要更复杂的预处理和调整参数，具体取决于数据集和应用场景。

案例代码2

????????1.便于理解，首先创建一个明显分为2类20*2的例子（每一列为一个变量共2个变量，每一行为一个样本共20个样本）：

import numpy as np
c1x=np.random.uniform(0.5,1.5,(1,10))
c1y=np.random.uniform(0.5,1.5,(1,10))
c2x=np.random.uniform(3.5,4.5,(1,10))
c2y=np.random.uniform(3.5,4.5,(1,10))
x=np.hstack((c1x,c2x))
y=np.hstack((c2y,c2y))
X=np.vstack((x,y)).T
print(X)

????????2.引用Python库将样本分为两类（k=2），并绘制散点图：

#只需将X修改即可进行其他聚类分析

import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
 
kemans=KMeans(n_clusters=2)
result=kemans.fit_predict(X) #训练及预测
print(result)   #分类结果
 
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei'] #散点图标签可以显示中文
 
x=[i[0] for i in X]
y=[i[1] for i in X]
plt.scatter(x,y,c=result,marker='o')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

结果：
[0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1]

????????3.如果K值未知，可采用肘部法选择K值（假设最大分类数为9类，分别计算分类结果为1-9类的平均离差，离差的提升变化下降最抖时的值为最优聚类数K）

import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist
 
K=range(1,10)
meanDispersions=[]
for k in K:
    kemans=KMeans(n_clusters=k)
    kemans.fit(X)
    #计算平均离差
    m_Disp=sum(np.min(cdist(X,kemans.cluster_centers_,'euclidean'),axis=1))/X.shape[0]
    meanDispersions.append(m_Disp)
 
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei'] #使折线图显示中文
 
plt.plot(K,meanDispersions,'bx-')
plt.xlabel('k')
plt.ylabel('平均离差')
plt.title('用肘部方法选择K值')
plt.show()

案例分析

对某网站500家饭店价格及评论进行聚类

import numpy as np
from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist
import matplotlib.pyplot as plt
import pandas as pd
 
data=pd.read_excel('data.xlsx',header=0).iloc[:501,3:5]
per_25=data.describe().iloc[4,1]
per_75=data.describe().iloc[6,1]
data=data[(data.iloc[:,1]>=per_25)&(data.iloc[:,1]<=per_75)] #选择位于四分位数之内的数
X=np.array(data)
 
 
K=range(1,10)
meanDispersions=[]
for k in K:
    kemans=KMeans(n_clusters=k)
    kemans.fit(X)
    meanDispersions.append(sum(np.min(cdist(X,kemans.cluster_centers_,'euclidean'),axis=1))/X.shape[0])
 
 
 
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.plot(K,meanDispersions,'bx-')
plt.xlabel('k')
plt.ylabel('平均离差')
plt.title('用肘部方法选择K值')
plt.show()

????????具体聚类过程:

from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
 
kemans=KMeans(n_clusters=3)
result=kemans.fit_predict(X)
print(result)
x=[i[0] for i in X]
y=[i[1] for i in X]
plt.scatter(x,y,c=result,marker='o')
plt.xlabel('avgPrice')
plt.ylabel('llCommentNum')
plt.title('对500家饭店价格与评论数进行聚类')

????????聚类结果：

[2 0 0 0 0 1 0 0 2 0 0 2 1 2 0 1 2 0 2 2 2 0 0 0 0 1 2 0 1 0 0 2 2 2 2 2 2
 2 2 0 1 0 0 0 1 0 2 2 0 2 2 0 0 2 2 2 1 0 1 1 1 0 0 0 0 1 2 1 2 0 2 1 0 0
 2 1 1 0 0 1 2 2 0 2 2 1 0 2 1 0 2 0 0 1 0 0 1 1 1 0 0 0 0 0 0 0 0 2 1 2 1
 1 0 0 1 0 1 2 1 0 1 1 0 1 1 0 1 0 2 1 1 0 1 0 2 0 2 1 2 1 1 0 0 1 0 1 0 1
 0 2 0 1 1 0 1 0 0 1 1 1 1 0 0 0 0 1 0 0 0 2 0 1 1 0 1 0 1 0 0 0 0 1 1 0 1
 2 0 1 1 2 0 1 0 0 1 1 1 1 1 0 0 0 1 1 1 2 0 1 1 1 2 2 0 0 2 1 1 2 1 1 1 0
 1 1 0 1 2 2 0 2 2 2 0 1 0 1 1 2 1 1 1 0 1 1 1 1 0 0 0 0 1]