【数据结构】——排序篇（上）

前言：前面我们已经学过了许许多多的排序方法，如冒泡排序，选择排序，堆排序等等，那么我们就来将排序的方法总结一下。

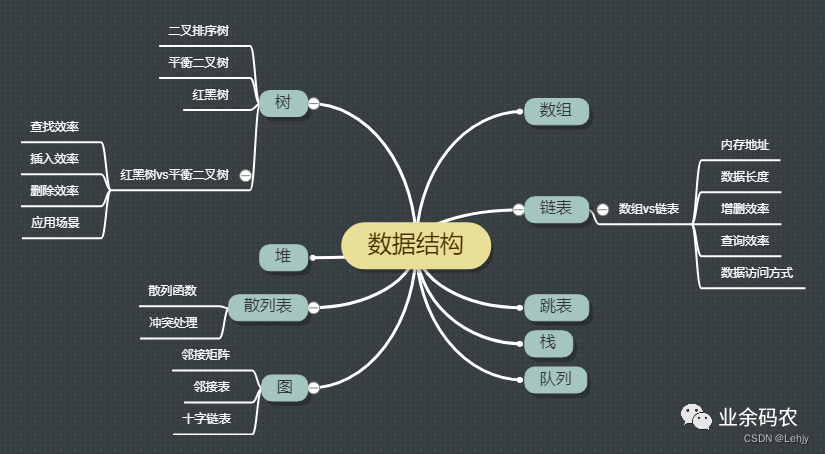
我们的排序方法包括以下几种，而快速排序和归并排序我们后面进行详细的讲解。

直接插入排序：

void InsertSort(int* a, int n)
{
	// [0, end] end+1
	for (int i = 0; i < n - 1; ++i)
	{
		int end = i;
		int tmp = a[end + 1];
		while (end >= 0)
		{
			if (tmp > a[end])
			{
				a[end + 1] = a[end];
				--end;
			}
			else
			{
				break;
			}
		}

		a[end + 1] = tmp;
	}
}

直接插入排序顾名思义把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中，直到所有的记录插入完为止，得到一个新的有序序列 。
我们用一个变量来保存我们插入数据的原数组中的后一个数据，我们排的是降序，那么我们的后一个数据比前一个数据大的话，我们的后一个数据tmp就被前一个覆盖，直到end<0或者我们的后一个数据比前一个小我们就跳出循环，我们保存的数据就等于我们跳出循环的这个数。

希尔排序：

void ShellSort(int* a, int n)
{
	int gap = n;

	// gap > 1时是预排序，目的让他接近有序
	// gap == 1是直接插入排序，目的是让他有序
	while (gap > 1)
	{
		//gap = gap / 2;
		gap = gap / 3 + 1;

		for (int i = 0; i < n - gap; ++i)
		{
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{
				if (tmp < a[end])
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			a[end + gap] = tmp;
		}
	}

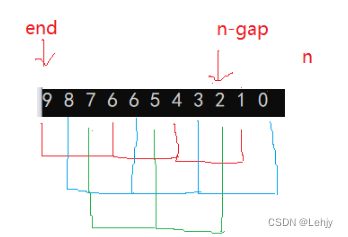
希尔排序的思想是先选定一个整数，把待排序文件中所有记录分成个组，所有距离为的记录分在同一组内，并对每一组内的记录进行排序。然后，取，重复上述分组和排序的工作。当到达=1时，所有记录在统一组内排好序。

我们利用希尔排序法可以将数组分成gap组，gap是我们没组两个树之间的间隔， 如果我们的gap是3时，我们就分成了三组，当gap等于0时，我们的红色这组就进行插入排序，当gap为1时，我们蓝色这组就进行插入排序，当gap为2时，我们绿色这组就进行插入排序，这样我们将完成了第一趟排序。我们要完成整个排序的话，我们就得在嵌套一层循环，我们的gap大于1时就进行预排序，我们的gap为1时就是最后一趟排序，我们的gap无论是几，只要最后gap的值为1我们就完成了排序。

选择排序：

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}
void SelectSort(int* a, int n)
{
	int begin = 0, end = n - 1;

	while (begin < end)
	{
		int mini = begin, maxi = begin;
		for (int i = begin + 1; i <= end; ++i)
		{
			if (a[i] < a[mini])
			{
				mini = i;
			}

			if (a[i] > a[maxi])
			{
				maxi = i;
			}
		}

		Swap(&a[begin], &a[mini]);
		if (maxi == begin)
		{
			maxi = mini;
		}
		Swap(&a[end], &a[maxi]);

		++begin;
		--end;
	}
}

我们这里用两个变量来保存小数和大数的下标，我们的后面循环里的数如果比下标为0的数小的话，小数据mini的下标就是我们比第一个数据小的数据i的坐标，我们排序排的是升序，我们的第一个数就是应该是下标为mini的数据，所以我们将就下标为mini的数据与第一个数据交换，们的后面循环里的数如果比下标为0的数大的话就是存放大数据，下标为maxi，我们就用最后一个数据和下标为maxi的数据交换。如果我们最后循环退出的时候我们的maxi还等于begin，那么我们的下标为begin的数据就是最小的。

堆排序：

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}
void AdjustDown(int* a, int size, int parent)
{
	int child = parent * 2 + 1;

	while (child < size)
	{
		// 假设左孩子小，如果解设错了，更新一下
		if (child + 1 < size && a[child + 1] > a[child])
		{
			++child;
		}

		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

// 升序
void HeapSort(int* a, int n)
{
	// O(N)
	// 建大堆
	for (int i = (n - 1 - 1) / 2; i >= 0; --i)
	{
		AdjustDown(a, n, i);
	}

	// O(N*logN)
	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		--end;
	}
}

我们要排升序，所以我们需要建立一个大堆，大堆的特点是子节点大于根节点，我们通过不断将根节点和最后一个节点交换，进行向下调整，我们的数据大的节点就会沉在底下，而小的节点就会浮在上面，最后我们通过遍历就能够输出升序的数据。

冒泡排序：

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}
void BubbleSort(int* a, int n)
{
	for (int j = 0; j < n; j++)
	{
		bool exchange = false;
		for (int i = 1; i < n - j; i++)
		{
			if (a[i - 1] > a[i])
			{
				Swap(&a[i - 1], &a[i]);
				exchange = true;
			}
		}

		if (exchange == false)
			break;
	}

冒泡排序我们很早之前就已经了解过了，我这里就不多赘述了，如果有疑问的话就看我之前的文章
https://blog.csdn.net/Lehjy/article/details/132266676，相信以你的聪明才智一定可以完美的解决。

最后感谢大家一如既往的支持！谢谢大家！