机器学习 | 聚类Clustering 算法
??????? 物以类聚人以群分。
??????? 什么是聚类呢?
????????
1、核心思想和原理
聚类的目的
????????同簇高相似度
????????不同簇高相异度
????????同类尽量相聚
????????不同类尽量分离
????????
聚类和分类的区别
????????分类 classification
????????????????监督学习
????????????????训练获得分类器
????????????????预测未知数据
????????聚类 clustering
????????????????无监督学习,不关心类别标签
????????????????没有训练过程
??????????????? 算法自己要根据定义的规则将相似的样本划分到一起,不相似的样本分成不同的类别,不同的簇
簇 Cluster
??????? 簇内样本之间的距离,或样本点在数据空间的密度
??????? 对簇的不同定义可以得到不同的算法
????????
主要聚类方法
????????
聚类步骤
- 数据准备:特征的标准化和降维
- 特征选择:最有效特征,并将其存储在向量当中
- 特征提取:特征转换,通过对选择的特征进行一些转换,形成更突出的特征
- 聚类:基于某种距离做相似度度量,得到簇
- 结果评估:分析聚类结果
2、K-means和分层聚类
2.1、基于划分的聚类方式
??????? 将对象划分为互斥的簇
????????每个对象仅属于一个簇
????????簇间相似性低,簇内相似性高
K-均值分类
????????根据样本点与簇质心距离判定
????????以样本间距离衡量簇内相似度
??????? 回顾一下
????????
??????? K均值聚类算法步骤:
- 选择k个初始质心,初始质心的选择是随机的,每一个质心是一个类
- 计算样本到各个质心欧式距离,归入最近的簇
- 计算新簇的质心,重复2 3,直到质心不再发生变化或者达到最大迭代次数
2.2、层次聚类
????????按照层次把数据划分到不同层的簇,形成树状结构,可以揭示数据间的分层结构
????????在树形结构上不同层次划分可以得到不同粒度的聚类
????????过程分为自底向上的聚合聚类和自顶向下的分裂聚类
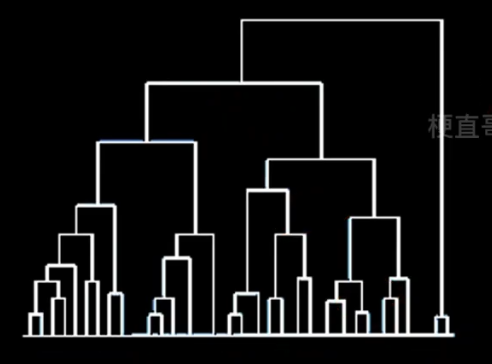
自底向上的聚合聚类
??????? 将每个样本看做一个簇,初始状态下簇的数目 = 样本的数目
??????? 簇间距离最小的相似簇合并
??????? 下图纵轴不是合并的次序,而是合并的距离
????????
??????? 簇间距离(簇间相似度)的度量
??????????????? 第一种 即使已经离得很近,可能也老死不能合并。
??????????????? 第二种 可能出现 链条式 的效果。
??????????????? 第三种 相对合适。
????????????????
????????
?自顶向下的分裂聚类
??????? 所有样本看成一个簇
??????? 逐渐分裂成更小的簇
??????? 目前大多数聚类算法使用的都是自底向上的聚合聚类方法
?3、聚类算法代码实现
import numpy as np
import matplotlib.pyplot as pltfrom sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=250, centers=5, n_features=2, random_state=0)
plt.scatter(X[:,0], X[:,1], c=y)
plt.show()
plt.scatter(X[:,0], X[:,1])
plt.show()
KMeans 聚类法
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=5, random_state=0).fit(X)此处设定簇的个数为5
kmeans.labels_注意,聚类不是分类,0-4只是相当于五个小组,治愈每个组是什么类型并不知道。
array([4, 4, 0, 1, 2, 0, 1, 0, 3, 2, 4, 0, 3, 2, 1, 2, 2, 4, 2, 0, 0, 0,
4, 1, 1, 1, 0, 3, 4, 1, 0, 0, 2, 3, 4, 2, 2, 4, 2, 2, 4, 3, 1, 0,
0, 3, 3, 2, 0, 1, 0, 1, 1, 1, 3, 2, 3, 4, 0, 0, 0, 3, 2, 3, 3, 0,
4, 3, 4, 0, 0, 2, 4, 2, 1, 0, 2, 1, 1, 4, 1, 4, 0, 3, 2, 0, 3, 4,
2, 3, 0, 3, 1, 0, 4, 1, 3, 2, 0, 2, 4, 3, 2, 0, 3, 3, 0, 4, 3, 0,
0, 3, 3, 1, 3, 1, 0, 2, 3, 4, 4, 0, 2, 4, 3, 3, 4, 2, 2, 3, 4, 4,
0, 2, 2, 4, 0, 1, 3, 3, 2, 0, 2, 1, 2, 3, 2, 0, 4, 0, 1, 0, 4, 3,
1, 3, 3, 1, 3, 2, 2, 1, 1, 0, 1, 4, 0, 1, 2, 3, 3, 4, 2, 2, 0, 4,
4, 1, 4, 2, 1, 3, 1, 1, 0, 4, 3, 1, 2, 1, 1, 2, 3, 4, 4, 2, 1, 2,
1, 3, 4, 2, 1, 1, 1, 4, 3, 2, 0, 4, 3, 3, 2, 0, 3, 4, 4, 0, 3, 4,
3, 2, 0, 1, 3, 3, 0, 0, 2, 2, 0, 2, 2, 1, 0, 1, 1, 4, 4, 1, 2, 1,
4, 1, 4, 3, 4, 3, 1, 1], dtype=int32)
plt.scatter(X[:,0], X[:,1], c=kmeans.labels_)<matplotlib.collections.PathCollection at 0x7f3285fb57c0>

center = kmeans.cluster_centers_
centerarray([[ 0.93226669, 4.273606 ],
[ 9.27996402, -2.3764533 ],
[ 2.05849588, 0.9767519 ],
[-1.39550161, 7.57857088],
[-1.85199006, 2.98013351]])
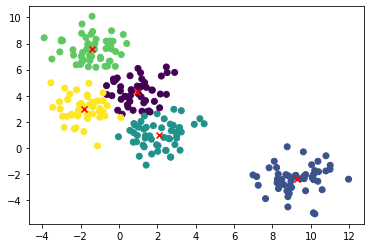
plt.scatter(X[:,0], X[:,1], c=kmeans.labels_)
center = kmeans.cluster_centers_
plt.scatter(center[:,0],center[:,1], marker='x', c = 'red')
plt.show()
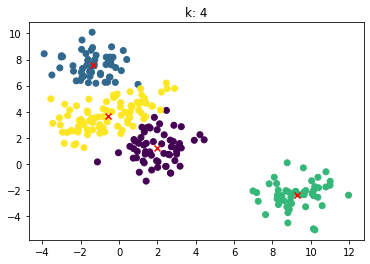
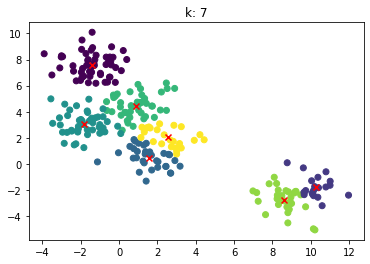
for n_clusters in [2, 3, 4, 5, 6, 7]:
clusterer = KMeans(n_clusters=n_clusters, random_state=0).fit(X)
z = clusterer.labels_
center = clusterer.cluster_centers_
plt.scatter(X[:,0], X[:,1], c=z)
plt.scatter(center[:,0], center[:,1],marker = 'x', c='red')
plt.title("k: {0}".format(n_clusters))
plt.show()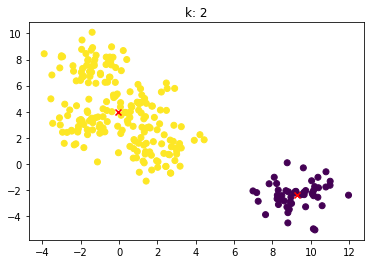



层次聚类法 没有聚类中心
from sklearn.cluster import AgglomerativeClustering
agg = AgglomerativeClustering(linkage='ward', n_clusters=5).fit(X)plt.scatter(X[:,0], X[:,1], c=agg.labels_)
plt.show()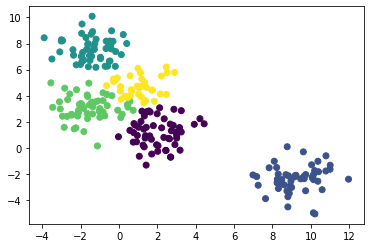
当我们对簇的个数没有预期时,不要一个一个试,可以传入距离的阈值。
agg = AgglomerativeClustering(distance_threshold=10, n_clusters=None).fit(X)
plt.scatter(X[:,0], X[:,1], c=agg.labels_)
plt.show()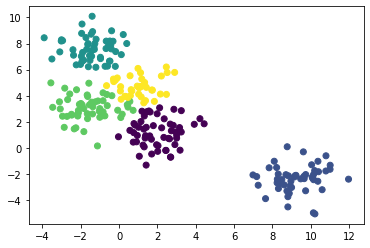
from scipy.cluster.hierarchy import linkage, dendrogram
def show_dendrogram(model):
counts = np.zeros(model.children_.shape[0])
n_samples = len(model.labels_)
for i, merge in enumerate(model.children_):
current_count = 0
for child_idx in merge:
if child_idx < n_samples:
current_count += 1 # leaf node
else:
current_count += counts[child_idx - n_samples]
counts[i] = current_count
linkage_matrix = np.column_stack(
[model.children_, model.distances_, counts]
).astype(float)
dendrogram(linkage_matrix)show_dendrogram(agg)
import time
import warnings
from sklearn import cluster, datasets
from sklearn.preprocessing import StandardScaler
from itertools import cycle, islice
n_samples = 1500
noisy_circles = datasets.make_circles(n_samples=n_samples, factor=0.5, noise=0.05)
noisy_moons = datasets.make_moons(n_samples=n_samples, noise=0.05)
blobs = datasets.make_blobs(n_samples=n_samples, random_state=8)
no_structure = np.random.rand(n_samples, 2), None
# Anisotropicly distributed data
random_state = 170
X, y = datasets.make_blobs(n_samples=n_samples, random_state=random_state)
transformation = [[0.6, -0.6], [-0.4, 0.8]]
X_aniso = np.dot(X, transformation)
aniso = (X_aniso, y)
# blobs with varied variances
varied = datasets.make_blobs(
n_samples=n_samples, cluster_std=[1.0, 2.5, 0.5], random_state=random_state
)
# Set up cluster parameters
plt.figure(figsize=(9 * 1.3 + 2, 14.5))
plt.subplots_adjust(
left=0.02, right=0.98, bottom=0.001, top=0.96, wspace=0.05, hspace=0.01
)
plot_num = 1
default_base = {"n_neighbors": 10, "n_clusters": 3}
datasets = [
(noisy_circles, {"n_clusters": 2}),
(noisy_moons, {"n_clusters": 2}),
(varied, {"n_neighbors": 2}),
(aniso, {"n_neighbors": 2}),
(blobs, {}),
(no_structure, {}),
]
for i_dataset, (dataset, algo_params) in enumerate(datasets):
# update parameters with dataset-specific values
params = default_base.copy()
params.update(algo_params)
X, y = dataset
# normalize dataset for easier parameter selection
X = StandardScaler().fit_transform(X)
# ============
# Create cluster objects
# ============
ward = cluster.AgglomerativeClustering(
n_clusters=params["n_clusters"], linkage="ward"
)
complete = cluster.AgglomerativeClustering(
n_clusters=params["n_clusters"], linkage="complete"
)
average = cluster.AgglomerativeClustering(
n_clusters=params["n_clusters"], linkage="average"
)
single = cluster.AgglomerativeClustering(
n_clusters=params["n_clusters"], linkage="single"
)
clustering_algorithms = (
("Single Linkage", single),
("Average Linkage", average),
("Complete Linkage", complete),
("Ward Linkage", ward),
)
for name, algorithm in clustering_algorithms:
t0 = time.time()
# catch warnings related to kneighbors_graph
with warnings.catch_warnings():
warnings.filterwarnings(
"ignore",
message="the number of connected components of the "
+ "connectivity matrix is [0-9]{1,2}"
+ " > 1. Completing it to avoid stopping the tree early.",
category=UserWarning,
)
algorithm.fit(X)
t1 = time.time()
if hasattr(algorithm, "labels_"):
y_pred = algorithm.labels_.astype(int)
else:
y_pred = algorithm.predict(X)
plt.subplot(len(datasets), len(clustering_algorithms), plot_num)
if i_dataset == 0:
plt.title(name, size=18)
colors = np.array(
list(
islice(
cycle(
[
"#377eb8",
"#ff7f00",
"#4daf4a",
"#f781bf",
"#a65628",
"#984ea3",
"#999999",
"#e41a1c",
"#dede00",
]
),
int(max(y_pred) + 1),
)
)
)
plt.scatter(X[:, 0], X[:, 1], s=10, color=colors[y_pred])
plt.xlim(-2.5, 2.5)
plt.ylim(-2.5, 2.5)
plt.xticks(())
plt.yticks(())
plt.text(
0.99,
0.01,
("%.2fs" % (t1 - t0)).lstrip("0"),
transform=plt.gca().transAxes,
size=15,
horizontalalignment="right",
)
plot_num += 1
plt.show()
4、聚类评估代码实现
聚类效果评估方法
??????? 已知标签评价
????????????????调整兰德指数Adjusted Rand lndex
????????????????调整互信息分Adjusted mutual info score
??????????????????????? 基于预测簇向量与真实簇向量的互信息分数
???????????????? V-Measure
??????????????????????? 同质性和完整性的调和平均值
??????????????? ————取值在-1到1,越接近1越好
????????未知标签评价
????????????????轮廓系数
??????????????????????? 通过计算样本与所在簇中其他样本的相似度
????????????????CHI (Calinski-Harabaz lndex/Variance Ratio Criterion)
??????????????????????? 群间离散度和群内离散度的比例
代码实现
import numpy as np
import matplotlib.pyplot as pltfrom sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=250, n_features=2, centers=5, random_state=0)from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=5, random_state=0).fit(X)
z = kmeans.labels_center = kmeans.cluster_centers_
plt.scatter(X[:,0], X[:,1], c=z)
plt.scatter(center[:,0], center[:,1], marker = 'x', c='red')
plt.show()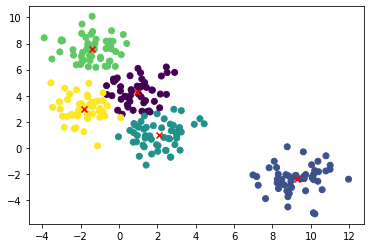
已知标签
from sklearn.metrics import adjusted_rand_score
adjusted_rand_score(y,z)0.8676297613641788
from sklearn.metrics import adjusted_mutual_info_score
adjusted_mutual_info_score(y,z)0.8579576361507845
from sklearn.metrics import v_measure_score
v_measure_score(y,z)0.8608558483955058
ari_curve = []
ami_curve = []
vm_curve = []
clus = [2, 3, 4, 5, 6, 7]
for n_clusters in clus:
clusterer = KMeans(n_clusters=n_clusters, random_state=0).fit(X)
z = clusterer.labels_
ari_curve.append(adjusted_rand_score(y,z))
ami_curve.append(adjusted_mutual_info_score(y,z))
vm_curve.append(v_measure_score(y,z))
plt.plot(clus, ari_curve, label='ari')
plt.plot(clus, ami_curve, label='ami')
plt.plot(clus, vm_curve, label='vm')
plt.legend()
plt.show()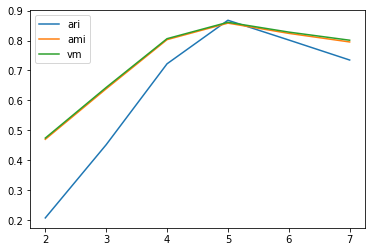
未知标签
from sklearn.metrics import silhouette_score
kmeans = KMeans(n_clusters=5, random_state=0).fit(X)
cluster_labels = kmeans.labels_
si = silhouette_score(X, cluster_labels)
si0.5526930597314647
from sklearn.metrics import silhouette_samples
import matplotlib.cm as cm
def show_silhouette_plot(model, X):
for n_clusters in [2, 3, 4, 5, 6, 7]:
fig, (pic1, pic2) = plt.subplots(1, 2)
fig.set_size_inches(15, 5)
model.n_clusters = n_clusters
clusterer = model.fit(X)
cluster_labels = clusterer.labels_
centers = clusterer.cluster_centers_
silhouette_avg = silhouette_score(X, cluster_labels)
sample_silhouette_values = silhouette_samples(X, cluster_labels)
y_lower = 1
for i in range(n_clusters):
ith_cluster_silhouette_values = sample_silhouette_values[cluster_labels == i]
ith_cluster_silhouette_values.sort()
size_cluster_i = ith_cluster_silhouette_values.shape[0]
y_upper = y_lower + size_cluster_i
color = cm.nipy_spectral(float(i) / n_clusters)
pic1.fill_betweenx(np.arange(y_lower, y_upper), ith_cluster_silhouette_values, facecolor = color)
pic1.text(-0.02, y_lower + 0.5 * size_cluster_i, str(i))
y_lower = y_upper + 1
pic1.axvline(x = silhouette_avg, color = 'red', linestyle = "--")
pic1.set_title("score: {0}".format(silhouette_avg))
colors = cm.nipy_spectral(cluster_labels.astype(float) / n_clusters)
pic2.scatter(X[:,0], X[:,1], marker = 'o', c = colors)
pic2.scatter(centers[:, 0], centers[:, 1], marker = 'x', c = 'red', alpha = 1, s = 200)
pic2.set_title("k: {0}".format(n_clusters))show_silhouette_plot(kmeans, X)


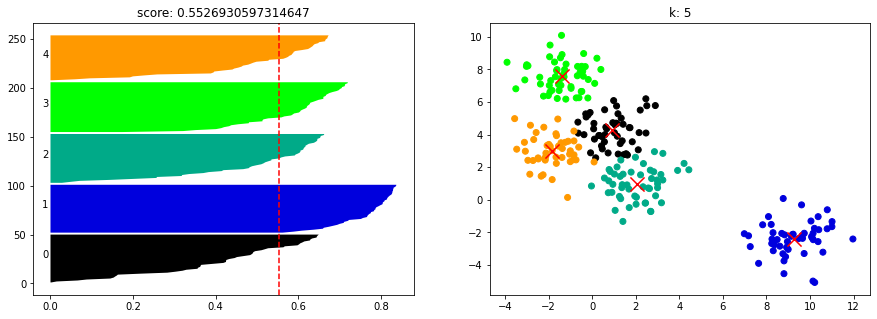


from sklearn.metrics import calinski_harabasz_score
calinski_harabasz_score(X, y)850.6346471314978
chi_curve = []
clus = [2, 3, 4, 5, 6, 7]
for n_clusters in clus:
clusterer = KMeans(n_clusters=n_clusters, random_state=0).fit(X)
z = clusterer.labels_
chi_curve.append(calinski_harabasz_score(X,z))
plt.plot(clus, chi_curve, label='chi')
plt.legend()
plt.show()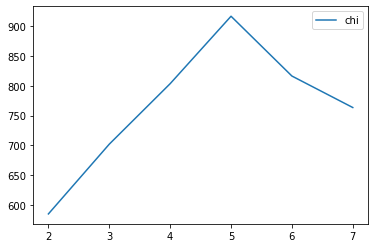
?5、优缺点和适用条件
K--means聚类优缺点
??????? 优点
??????????????? 算法简单,收敛速度快
??????????????? 簇间区别大时效果好
??????????????? 对大数据集,算法可伸缩性强(可伸缩性:但数据从几百上升到几百万时,聚类结果的准确度/一致性 特别好)
??????? 缺点
??????????????? 簇数k难以估计
??????????????? 对初始聚类中心敏感
??????????????? 容易陷入局部最优
??????????????? 簇不规则时,容易对大簇分割(当采用误差平方和的准则作为聚类准则函数,如果各类的大小或形状差距很大时,有可能出现将大类分割的现象)
‘
’K--means聚类适用条件
??????? 簇是密集的、球状或团状
??????? 簇与簇间区别明显
??????? 簇本身数据比较均匀
??????? 适用大数据集
??????? 凸性簇
分层聚类优缺点
??????? 优点
??????????????? 距离相似度容易定义限制少
??????????????? 无需指定簇数
??????????????? 可以发现簇的层次关系
??????? 缺点
??????????????? 由于要计算邻近度矩阵,对时间和空间需求大
??????????????? 困难在于合并或分裂点的选择
??????????????? 可拓展性差
????????????????????
分层聚类适用条件
??????? 适合于小型数据集的聚类
??????? 可以在不同粒度水平上对数据进行探测,发现簇间层次关系
参考
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!