现代雷达车载应用——第3章 MIMO雷达技术 3.2节 汽车MIMO雷达波形正交策略
????????经典著作,值得一读,英文原版下载链接【免费】ModernRadarforAutomotiveApplications资源-CSDN文库。?????
3.2 汽车MIMO雷达波形正交策略
????????基于MIMO雷达技术的汽车雷达虚拟阵列合成依赖于不同天线发射信号的可分离性。当不同天线的发射信号正交时,分离更容易。在下面,我们回顾在传输FMCW时实现波形正交性的技术,例如时分复用(TDM)、多普勒分复用(DDM)和频分复用(FDM)。
3.2.1 通过TDM(实现)波形正交
????????在TDM MIMO雷达中[8-12],每个时隙只安排一个发射天线发射。在图3.3中,NXP半导体给出了时分复用(TDM)条件下MIMO雷达的信号处理示例[13],其中Mt = 2个发射天线交替发射FMCW chirp。发射天线之间的切换延迟为Δt = TPRI,在每个接收天线处,对每个chirp进行长度为Nr的距离FFT,将第2个chirp的FFT输出分别放在奇偶chirp序列对应的两个矩阵中。奇数和偶数chirp序列对应的接收阵列形成两个子阵列,可以根据交错或堆叠的配置合成虚拟阵列。
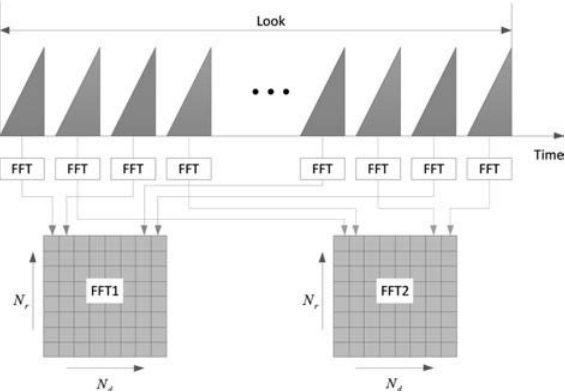
????????图3.3使用TDM体制的雷达信号处理示例,这里Mt=2个发射天线交替发射FMCW chirp序列。红色和绿色分别表示奇数和偶数回波chirp序列。对每个chirp进行距离FFT, FFT输出分别存储在奇数和偶数序列对应的两个矩阵中,以供进一步处理[6]。
?????? 对于一个速度为v的运动目标,发射天线的切换延迟导致目标相位从一个chirp到另一个chirp的偏移,被定义为![]() 。因此,虚拟阵列方向图将被扭曲[10]。在图3.3,两个矩阵中对应列之间的相位差为
。因此,虚拟阵列方向图将被扭曲[10]。在图3.3,两个矩阵中对应列之间的相位差为![]() 。如果v=-0.5Vmax、v=-Vmax,这里Vmax是最大不模糊可探测径向速度,并且
。如果v=-0.5Vmax、v=-Vmax,这里Vmax是最大不模糊可探测径向速度,并且![]() ,对应的相移为φ=-π/2、φ=-π。图3.4展示了移动目标距离为35 m,方位角θ=0°时阵列波束方向图扭曲情况[10]。这里,Mt = 2, Mr = 8的MIMO雷达以时分复用(TDM)方式工作。如文献10和图3.4所示,对于交错MIMO阵列配置,当目标速度增加时,视场边缘的栅瓣出现,而当v = -Vmax时,目标方向的峰值减小并完全消失。对于堆叠MIMO阵列配置,随着目标速度的增加,峰值略低于视轴,且有反方向的镜像栅瓣。
,对应的相移为φ=-π/2、φ=-π。图3.4展示了移动目标距离为35 m,方位角θ=0°时阵列波束方向图扭曲情况[10]。这里,Mt = 2, Mr = 8的MIMO雷达以时分复用(TDM)方式工作。如文献10和图3.4所示,对于交错MIMO阵列配置,当目标速度增加时,视场边缘的栅瓣出现,而当v = -Vmax时,目标方向的峰值减小并完全消失。对于堆叠MIMO阵列配置,随着目标速度的增加,峰值略低于视轴,且有反方向的镜像栅瓣。
????????在测角之前,需要对虚阵响应中每个运动目标引入的相位偏移进行补偿。基于单个接收天线的2D-FFT或同一子阵的非相干2D-FFT积累对每个目标速度进行估计后,可以得到相移估计![]() 。例如,在图3.3中,由偶chirp得到的子阵波束矢量的相位需要用它们乘以
。例如,在图3.3中,由偶chirp得到的子阵波束矢量的相位需要用它们乘以![]() 进行补偿,而对应于奇chirp的子阵波束矢量的相位保持不变。
进行补偿,而对应于奇chirp的子阵波束矢量的相位保持不变。
????????需要注意的是,在时分多址MIMO雷达中,脉冲重复间隔随着发射天线数Mt的增大而增大。其结果是,最大不模糊可探测速度将减少Mt倍[14]。

????????图3.4 对距离35m、方位角θ=0°单目标使用Mt=2、Mr=8的时分多址体制的MIMO雷达距离和方位图示例。考虑两个MIMO阵列配置,交替(左列)和堆叠(右列)。径向速度为,(a-b)v=-Vmax,(c-d)v=-0.5Vmax,(e-f)v=0[6]。
3.2.2 通过DDM(实现)波形正交
????????一次共发射N个chirp(即脉冲),脉冲重复间隔为TPRI,所有发射天线将其与每个天线不同且在脉冲之间变化的相位码相乘后,同时发射相同的FMCW波形,也就是![]() [15]。为了在第l个接收机处分离第h个发射信号,在距离FFT之后,对对应于同一chirp的所有距离单元进行慢时间多普勒解调。N个chirp的多普勒解调输出被组成一个矢量信号
[15]。为了在第l个接收机处分离第h个发射信号,在距离FFT之后,对对应于同一chirp的所有距离单元进行慢时间多普勒解调。N个chirp的多普勒解调输出被组成一个矢量信号![]() 。然后,对矢量
。然后,对矢量![]() 进行多普勒FFT处理。要在多普勒域中分离发射信号,可以采用以下两种方法中的一种。
进行多普勒FFT处理。要在多普勒域中分离发射信号,可以采用以下两种方法中的一种。
????????第一种方法是设计相位码,使干扰![]() 的多普勒FFT移至高于可检测的最大多普勒频率
的多普勒FFT移至高于可检测的最大多普勒频率![]() 的频率。因此,可以使用低通滤波器(LPF)去除干扰[15]。这种相位代码的一个例子是
的频率。因此,可以使用低通滤波器(LPF)去除干扰[15]。这种相位代码的一个例子是
????????![]() ??(3.3)
??(3.3)
????????其中起始相位αm是跨不同发射天线的线性相位,即: αm=α0m。图3.5a为距离为75 m,速度为10 m/s的目标的距离和多普勒频谱。汽车MIMO雷达有两个发射天线,发射相位码如(3.3)所示,α0 = 1,N= 512。可以看出,来自不同发射天线的信号被转移到更高的多普勒频谱,可以通过多普勒域的LPF去除。在这种方法下,雷达脉冲重复频率![]() 应大于
应大于![]() [16]。因此,如果
[16]。因此,如果![]() 保持不变,则最大可检测的不模糊多普勒频率将降低Mt倍。在实践中,需要开发具有不同外观的不同
保持不变,则最大可检测的不模糊多普勒频率将降低Mt倍。在实践中,需要开发具有不同外观的不同![]() 的多普勒展开或去混叠算法。
的多普勒展开或去混叠算法。
????????第二种方法是设计相位码,使干扰的多普勒FFT以伪噪声的形式分布到整个多普勒频谱中。希望在m = 1,…,Mt时使用离散时间傅里叶变换(DTFT)计算的多普勒频谱[17]中最小化峰值干涉残差(PIR),即:
????????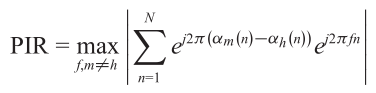 ??(3.4)
??(3.4)
????????这里![]() 。根据(3.4),两个码的频谱的互相关需要是平坦的[17],因为两个码的乘法的傅里叶变换在时域上相当于一个码的频谱与另一个码的时间反转和复共轭的卷积。长度为N的单模序列的最大自相关值为N,两个长度为N的单模序列的理想互相关值为N
。根据(3.4),两个码的频谱的互相关需要是平坦的[17],因为两个码的乘法的傅里叶变换在时域上相当于一个码的频谱与另一个码的时间反转和复共轭的卷积。长度为N的单模序列的最大自相关值为N,两个长度为N的单模序列的理想互相关值为N![]() ,因此,在理想情况下,根据[17],当前传输的信号相对于其他信号的最大功率增益为N
,因此,在理想情况下,根据[17],当前传输的信号相对于其他信号的最大功率增益为N![]() 。例如,对于N= 512的单模序列集,可实现的最大波形衰减约为27.1 dB。
。例如,对于N= 512的单模序列集,可实现的最大波形衰减约为27.1 dB。
????????等幅零自相关码是DDM的良好候选。等幅零自相关码的离散傅立叶变换(DFT)也具有等幅和零自相关[18]。其中一个例子是Chu序列[19],它被定义为![]() ,其中N是素数。在实际中,首先生成素数长度的Chu序列,然后将其截断为一个长度,以便进行有效的FFT。例如,我们生成素数长度为521的Chu码,并将其截断为长度N= 512。通过FFT计算,(3.4)中定义的PIR为1.08N
,其中N是素数。在实际中,首先生成素数长度的Chu序列,然后将其截断为一个长度,以便进行有效的FFT。例如,我们生成素数长度为521的Chu码,并将其截断为长度N= 512。通过FFT计算,(3.4)中定义的PIR为1.08N![]() 。因此,长度N= 512的Chu序列的波形衰减约为26.4 dB。在图3.5b中,我们给出了距离为75 m,速度为10 m/s的目标的距离和多普勒频谱。汽车雷达采用两根发射天线,采用长度为N= 512的两个Chu序列进行慢时间DDM。可以看出,波形衰减约为26 dB。
。因此,长度N= 512的Chu序列的波形衰减约为26.4 dB。在图3.5b中,我们给出了距离为75 m,速度为10 m/s的目标的距离和多普勒频谱。汽车雷达采用两根发射天线,采用长度为N= 512的两个Chu序列进行慢时间DDM。可以看出,波形衰减约为26 dB。
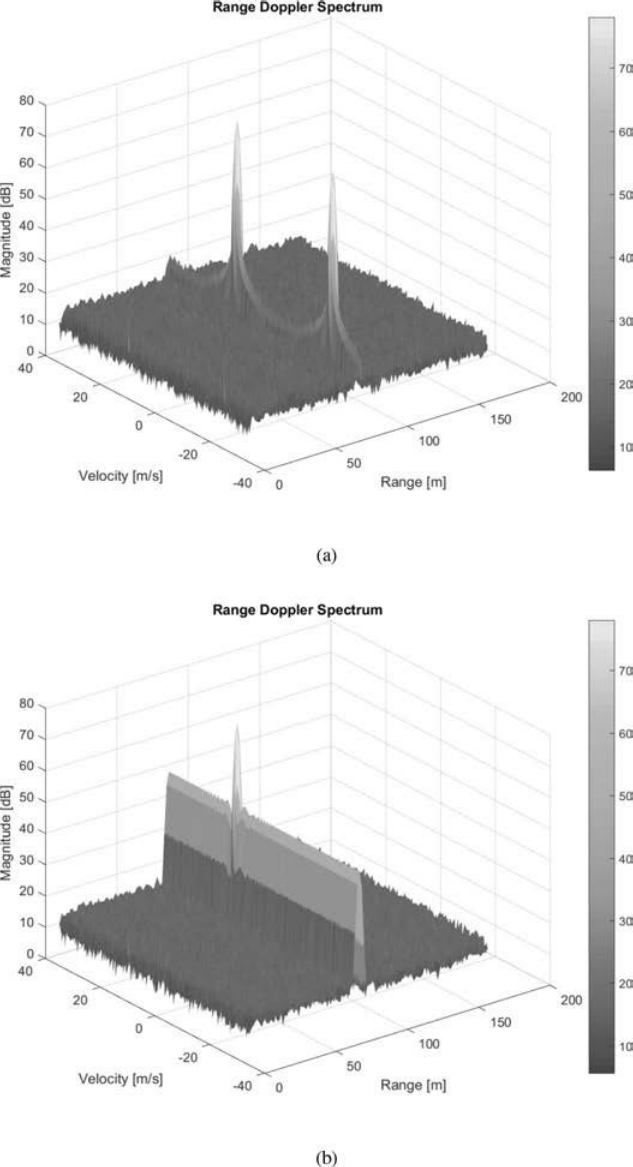
????????图3.5 距离75米、速度为10米/秒的目标的距离和多普勒频谱。车载MIMO雷达有两个发射天线,DDM采用长度为N= 512的慢时间相位编码。(a)(3.3)中定义的相移码。(b)两个楚序列[6]。
?????? 在实际应用中,由于硬件条件的限制,通常采用二进制相位码[20]。通过穷举搜索得到二相码序列,使得(3.4)中的PIR较低。随着代码长度的增加,搜索时间将呈指数增长。
????????慢时间相位编码的好处是来自其他发射机的干扰不会影响不同的距离单元。距离分辨率仅由FMCW chirp的带宽决定。因此,采用快时间相位编码避免了距离旁瓣问题。但是,由于慢时间相位编码的残余,多普勒副瓣会很高。因此,低雷达散射截面积(RCS)目标,如行人,靠近强反射目标,如卡车,可能被波形残差掩盖。也就是说,波形残差减小了雷达的动态范围。在码长给定的情况下,具有良好相关特性的相位码的数量是有限的,也就是说,可以同时发射的天线数量是有限的。
3.2.3 通过FDM(实现)波形正交
????????在FDM体制中,传输的信号由不同的载波频率调制。根据文献[21],通过将第m个发射FMCW chirp偏移一个频偏值![]() 来实现多次发射FMCW信号的分离。如果所有频偏值
来实现多次发射FMCW信号的分离。如果所有频偏值![]() 之间的差值大于抗混叠BPF的截止频率
之间的差值大于抗混叠BPF的截止频率![]() 的两倍,该截止频率由最大不模糊检测距离和多普勒决定,则可以在接收端分离发射信号。具体地说,首先将每个接收机接收到的信号与相同的起始载波频率fc混合。混频器输出中发射信号的分离可以通过移频和频率截止为
的两倍,该截止频率由最大不模糊检测距离和多普勒决定,则可以在接收端分离发射信号。具体地说,首先将每个接收机接收到的信号与相同的起始载波频率fc混合。混频器输出中发射信号的分离可以通过移频和频率截止为![]() 的LPF来实现[21]。每个接收机需要进行Mt次这样的移频滤波操作。因此,使用典型的大带宽FMCW chirp可以实现高距离分辨率。同时,FDM MIMO体制经过FMCW解调、频移和滤波处理后,仍然可以利用由拍频信号决定的低采样率。
的LPF来实现[21]。每个接收机需要进行Mt次这样的移频滤波操作。因此,使用典型的大带宽FMCW chirp可以实现高距离分辨率。同时,FDM MIMO体制经过FMCW解调、频移和滤波处理后,仍然可以利用由拍频信号决定的低采样率。
????????让我们在第2节的示例中考虑FDM体制,即FMCW LRR雷达,最大可探测范围为250米,最大可探测速度为120英里/小时。带宽B = 150mhz,chirp持续时间T= 50s时,最大拍频![]() = 5.0274MHz。因此,在FDM体制中,第m个发射天线的频移可以选择为
= 5.0274MHz。因此,在FDM体制中,第m个发射天线的频移可以选择为![]() = 12(m-1)MHz。中频应该有12Mt MHz的带宽来容纳混频器输出。
= 12(m-1)MHz。中频应该有12Mt MHz的带宽来容纳混频器输出。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!