大数据安全 | 【实验】ElGamal公钥密码
2023-12-15 04:43:39
📚关于ElGamal密码
- ElGamal公钥密码体制是T.ElGamal于1985年提出的,其基本思想正是借用了D-H密钥交换协议的设计思路。
- 基于数据困难问题——离散对数问题
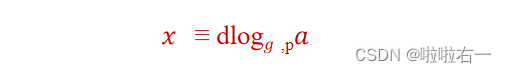
- 具体过程如下:
- 选取一个较大的素数
p,再选取一个本原根g,并将p和g公开; - 随机选取整数a:
1 ≤ a ≤ q-2,并计算出 A = g a A=g^a A=ga,将A作为公开的加密密钥,将a作为保密的脱密密钥。 - 明文:
m, 1 ≤ m ≤p?1


- 选取一个较大的素数
📚实验目的
编程实现ElGamal公钥密码算法。
- 设EIGamal体制的公用素数q=71,其本原根α=7。
- (a)若B的公钥YB=3,A选择的随机整数k=2,则M=30的密文是多少?
- (b)若A选择的k值使得M=30的密文为C=(59,C2),则整数C2是多少?
📚流程梳理
🐇Step1:实现快速幂取模运算
- 实现快速幂取模运算,返回 (base^exp) % mod。
# 实现快速幂取模运算,返回 (base^exp) % mod def mod_exp(base, exp, mod): result = 1 # 将底数取模,防止中间结果过大 base = base % mod while exp > 0: # 当指数大于0时循环 if exp % 2 == 1: # 若指数的当前位为1 result = (result * base) % mod # 将当前的底数乘到结果中,并对模取余 exp = exp // 2 # 将指数右移一位,相当于除以2 base = (base * base) % mod # 底数取平方并对模取余 return result
🐇Step2:求解问题一
# 公用素数q=71,其本原根α=7
q = 71
a = 7
# (a)若B的公钥YB=3,A选择的随机整数k=2,则M=30的密文是?
YB = 3
k = 2
M = 30
print("题一:")
C1 = mod_exp(a, k, q)
C2 = M * mod_exp(YB, k, q) % q
print("若B的公钥YB=3,A选择的随机整数k=2,则M=30的密文为:C=({}, {})".format(C1, C2))
🐇Step3:求解问题二
# (b)若A选择的k值使得M=30的密文为C=(59,C2),则整数C2是?
print("题二:")
C1 = 59
for i in range(1, q - 1):
temp = mod_exp(a, i, q) % q
if temp == C1:
print("此时的随机数k为:", i)
k = i
C2 = M * mod_exp(YB, k, q) % q
print("若A选择的k值使得M=30的密文为C=(59,C2),则整数C2是:",C2)
📚实验结果
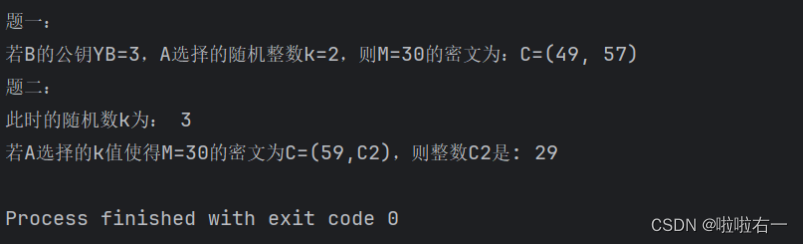
文章来源:https://blog.csdn.net/m0_63398413/article/details/135006296
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!